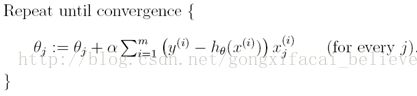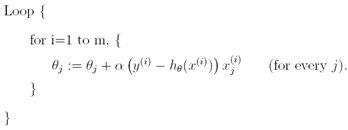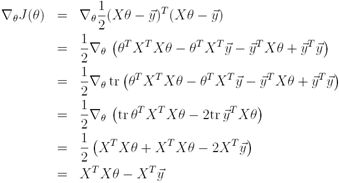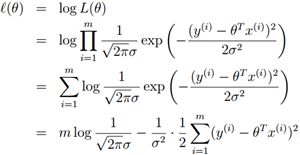【机器学习 吴恩达】CS229课程笔记notes1翻译-Part I线性回归

CS229课程笔记

吴恩达

 

监督学习

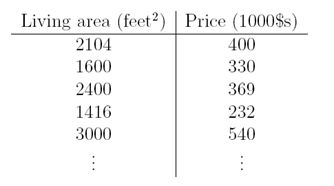
      让我们开始谈论一些监督学习的例子。假定我们有一个数据集，给出俄勒冈州波特兰地区47套房屋的居住面积和价格：

      我们可以在图上画出这些点：

      根据这些数据，我们怎么学习预测波特兰地区其他房屋的价格，看作房屋居住面积大小的函数？

      下面定义几个后面使用的符号，我们使用x⁽ⁱ⁾表示输入变量（例子中的居住面积），也叫做输入特征，y⁽ⁱ⁾表示输出变量或目标变量，例中为我们试图预测的价格。一对（x⁽ⁱ⁾，y⁽ⁱ⁾）叫做训练样本，我们用来学习的数据集（包含m个训练样本，(x⁽ⁱ⁾,y⁽ⁱ⁾),i=1,2,…,m）叫做训练集。注意，符号中的上标(i)仅仅是训练集的索引，与指数无关。我们也使用X代表输入空间，Y代表输出空间，在该例中，X=Y=R。

      为了更加正式地描述监督学习问题，我们的目标是，给定一个训练集，学习函数：XàY，因此h(x)是相应值y的一个好的预测。出于历史原因，函数h叫做假设。我们把这个过程更形象地表示如下：

      当我们试图预测的目标变量是连续的，比如在我们的房屋例子中，我们叫该学习问题是一个回归问题。当y仅取一些离散值时（比如说，给定居住面积，我们想要预测该住宅是一套住宅还是一个公寓），我们称该问题为分类问题。

 

Part I
线性回归

      为了使我们的房屋例子更加有趣，让我们考虑一个更加丰富的数据集，数据集中还包括每个房屋中卧室的数量：

      这里，输入变量是R²中两维的向量。例如，x₁⁽ⁱ⁾是训练集中第i套房屋的居住面积，x₂⁽ⁱ⁾是房屋中卧室的数量。（一般地，当设计学习问题，由你来决定选取哪个特征，因此如果你在波特兰地区收集住房数据，你也会考虑包括其他特征，比如是否有壁炉，卫生间的数量等等。我们之后将讨论更多关于特征选择的话题，但是现在我们采用已经给定的特征。）

      为了实现监督学习，我们必须决定怎么在计算机中表示函数/假设h。作为初始选择，我们估计y为x的线性函数：

      这里，θ_i是参数（也叫做权重），参数化线性函数的空间，该线性函数从X映射到Y。当不会导致混乱时，我们将丢掉h_θ(x)中的θ下标，简单地写为h(x)。为了简化我们的符号，我们使得x₀=1（这是截距项），因此

      上式右边我们将θ和x都看作向量，n是输入变量的个数（不包括x₀）。

      现在，给定一个训练集，我们怎么挑选，或者学习参数θ？一个合理的方法似乎是使得h(x)靠近y，至少对于我们拥有的训练样本是这样。为了对此形式化，我们将定义一个函数，对于每一个θ值，计算h(x⁽ⁱ⁾)对相应的y⁽ⁱ⁾的靠近程度，我们定义代价函数：

      如果你之前见过线性回归，你可能意识到这是熟悉的最小平方代价函数（least-squares cost function），即一般最小平方回归模型（ordinaryleast squares regression model）。不论你之前是否见过，让我们继续，我们将最终显示这是一个更广泛的算法家族的特殊例子。

 

1 LMS算法

      我们想要选择θ来最小化J(θ)。我们使用一个搜索算法，以θ的某个初始值开始，重复改变θ，使得J(θ)更小，直到我们收敛到一个使得J(θ)最小的θ值。特别地，让我们考虑梯度下降算法，以某个初始的θ开始，重复执行更新：

      （对j=0,…,n的所有的值同时执行更新）这里，α叫做学习率，该算法重复地向着J的最陡下降方向走一步。

为了实现该算法，我们必须计算出右边的偏导数。如果我们只有一个训练样本(x,y)，让我们计算偏导数，以便我们可以忽略J的定义中的和。我们有：

      对于一个单独的训练样本，我们给出下面的更新规则：

      该规则叫做LMS更新规则（LMS代表“least meansquares”，最小均方），也叫做Widrow-Hoff学习规则。该规则有一些自然和直观的特性，例如，更新的大小与错误项（y(i)-h_θ(x⁽ⁱ⁾)）成比例。因此，如果我们在训练样本上的预测特别接近真实值y⁽ⁱ⁾，那么我们就不太需要改变参数；相反，如果我们的预测h_θ(x⁽ⁱ⁾)离y⁽ⁱ⁾很远，我们就需要很大幅度地改变参数。

      我们为仅有一个样本的时候推导LMS规则。有两种方式可以修改超过一个样本的训练集。第一个是用下面算法替代它：

      读者可以容易地验证在上面的更新规则中的和正好是（如J最初的定义）。因此，这仅仅是梯度下降关于最初的代价函数J。该方法在每一步关注整个训练集的每一个样本，叫做批梯度下降。注意到，梯度下降有时会陷入局部极小值，对于线性回归，我们提出的优化方法仅有一个全局最小值，没有其他的局部极小值；因此梯度下降总是收敛（假定学习率α不太大）到全局最小值。实际上，J是一个二次凸函数。下面是一个梯度下降的例子，使得二次函数最小。

      上面的椭圆是二次函数的轮廓。上图也示出了梯度下降的轨迹，初始点在(48,30)，图中的×（由直线连起来）标识梯度下降经过的θ的连续值。

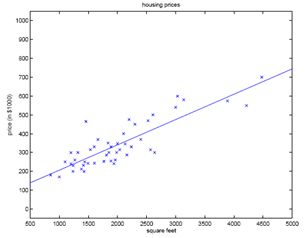
      当我们运行批梯度下降算法在之前的数据集上拟合θ，来学习预测房价，作为居住面积的函数，我们获得θ₀=71.27，θ₁=0.1345,。如果我们描述作为x（面积）的函数，将训练数据描点，会得到下面的图：

      如果卧室的数量也作为一个输入特征，我们得到θ₀=89.60，θ₁=0.1392，θ₂=-8.738。

      上面的结果是通过批梯度下降获得的。有一个批梯度下降算法的替代算法也工作的很好。考虑下面的算法：

      在该算法中，我们重复遍历训练集，每次我们使用一个训练样本更新参数，依据单个训练样本错误梯度。该算法叫做随机梯度下降（也叫做增量梯度下降）。而批梯度下降在走一步之前必须遍历整个训练集——如果m很大，将是一个代价很大的操作——随机梯度下降可以马上行动，并对于它看到的每一个样本持续行动。经常，随机梯度下降得到θ，比批梯度下降更快地靠近最小值。（注意，随机梯度下降算法可能永远不会收敛到最小值，参数θ将一直在最小值J(θ)周围摆动，但实际上绝大多数靠近最小值的值已经十分接近真实的最小值。）因此，当训练集特别大时，随机梯度下降的性能通常超过批梯度下降。

 

2  等式

      梯度下降给出了一种方式最小化J，我们来讨论第二种方式来最小化J，这次我们明确地进行最小化，而不采用迭代算法。在该方法中，我们将通过明确地对θ求导来最小化J，并将导数设置为0。为了不写数组和满页的导数矩阵的计算方法，我们引进一些符号来做矩阵的计算。

 

2.1  矩阵求导

      对于函数f：R^m×n-->R，从m×n的矩阵映射到实数，我们定义f关于A的导数如下：

      因此，梯度是一个m×n的矩阵，其(i,j)元是，例如，假设是一个2×2的矩阵，函数f：R^2×2-->R如下给定：

      这里，A_ij代表矩阵A的(i,j)项，那么，我们有

      我们引进trace操作（求迹），写作“tr”。对于一个n×n的方阵A，A的迹定义为其对角线的和：

      如果a是一个实数（例如，一个1×1的矩阵），那么tra=a。（如果你之前没有见过该操作符，你可以把A的迹看作tr(A)，或者将trace函数应用到矩阵A。然而，我们通常的写法是没有括号。）

      求迹操作有如下特性，对于两个矩阵A和B，AB是方阵，我们有trAB=trBA。其有如下推论：

      trABC = trCAB = trBCA，

      trABCD = trDABC = trCDAB = trBCDA

      下面关于求迹操作的特性容易验证。这里，A和B是方阵，a是一个实数：

      trA = trA^T

      tr(A+B) = trA + trB

      traA = atrA

      我们现在陈述但不证明一些关于矩阵求导的事实。等式（4）仅应用到非奇异方阵A，|A|代表A的行列式。我们有：

      为了使我们的矩阵符号更加具体，我们现在详细解释等式（1）的意义。假定我们有某个给定矩阵B∈R^n×m。我们定义函数f：R^m×n-->R，依据f(A) = trAB。注意该定义是有意义的，因为如果A∈R^m×n，那么AB是一个方阵，我们可以对其应用求迹操作；因此，f实际上从R^m×n映射到R。我们可以应用我们矩阵求导的定义来得到，它是一个m×n矩阵。上面的等式（1）陈述了该矩阵的(i,j)项将如下计算：(i,j)-B^T的相应项，或者相当于，B_ji。

等式（1-3）的证明相当简单，留作给读者的练习。等式（4）可以使用矩阵逆的伴随来推导。

 

2.2  再说最小平方

      拥有矩阵求导工具，我们现在找出最小的J(θ)中的θ，我们开始在矩阵-向量符号中重写J。

      给出一个训练集，定义矩阵X为m×n矩阵（实际是m×n+1，如果我们包括截距项），在行中包含训练样本的输入值：

      为m维的向量，包含所有来自训练集的目标值：

      现在，由于，我们可以容易地验证

      因此，对于向量z，我们有

      最后，为了求J的最小值，我们求J关于θ的导数，结合等式（2）和（3），我们得到，

      因此，

      在第三步，我们运用实数的迹仍然是一个实数的事实；第四步运用trA = trA^T的事实，第五步使用等式（5），其中，AT=θ, B=B^T=X^TX, C=I，和等式（1）。为了最小化J，我们设置其导数为0，获得了等式：

      因此，最小的J(θ)中θ的值表示如下：

 

3  概率解释

      对于回归问题，为什么线性回归，特别为什么最小平方代价函数J，是一个合理的选择？在这一部分，我们将给出一系列概率假设，在这些假设下，可以非常自然地推导出最小平方回归算法。

      让我们假设目标变量和输入通过下面的等式相关：

      其中ε⁽ⁱ⁾是错误项，包括或者未建模的因素（比如是否存在一些特征与预测房价非常相关，但是我们在回归中并没有使用），或者随机噪声。让我们进一步假设ε⁽ⁱ⁾是独立同分布的，依据均值为0、方差为σ²的高斯分布（也叫做正态分布）。我们将该假设写为“ε⁽ⁱ⁾~N(0, σ²)”，ε⁽ⁱ⁾的密度通过下式给出：

      这意味着，

      符号“p(y(i)|x(i);θ)”意味着这是给定x⁽ⁱ⁾的y⁽ⁱ⁾的分布，参数为θ。注意，我们不应该以θ为条件(“p(y⁽ⁱ⁾|x⁽ⁱ⁾,θ)”)，由于θ不是随机变量。我们也可以将y⁽ⁱ⁾的分布写为y⁽ⁱ⁾|x⁽ⁱ⁾;θ~N(θ^Tx⁽ⁱ⁾,σ²)。

      给定X（包含所有的x(i)）和θ，那么y⁽ⁱ⁾的分布是什么？数据的概率通过给出。该值被看作（或许X）的函数，对于固定值θ。当我们希望明确地将其视为θ的函数时，我们将其叫做似然函数：

      注意，ε⁽ⁱ⁾的独立假设（因此也是给定x⁽ⁱ⁾的y⁽ⁱ⁾的独立假设），这也可以被写为

      现在，给定与y(i)和x(i)相关的概率模型，我们对参数θ的最好选择采用什么方式是合理的呢？最大似然原则说的是我们应该选择使得似然函数概率尽可能高的θ，例如，我们应该选择使得L(θ)最大的θ。

      代替最大化L(θ)，我们也可以最大化L(θ)的任何严格递增的函数。特别地，如果我们将最大化L(θ)代替为最大化log似然函数l(θ)，推导将会简单一点：

      因此，最大化l(θ)与下式最小化相同：

      我们可以看出它就是J(θ)，我们最初的最小平方代价函数。

      总结：在前面的概率假设下，最小平方回归相当于寻找θ的最大似然估计。因此这是一个假设集合，在该假设下，最小平方回归可以认为是一个自然的方法，仅仅做的是最大似然估计。（注意，概率假设对于最小平方回归不是必需的过程，也存在其他的自然假设。）

      在我们之前的讨论中，我们最终对θ的选择不依赖于σ²的值，即使σ²的值未知，我们也会得到相同的结果。我们后面会再次用到这个事实，当我们谈论指数家族和生成线性模型。

 

4  局部加权线性回归

      考虑从x∈R到y的预测问题，下面的最左图显示了拟合y=θ₀+θ₁x到一个数据集的结果。我们看到数据并不真正靠近一条直线，因此拟合不是非常好。

      如果我们增加了一个额外的特征x²，用y=θ₀+θ₁x+θ₂x²作拟合，我们将获得该数据一个更好的拟合（见中图）。似乎我们添加越多的特征越好，然而，添加太多的特征未必是一件好事：最右图是拟合5阶多项式的结果。我们看到即使拟合的曲线完美地穿过了数据，我们仍然不认为这是一个非常好的预测，例如，对于不同居住面积(x)的房价的预测(y)。还没有正式定义这些项的意义，我们说左边的图是欠拟合的例子，右边的图是过拟合的例子。（之后的课上，我们将讨论学习理论，我们将规范化这些概念，并更加详细地定义假设好或坏意味着什么）。

      像前面讨论的，像上例中所示，特征的选择对于确保学习算法的好性能十分重要。（当我们谈论模型选择，我们也将看到自动选择一系列特征的算法。）在这一部分，让我们简要谈论局部加权线性回归（LWR， locally weighted linear regression）算法，假设我们有足够的训练数据，使得特征的选择不太严格。这个做法很简单，你可以在作业中探索LWR算法的一些特性。

      在最初的线性回归算法中，为了在一个查询点x做出预测（例如，为了计算h(x)），我们将：

      1.      拟合θ来最小化

      2.      输出θ^Tx

      相反，局部加权线性回归算法这样做：

      1.      拟合θ来最小化

      2.      输出θ^Tx

      这里，w⁽ⁱ⁾是非负权重。直观地，如果对于i的特定值，w⁽ⁱ⁾很大，那么我们挑选θ，试图使得(y⁽ⁱ⁾-θ^Tx⁽ⁱ⁾)²较小，如果w⁽ⁱ⁾较小，在拟合的时候，(y⁽ⁱ⁾-θ^Tx⁽ⁱ⁾)²错误项可以忽略。

      对于权重，一个比较标准的选择是：

      注意，权重依赖于特殊点x，此外，如果|x⁽ⁱ⁾-x|很小，那么w⁽ⁱ⁾接近1；如果|x⁽ⁱ⁾-x|很大，那么w⁽ⁱ⁾很小。因此，θ被选择给出一个更高的权重对靠近查询点x的训练样本。（注意，尽管该权重公式的形式类似于高斯分布的密度函数公式，w⁽ⁱ⁾与高斯公式没有直接的关系，w⁽ⁱ⁾不是随机变量，不是服从正态分布的变量。）参数τ控制着一个训练样本的权重多快从x⁽ⁱ⁾下降x距离；τ叫做带宽参数，你可以在作业中做实验。

      局部加权线性回归是我们看到的第一个非参数算法的例子。我们前面看到的非加权线性回归算法是一个参数的学习算法，因为它有一些固定的有限数量的参数（θ_i）进行数据拟合。一旦我们拟合了θ_i并存储，我们不再需要保存训练数据来做出未来的预测。相反，为了使用局部加权线性回归做出预测，我们需要保存整个的训练集。非参数项指的是我们需要保存大量的数据以便假设h随着训练集的大小线性增长。