简单易学的机器学习算法——受限玻尔兹曼机RBM
受限玻尔兹曼机(Restricted Boltzmann Machine, RBM)是一种基于能量模型的神经网络模型,在Hinton提出针对其的训练算法(对比分歧算法)后,RBM得到了更多的关注,利用RBM的堆叠可以构造出深层的神经网络模型——深度信念网(Deep Belief Net, DBN)。下面简单介绍二值型RBM的主要内容。
一、RBM的网络结构
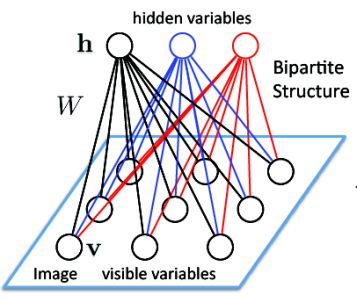
RBM的网络结构如下图所示:
RBM中包括两层,即:
- 可见层(visible layer),图上的 v
- 隐藏层(hidden layer),图上的 h
由上图可知,在同一层中,如上图中的可见层,在可见层中,其节点之间是没有连接的,而在层与层之间,其节点是全连接的,这是RBM最重要的结构特征:层内无连接,层间全连接。
在RBM的模型中,有如下的性质:
当给定可见层神经元的状态时。各隐藏层神经元的之间是否激活是条件独立的;反之也同样成立。
下面给出RBM模型的数学化定义:
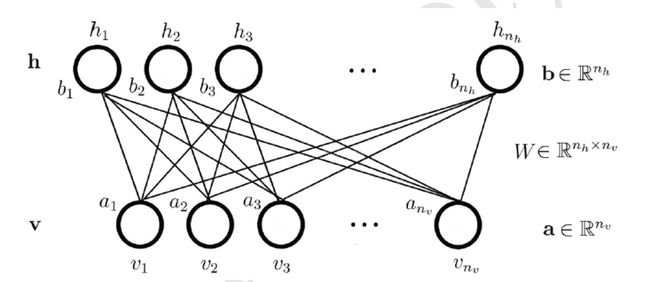
如图:
假设可见层的神经元的个数为 nv ,隐藏层的神经元的个数为 nh , v 表示的是可见层神经元的状态, v=(v1,v2,⋯,vnv)T 。 h 表示的是隐藏层神经元的状态, h=(h1,h2,⋯,hnh)T 。 a 表示的是可见层神经元的偏置, a=(a1,a2,⋯,anv)T∈Rnv 。 b 表示的是隐藏层神经元的偏置, b=(b1,b2,⋯,bnh)T∈Rnh 。 W=(wi,j)∈Rnh×nv 表示的是隐藏层与可见层之间的连接权重。同时,我们记 θ=(W,a,b) 。
二、RBM模型的计算
2.1、能量函数
对于一组给定的状态 (v,h) ,定义如下的能量函数:
利用该能量公式,可以定义如下的联合概率分布:
其中:
称为归一化因子。
当有了联合概率分布,我们便可以定义边缘概率分布,即:
2.2、激活概率
有了上述的联合概率分布以及边缘概率分布,我们需要知道当给定可见层的状态时,隐藏层上的某一个神经元被激活的概率,即 P(hk=1∣v) ,或者当给定了隐藏层的状态时,可见层上的某一神经元被激活的概率,即 P(vk=1∣h) 。
首先定义如下的一些标记:
上式表示的是在 h 中去除了分量 hk 后得到的向量。
有了如上的一些公式,我们可以得到能量公式的如下表示方法:
那么,当给定可见层的状态时,隐藏层上的某一个神经元被激活的概率 P(hk=1∣v) 为:
由Sigmoid函数可知:
则:
同理,可以求得当给定了隐藏层的状态时,可见层上的某一神经元被激活的概率 P(vk=1∣h) :
2.3、模型的训练
2.3.1、模型的优化函数
对于RBM模型,其参数主要是可见层和隐藏层之间的权重,可见层的偏置以及隐藏层的偏置,即 θ=(W,a,b) ,对于给定的训练样本,通过训练得到参数 θ ,使得在该参数下,由RBM表示的概率分布尽可能与训练数据相符合。
假设给定的训练集为:
其中, ns 表示的是训练样本的数目, vi=(vi1,vi2,⋯,vinv)T 。为了能够学习出模型中的参数,我们希望利用模型重构出来的数据能够尽可能与原始数据一致,则训练RBM的目标就是最大化如下的似然函数:
对于如上的似然函数的最大化问题,通常是取其log函数的形式:
2.3.2、最大似然的求解
对于上述的最优化问题,可以使用梯度上升法进行求解,梯度上升法的形式为:
其中, η>0 称为学习率。对于 ∂lnLθ∂θ 的求解,简单的情况,只考虑一个样本的情况,则:
则 ∂lnLθ∂θ 为:
而:
因此上式可以表示为:
其中, ∑hP(h∣v)∂E(v,h)∂θ 表示的是能量梯度函数 ∂E(v,h)∂θ 在条件分布 P(h∣v) 下的期望; ∑v,hP(v,h)∂E(v,h)∂θ 表示的是能量梯度函数 ∂E(v,h)∂θ 在联合分布 P(v,h) 下的期望。
对于 ∑v,hP(v,h)∂E(v,h)∂θ ,可以表示为:
因此,只需要计算 ∑hP(h∣v)∂E(v,h)∂θ ,这部分的计算分为三个,分别为:
- ∑hP(h∣v)∂E(v,h)∂wi,j
- ∑hP(h∣v)∂E(v,h)∂ai
- ∑hP(h∣v)∂E(v,h)∂bj
上述的三个部分计算的方法如下:
已知:
则:
对 wj,i 求导数
∑hP(h∣v)∂E(v,h)∂wj,i=−∑hP(h∣v)hjvi=−∑h∏k=1nhP(hk∣v)hjvi=−∑hP(hj∣v)P(h−j∣v)hjvi=−∑hjP(hj∣v)hjvi∑h−jP(h−j∣v)=−∑hjP(hj∣v)hjvi=−(P(hj=0∣v)⋅0⋅vi+P(hj=1∣v)⋅1⋅vi)=−P(hj=1∣v)vi对 ai 求导数
∑hP(h∣v)∂E(v,h)∂ai=−∑hP(h∣v)vi=−vi∑hP(h∣v)=−vi对 bj 求导数
∑hP(h∣v)∂E(v,h)∂bj=−∑hP(h∣v)hj=−∑h∏k=1nhP(hk∣v)hj=−∑hP(hj∣v)P(h−j∣v)hj=−∑hjP(hj∣v)hj∑h−jP(h−j∣v)=−∑hjP(hj∣v)hj=−(P(hj=0∣v)⋅0+P(hj=1∣v)⋅1)=−P(hj=1∣v)
因此, ∂lnLθ∂θ 为:
2.3.3、优化求解
Hinton提出了高效的训练RBM的算法——对比散度(Contrastive Divergence, CD)算法。
k 步CD算法的具体步骤为:
对 ∀v ,取初始值: v(0):=v ,然后执行 k 步Gibbs采样,其中第 t 步先后执行:
- 利用 P(h∣v(t−1)) 采样出 h(t−1)
- 利用 P(v∣h(t−1)) 采样出 v(t)
上述两个过程分别记为:sample_h_given_v和sample_v_given_h。记 pvj=P(hj=1∣v),j=1,2,⋯,nh ,则sample_h_given_v中的计算可以表示为:
- for j=1,2,⋯,nh do
- {
- 产生 [0,1] 上的随机数 rj
-
hj={10 if rj<pvj otherwise
- }
同样,对于sample_v_given_h,记 phi=P(vi=1∣h),i=1,2,⋯,nv ,则sample_h_given_v中的计算可以表示为:
- for i=1,2,⋯,nv do
- {
- 产生 [0,1] 上的随机数 rj
-
vi={10 if ri<phi otherwise
- }
三、实验
实验代码
# coding:UTF-8
import numpy as np
import random as rd
def load_data(file_name):
data = []
f = open(file_name)
for line in f.readlines():
lines = line.strip().split("\t")
tmp = []
for x in lines:
tmp.append(float(x) / 255.0)
data.append(tmp)
f.close()
return data
def sigmrnd(P):
m, n = np.shape(P)
X = np.mat(np.zeros((m, n)))
P_1 = sigm(P)
for i in xrange(m):
for j in xrange(n):
r = rd.random()
if P_1[i, j] >= r:
X[i, j] = 1
return X
def sigm(P):
return 1.0 / (1 + np.exp(-P))
# step_1: load data
datafile = "b.txt"
data = np.mat(load_data(datafile))
m, n = np.shape(data)
# step_2: initialize
num_epochs = 10
batch_size = 100
input_dim = n
hidden_sz = 100
alpha = 1
momentum = 0.1
W = np.mat(np.zeros((hidden_sz, input_dim)))
vW = np.mat(np.zeros((hidden_sz, input_dim)))
b = np.mat(np.zeros((input_dim, 1)))
vb = np.mat(np.zeros((input_dim, 1)))
c = np.mat(np.zeros((hidden_sz, 1)))
vc = np.mat(np.zeros((hidden_sz, 1)))
# step_3: training
print "Start to train RBM: "
num_batches = int(m / batch_size)
for i in xrange(num_epochs):
kk = np.random.permutation(range(m))
err = 0.0
for j in xrange(num_batches):
batch = data[kk[j * batch_size:(j + 1) * batch_size], ]
v1 = batch
h1 = sigmrnd(np.ones((batch_size, 1)) * c.T + v1 * W.T)
v2 = sigmrnd(np.ones((batch_size, 1)) * b.T + h1 * W)
h2 = sigm(np.ones((batch_size, 1)) * c.T + v2 * W.T)
c1 = h1.T * v1
c2 = h2.T * v2
vW = momentum * vW + alpha * (c1 - c2) / batch_size
vb = momentum * vb + alpha * sum(v1 - v2).T / batch_size
vc = momentum * vc + alpha * sum(h1 - h2).T / batch_size
W = W + vW
b = b + vb
c = c + vc
#cal_err
err_result = v1 - v2
err_1 = 0.0
m_1, n_1 = np.shape(err_result)
for x in xrange(m_1):
for y in xrange(n_1):
err_1 = err_1 + err_result[x, y] ** 2
err = err + err_1 / batch_size
#print i,j,err
print i, err / num_batches
#print W
m_2,n_2 = np.shape(W)
for i in xrange(m_2):
for j in xrange(n_2):
print str(W[i, j]) + " ",
print "\n",
参考文献
- 受限玻尔兹曼机(RBM)学习笔记
- 受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)