人工智能-梯度下降法Python实现

梯度法

什么是梯度

在高数的微积分中,我们学习过对多元函数求偏导,偏导数反映的是函数沿坐标轴方向的变化率,梯度就是偏导数构成的一个向量.

当变化方向与梯度相同或相反时,函数的变化率最大,当变化方向与梯度方向正交时,函数的变化率为0.

∇ f(x,y,z)= (∂ x,∂ y ,∂z) ,每一点的梯度都会因x,y,z的值不一样而变化,因此在每一个点我们都要求一次梯度值.

梯度下降和上升

在机器学习中,我们在求最小值时使用梯度下降法,求最大值时使用梯度上升法.

为了尽快的得到最小值或者最大值,我们尽量让每一步运算的变化率都足够大,因此,在每一次运算时,我们要使函数变化的方向与梯度相同或相反,即△x= ∂ x*A, 这里A是一个常数,也就是步长.

当A为正时,函数变化方向与梯度方向相同,函数增加的最快,当A为负时,函数变化方向与梯度方向相反,函数减少得最快.A数值越大,函数变化得也越快,但A不能太大,过大就有可能因为变化太多错过了最值.

A的最优值往往要在多次尝试后才能确定.

梯度法求二次函数的最小值:

a=0.2 ##迭代精度
## 参数初始值
x1=1
x2=1
all=[0]
X1=[]
X2=[]
##fx函数
def Y(x1,x2):
    return x1*x1+2*x2*x2-4*x1-2*x1*x2
## 各未知数偏导
def dx1(x1,x2):
    return 2*x1-4-2*x2
def dx2(x1,x2):
    return 4*x2-2*x1
##进行梯度下降
def tidu(x1,x2,a):
    temp=Y(x1,x2)
    all.append(temp)
    while(all[-1]-all[-2]!=0):  #当最后两个结果不相等时进入while循环
        a1=x1-dx1(x1,x2)*a     
        a2=x2-dx2(x1,x2)*a
        now=Y(a1,a2)
        x1=a1
        x2=a2
        all.append(now)
        X1.append(x1)
        X2.append(x2)
        
def  main():
    tidu(x1,x2,a)
    print(all)  ##打印所有的f(x)值
    print(X1[-1])  ##打印最小点
    print(X2[-1])
main()
       
   

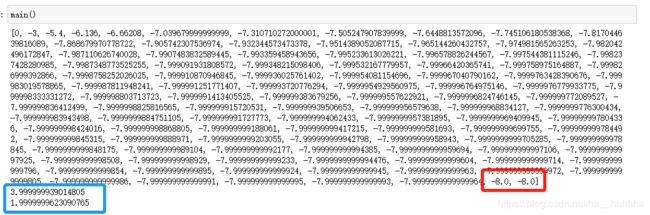
结果如下图,蓝色框住的是最小点,红色是最小值.

店铺多元回归求解系数:

import numpy as np
import random
import math
from sympy import *

## 利用函数求偏导数
x1,x2,b=symbols('x1 x2 b')
y=(469-x1*10-x2*80-b)*(469-x1*10-x2*80-b)
print(diff(y,x1))
print(diff(y,x2))
print(diff(y,b))

##迭代精度
a=0.0000004
##初始值
x1=45##a1
x2=1##a2
x3=70  ##b
area=[10,8,8,5,7,8,7,9,6,9]
distance=[80,0,200,200,300,230,40,0,330,180]
money=[469,366,371,208,246,297,263,436,198,364]

##偏导数
def  dx1(x1,x2,x3):
    S1=0
    for i in range(len(area)):
        S1+=(x3+area[i]*x1+distance[i]*x2-money[i])*20
    return -S1
        
def dx2(x1,x2,x3):
    S2=0
    for i in range(len(area)):
        S2+=(x3+area[i]*x1+x2*distance[i]-money[i])*160
    return -S2
    
def dx3(x1,x2,x3):
    S3=0
    for i in range(len(area)):
        S3+=2*(x3+x1*area[i]+distance[i]*x2-money[i])
    return -S3

##残差
def fx(x1,x2,x3):
    S4=0
    for i in range(len(area)):
        a=money[i]-(x1*area[i]+x2*distance[i]+x3)
        S4+=abs(a)
    return S4
## 梯度下降
all=[0]
x=[]
def  tidu(x1,x2,x3):
    temp=fx(x1,x2,x3)
    all.append(temp)
    while(all[-1]!=all[-2]):
        a1=x1+a*dx1(x1,x2,x3)
        a2=x2+a*dx2(x1,x2,x3)
        a3=x3+a*dx3(x1,x2,x3)
        temp=fx(a1,a2,a3)
        x1=a1
        x2=a2
        x3=a3
        all.append(temp)
    x.append(x1)
    x.append(x2)
    x.append(x3)
    
    
tidu(x1,x2,x3)
print(all)
print(x)

最终结果:

最后的结果与最小二乘法计算出的结果和excel算出来的结果相比还是有很大误差的.