tensorflow 2.0系列（3）：eager execution和计算图

tf 2.0 的新特性：eager execution

tensorflow经典的方式是需要构建计算图，启动会话后，张量在图中流动进行计算。在tf 2.0最大的特色之一就在于eager execution，大大简化了之前这个繁琐的定义和计算过程。

eager execution提供了一种命令式的编程环境，简单地说就是不需要构建图，直接可以运行。在老版本中，需要先构建计算图，然后再执行。在r1.14之后，tensorflow引入了eager execution，为快速搭建和测试算法模型提供了便利。

开启eager模式

tf 2.0 中，默认情况下，Eager Execution 处于启用状态。可以用tf.executing_eargerly()查看Eager Execution当前的启动状态，返回True则是开启，False是关闭。可以用tf.compat.v1.enable_eager_execution()启动eager模式。

import tensorflow.compat.v1 as tf

tf.enable_eager_execution()
print('eager execution ? '+ str(tf.executing_eagerly()))       # => True

x = [[1.]]
m = tf.add(x, x)
print("\nhello, tensorflow r%.1f"%m)  # => "hello, [[4.]]"

关闭eager模式

关闭eager模式的函数是 tf.compat.v1.disable_eager_execution() 。

构建图

graph是tf非常重要的一个概念，在图中定义了整个网络的计算过程，图也对模型做了某种意义上的封装和隔离，使得多个模型可以独立互不影响地运行。首先我们来看看默认图，再看看如何自定义图。

默认图

在tensorflow中，系统会维护一个默认的计算图，通过tf.get_default_graph()函数可以获取当前默认的计算图，计算图中所有的节点都可以视为运算操作op或tensor。在定义好计算图后，tf语句不会立即执行；而是必须等到开启会话session的时候，才会执行session.run()中的语句。如果run中涉及到其他的节点，也会执行到。
通过tf.get_default_graph()函数可以获取当前默认的计算图，为了向默认的计算图中添加一个操作，我们只需要简单的调用一个函数：
** 例1: 默认图 **

c = tf.constant(3.0) 
assert c.graph == tf.get_default_graph() 

with tf.Session(graph=c.graph) as sess:
    print(sess.run(c))

得到输出3.0。

创建多个计算图

还可以用 tf.compat.v1.Graph( ) 函数生成新的计算图。在不同的计算图中，张量和运算都不会共享，彼此是独立的。
** 例2: 创建两个计算图 **

g1 = tf.Graph()
    # 在图g1中定义初始变量c, 并设置初始值为0
    v = tf.get_variable("v", shape=[3], initializer = tf.zeros_initializer(dtype=tf.float32))

g2 = tf.Graph()
with g2.as_default():
    # 在图g1中定义初始变量c, 并设置初始值为1
    v = tf.get_variable("v", shape=[4], initializer = tf.ones_initializer(dtype=tf.float32))

with tf.Session(graph=g1) as sess:
    sess.run(tf.global_variables_initializer())
    with tf.variable_scope('', reuse=True):
        # 输出值为0
        print(sess.run(tf.get_variable("v")))

with tf.Session(graph=g2) as sess:
    sess.run(tf.global_variables_initializer())
    with tf.variable_scope('', reuse=True):
       # 输出值为1
       print(sess.run(tf.get_variable('v')))

输出：

[0. 0. 0.]
[1. 1. 1. 1.]

启动会话

例3: 用tensorflow实现一个累加器，依次输出1，2，3，4，5

import tensorflow.compat.v1 as tf

if ~tf.executing_eagerly():
    tf.disable_eager_execution()
# 逐个输出1，2，3，4，5
# 定义变量节点x，常量节点one，op节点x_new
x = tf.Variable(0, name='counter')  
one = tf.constant(1)
x_new = tf.add(x, one)
# 赋值操作，更新 x
update = tf.assign(x, x_new)

# 计算图初始化
init = tf.initialize_all_variables()
# 启动会话
with tf.Session() as sess:
    sess.run(init)
    for _ in range(5):
        sess.run(update)
        print(sess.run(x))

从公式到计算图

理解了tensor的定义和计算图的构建方法后，我们会发现，其实tensorflow不仅仅是一个神经网络深度学习的算法库，其实也是一个数据流（DFP）的工具。例如在tensorflow中，tensor可以支持各类基本数学计算，构建图可以实现各种函数/方程，用c或者matlab实现的算法都可以用tensorflow实现。我们先举一个简单的例子，绘制心形曲线。

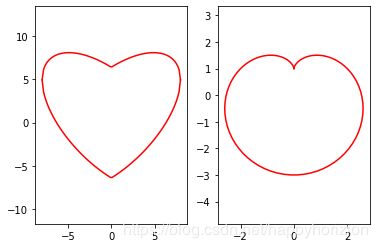
绘制心形曲线

我们试着用两种不同的方法绘制心形曲线。常见的两种心形曲线的公式为：

我们用变量型和占位符型两种方式定义张量，构建tf计算图。

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Mon Jan  6 10:04:01 2020

@author: [email protected]

"""

import tensorflow as tf


if ~tf.compat.v1.executing_eagerly():
    tf.compat.v1.disable_eager_execution()
    
import numpy as np
import matplotlib.pyplot as plt

# 变量型张量   
def variable_tensor(x):

    vx = tf.Variable(x)
    y_part1 = 0.618*tf.math.abs(vx)
    y_part2 = 0.8*tf.math.sqrt(64-tf.math.square(vx))
    
    part1 = tf.math.add(y_part1, y_part2)
    part2 = tf.math.subtract(y_part1, y_part2)
    
    init_op = tf.compat.v1.global_variables_initializer()
    
    with tf.compat.v1.Session() as sess:
        sess.run(init_op)
        y1 = sess.run(part1)
        y2 = sess.run(part2)
    return y1, y2


# 占位符型张量
def placeholder_tensor(data):
    t = tf.compat.v1.placeholder(tf.float32, shape=(100,))
    tx = 2*tf.math.cos(t) - tf.math.cos(2*t)
    ty = 2*tf.math.sin(t) - tf.math.sin(2*t)
    
    with tf.compat.v1.Session() as sess:
        y = sess.run(tx, feed_dict={t:data})
        x = sess.run(ty, feed_dict={t:data})    
    return x,y

if __name__ == "__main__":
    # 心形曲线1
    x = np.linspace(-8,8,100)
    y1, y2 = variable_tensor(x)
    plt.subplot(1,2,1),plt.plot(x, y1, color = 'r')
    plt.subplot(1,2,1),plt.plot(x, y2, color = 'r')
    plt.axis('equal')

    # 心形曲线2
    data = np.linspace(0, 2*np.pi, 100)
    x, y = placeholder_tensor(data)
    plt.subplot(1,2,2),plt.plot(x, y, color = 'r')
    plt.axis('equal')
    plt.show()

得到：

开根号

开根号是一道常见的算法面试题。题目是：给定数字a，在不调用sqrt()函数的情况下求的该数的开方。这道题的经典做法是用牛顿迭代法，当然，也可以用tensorflow来实现（最小二乘法）。

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Mon Jan  6 13:50:45 2020

@author: [email protected]
"""


import tensorflow as tf

if ~tf.compat.v1.executing_eagerly():
    tf.compat.v1.disable_eager_execution()

# 牛顿迭代法
def solve_root(a):  
    x0 = a
    while (x0*x0-a)>1e-5:
        x0 = (x0+a/x0)/2
        
    return x0

# 
def tf_solve_root(a):
    x = tf.Variable(a,dtype=tf.float32)
    x = tf.compat.v1.placeholder(shape=(None,10), dtype=tf.float32)
    x2 = tf.math.multiply(x,x)
    loss = tf.math.square(x2-a)
    opt = tf.compat.v1.train.GradientDescentOptimizer(learning_rate=0.1)
    train = opt.minimize(loss)

    with tf.compat.v1.Session() as sess:
        sess.run(x.initializer)
        for step in range(200):
            sess.run(train, feed_dict={x:a})
            root_a = sess.run(x)
            
    return root_a
            

if __name__=='__main__':
    print(solve_root(2))  
    print(tf_solve_root())
    

得到

1.4142156862745097
1.4142137

线性回归

tensorflow构建线性回归 linear regression model。

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Mon Jan  6 16:15:28 2020

@author: [email protected]
"""

import tensorflow as tf
import numpy as np



if ~tf.compat.v1.executing_eagerly():
    tf.compat.v1.disable_eager_execution()
    
    
x_data = np.random.randn(2000,3)
w_real = [0.4, 0.5, 0.12]
b_real = 0.3

noise = np.random.randn(1,2000)*0.1
y_data = np.matmul(w_real,x_data.transpose())+b_real+noise

NUM_STEPS= 20

g  = tf.Graph()
wb_ = []
with g.as_default():
    x = tf.compat.v1.placeholder(tf.float64, shape=[None, 3])
    y_true = tf.compat.v1.placeholder(tf.float64, shape=None)
    
    w = tf.Variable([[0,0,0]], dtype = tf.float64)
    b = tf.Variable(0, dtype=tf.float64)
    y_pred = tf.matmul(w, tf.transpose(x))+b
    
    loss = tf.reduce_mean(tf.square(y_true-y_pred))
    
    optimizer = tf.compat.v1.train.GradientDescentOptimizer(0.5)
    train = optimizer.minimize(loss)
    
    init = tf.compat.v1.global_variables_initializer()
    with tf.compat.v1.Session() as sess:
        sess.run(init)
        for step in range(NUM_STEPS):
            sess.run(train, {x:x_data, y_true:y_data})
            wb_.append(sess.run([w,b]))
            print(step,sess.run([w,b]))