CS224n笔记1 自然语言处理与深度学习简介
本节课结合了旧版的前半部分(NLP的基本概念的内容)以及新版的绝大多数内容。
0. 本节课程计划
1. NLP的基本概念
1.1 什么是NLP?
NLP是计算机科学、人工智能、语言学的交叉学科。
它的目标是让计算机理解人类语言,从而完成有意义的任务。例如:
- 下订单或者买东西
- 知识问答,如Siri、谷歌助手、微软小冰等
完全理解和表达语言的内涵是极其困难的,完美的语言理解等效于实现完备的人工智能系统。

1.2 NLP的层次

语言的输入有两种方式,一种是语音识别,一种是文本(OCR和分词)。接下来是形态学(Morphology),简单可理解为对英文单词进行形态变换,如act->action。
接下来是语法分析和语义分析。最后是篇章处理,它更加注重于通过上下文进行理解。
本门课主要注重于画圈的三大部分,尤其是后两部分(语法分析和语义分析)。
1.3 自然语言处理应用


推荐和广告依然是AI在互联网行业落地最早也最为成熟的两个方向。所以将NLP技术利用于这两个方向也是顺其自然的事情。具体来说:
- 搜索(拼写自动纠正)
- 在线广告匹配
现如今NLP最火热的两个方向分别是知识图谱和智能客服(聊天机器人)。
1.4 人类语言的特殊之处

自然语言与信号处理、数据挖掘不同(后两者是处理数据,目的是从一堆随机数据中找出规律),自然语言都是用来传输有意义的信息的。另外,自然语言对应的系统很复杂,但是小孩子也能很快学会说话。人类语言是离散的、明确的符号系统。事实上,我们是用符号系统和别人交流,但这种富有表现力的系统可能会出现微小的差异,比如颜文字,随意的错误拼写“I loooove it”。有了符号以后,我们就可以进行可靠的远距离的传输。所以说语言文字并不仅仅是形式逻辑或传统AI的产物。

当人们使用语言进行交流,尽管交流的内容包括符号,但都是通过承载在连续的载体中的。一个有趣的现象是,使用不同的载体可以表达完全相同的信息。
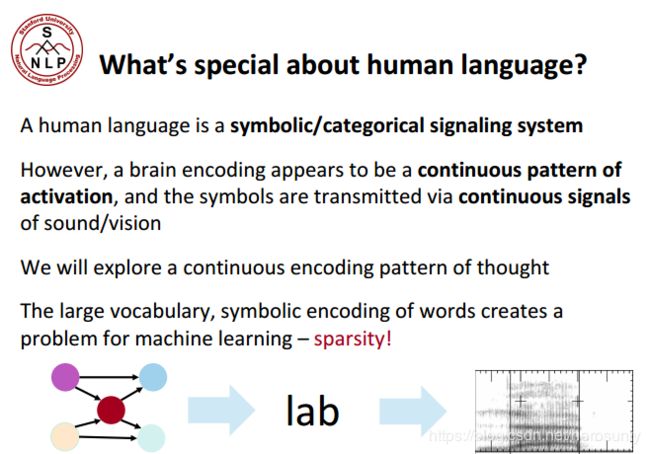 哲学、科学、人工智能的主要观点是把语言的符号体系映射到大脑。对于深度学习来说,可以把大脑想象成具有连续激活模式的大脑,上图表示的是,我们使用语言是把连续转换成符号,再转换成连续的过程。
哲学、科学、人工智能的主要观点是把语言的符号体系映射到大脑。对于深度学习来说,可以把大脑想象成具有连续激活模式的大脑,上图表示的是,我们使用语言是把连续转换成符号,再转换成连续的过程。
另外巨大的词表(每种语言最少有几万个词汇)也导致数据稀疏,是机器学习要解决的一个重要问题。
2. 如何表示词的含义

这部分内容不是很好理解,包括了人类的发展史、哲学思想等等,能发明符号表示含义看起来非常容易简单,但是从0到1绝对是智慧的表现。
2.1 如何在计算机中表示含义
pip install nltk
import nltk
nltk.download('wordnet')
相同词在不同词性下的同义词
from nltk.corpus import wordnet as wn
poses = { 'n':'noun', 'v':'verb', 's':'adj (s)', 'a':'adj', 'r':'adv'}
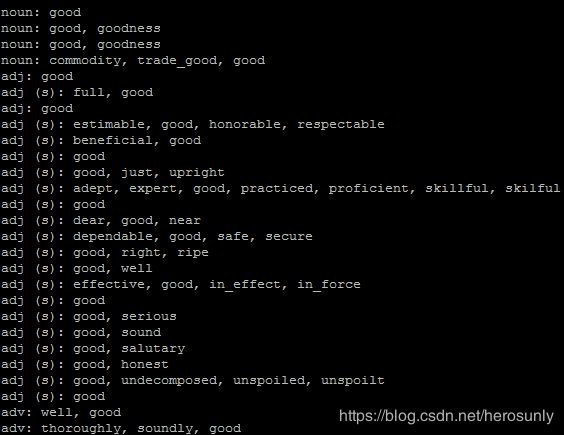
for synset in wn.synsets("good"):
print("{}: {}".format(poses[synset.pos()],
", ".join([l.name() for l in synset.lemmas()])))
from nltk.corpus import wordnet as wn
panda = wn.synset("panda.n.01")
hyper = lambda s: s.hypernyms()
list(panda.closure(hyper))
2.2 离散化表示


one-hot表示的问题在于,两个向量是正交的,所以无法计算向量之间的相似度。
2.3 分布式表示

通过相邻词来表示该词的含义(从小到大的阅读理解中都是使用该方法来判断新词的意思)。

使用分布式表示就可以用稠密的向量来代替系数的向量,并且可以表示词与词之间的相似性。

通过t-SNE将100维向量降维为2维的向量。
2.4 Word2Vec

大量的文本称为是语料。每个词由向量表示,并且由随机向量进行起始表示。
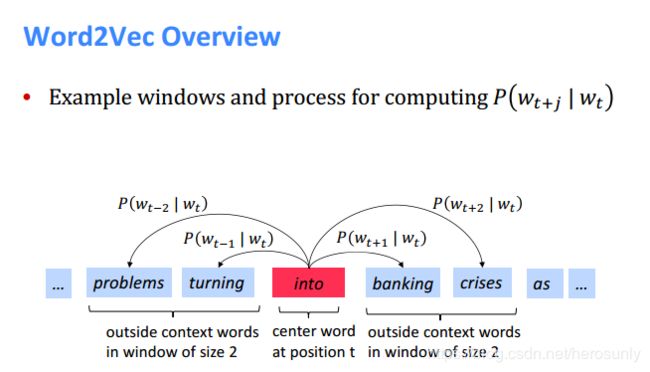
通过中心词计算背景词的概率
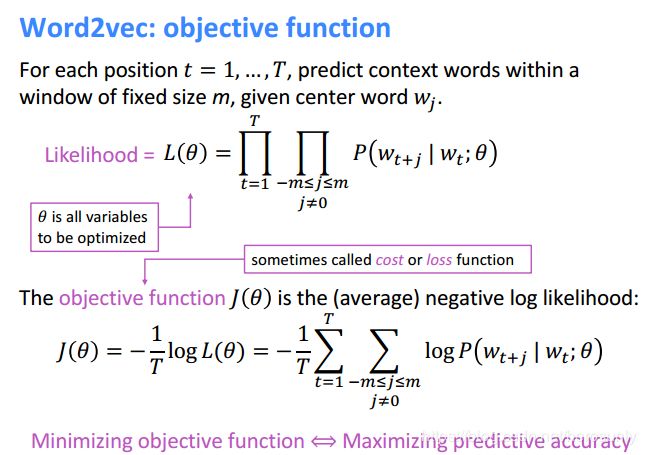
L ( θ ) = ∏ t = 1 T ∏ − m ≤ j ≤ m j j ≠ 0 P ( w t + j ∣ w t ; θ ) L(\theta)=\prod \limits_{t=1}^{T}\prod \limits_{-m\leq j \leq m _{j} \atop j \neq 0} P(w_{t+j}|w_t;\theta) L(θ)=t=1∏Tj=0−m≤j≤mj∏P(wt+j∣wt;θ)
J ( θ ) = − 1 T ∑ t = 1 T ∑ − m ≤ j ≤ m j ≠ 0 l o g P ( w t + j ∣ w t ; θ ) J(\theta)=-\frac{1}{T} \sum \limits _{t=1} ^{T} \sum \limits _{-m \leq j \leq m \atop {j \neq 0}} log P(w_{t+j}|w_t;\theta) J(θ)=−T1t=1∑Tj=0−m≤j≤m∑logP(wt+j∣wt;θ)

每个词都有两个对应的向量,即作为中心词 v w v_w vw和背景词的向量 u w u_w uw。基于中心词去预测背景词的概率如下所示:
P ( o ∣ c ) = P ( o , c ) P ( c ) = e x p ( u o T v c ) ∑ w ∈ v e x p ( u w T v c ) P(o|c)=\frac{P(o, c)}{P(c)}=\frac{exp(u_o^Tv_c)}{\sum_{w \in v} exp(u_w^Tv_c)} P(o∣c)=P(c)P(o,c)=∑w∈vexp(uwTvc)exp(uoTvc)

P ( o ∣ c ) P(o|c) P(o∣c)的表达式很类似于常用的softmax函数。其中max指的是会放大最大的 x i x_i xi,soft区别于hard,再小的 x i x_i xi也会有一定的概率(只是比较小)。

接下来我们对 P ( o ∣ c ) P(o|c) P(o∣c)求偏导。
J ( θ ) = − 1 T ∑ t = 1 T ∑ − m ≤ j ≤ m j ≠ 0 l o g P ( w t + j ∣ w t ) J(\theta)=-\frac{1}{T}\sum \limits _{t=1} ^T \sum \limits _{-m \leq j \leq m \atop j \neq 0}{log P(w_{t+j}|w_t)} J(θ)=−T1t=1∑Tj=0−m≤j≤m∑logP(wt+j∣wt)
P ( o ∣ c ) = e x p ( u o T v c ) ∑ w ∈ V e x p ( u w T v c ) P(o|c) = \frac{exp(u_o^Tv_c)}{\sum _{w \in V}exp(u_w^Tv_c)} P(o∣c)=∑w∈Vexp(uwTvc)exp(uoTvc)
∂ J ( θ ) ∂ v c = − 1 T ∑ t = 1 T ∑ − m ≤ j ≤ m j ≠ 0 l o g e x p ( u o T v c ) ∑ w ∈ V e x p ( u w T v c ) \frac{\partial{J(\theta)}}{\partial v_c}=-\frac{1}{T}\sum \limits _{t=1} ^T \sum \limits _{-m \leq j \leq m \atop j \neq 0} log \frac{exp(u_o^Tv_c)}{\sum _{w \in V}exp(u_w^Tv_c)} ∂vc∂J(θ)=−T1t=1∑Tj=0−m≤j≤m∑log∑w∈Vexp(uwTvc)exp(uoTvc)
为了简单起见,只计算求和部分的导数,先忽略求和符号。
由于后面会用到标量对向量的求导 ∂ u o T v c ∂ v c = u o \frac{\partial{u_o^Tv_c}}{\partial v_c}=u_o ∂vc∂uoTvc=uo,所以先说明一下。这个公式涉及到转置,有可能会让人有些疑惑,那该如何去思考这个问题呢?最简单的方法就是进行拆解,并且偏导的结果应该是和 v c v_c vc的形状一样(列向量):
u o T v c = u 1 ∗ v 1 + u 2 ∗ v 2 + … u_o^Tv_c=u_1*v_1+u_2*v_2+\dots uoTvc=u1∗v1+u2∗v2+… ∂ u o T v c ∂ v c = ( u 1 , u 2 , … ) T = u o \frac{\partial u_o^Tv_c}{\partial v_c}=(u_1,u_2,\dots)^T=u_o ∂vc∂uoTvc=(u1,u2,…)T=uo
∂ l o g ∑ w = 1 v e x p ( u w T v c ) ∂ v c = 1 ∑ w = 1 v e x p ( u w T v c ) ∑ x = 1 v e x p ( u x T v c ) ∗ u x = ∑ x = 1 v u x ∗ e x p ( u x T v c ) ∑ w = 1 v e x p ( u w T v c ) = \frac{\partial {log \sum \limits _{w=1} ^v} exp(u_w^T v_c)}{\partial{v_c}}=\frac{1}{\sum \limits _{w=1} ^v exp(u_w^Tv_c)} \sum \limits _{x=1} ^{v} exp(u_x^Tv_c) *u_x = \sum \limits _{x=1}^{v} \frac{u_x*exp(u_x^Tv_c)}{\sum \limits _{w=1} ^v exp(u_w^Tv_c)}= ∂vc∂logw=1∑vexp(uwTvc)=w=1∑vexp(uwTvc)1x=1∑vexp(uxTvc)∗ux=x=1∑vw=1∑vexp(uwTvc)ux∗exp(uxTvc)=
∂ l o g P ( o ∣ c ) ∂ v c = u o − ∑ w = 1 v u x ∗ P ( x ∣ c ) \frac{\partial logP(o|c)}{\partial v_c}=u_o-\sum \limits _{w=1} ^vu_x*P(x|c) ∂vc∂logP(o∣c)=uo−w=1∑vux∗P(x∣c)
后续代码地址为:http://web.stanford.edu/class/cs224n/materials/Gensim.zip,其中glove语言模型对应下载地址为https://nlp.stanford.edu/data/glove.6B.zip。
3. 代码
Gensim word vector visualization of various word vectors
import numpy as np
# Get the interactive Tools for Matplotlib
%matplotlib notebook
import matplotlib.pyplot as plt
plt.style.use('ggplot')
from sklearn.decomposition import PCA
from gensim.test.utils import datapath, get_tmpfile
from gensim.models import KeyedVectors
from gensim.scripts.glove2word2vec import glove2word2vec
glove_file = datapath('/home/ly/code/cs224n/glove.6B.100d.txt')
word2vec_glove_file = get_tmpfile("/home/ly/code/cs224n/glove.6B.100d.word2vec.txt")
glove2word2vec(glove_file, word2vec_glove_file)
model = KeyedVectors.load_word2vec_format(word2vec_glove_file)
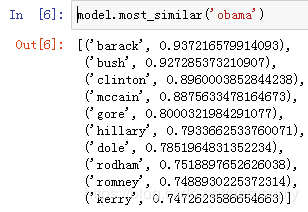
model.most_similar('obama')
model.most_similar('banana')
model.most_similar(negative='banana')
result = model.most_similar(positive=['woman', 'king'], negative=['man'])
print("{}: {:.4f}".format(*result[0]))
def analogy(x1, x2, y1):
result = model.most_similar(positive=[y1, x2], negative=[x1])
return result[0][0]
def display_pca_scatterplot(model, words=None, sample=0):
if words == None:
if sample > 0:
words = np.random.choice(list(model.vocab.keys()), sample)
else:
words = [ word for word in model.vocab ]
word_vectors = np.array([model[w] for w in words])
twodim = PCA().fit_transform(word_vectors)[:,:2]
plt.figure(figsize=(6,6))
plt.scatter(twodim[:,0], twodim[:,1], edgecolors='k', c='r')
for word, (x,y) in zip(words, twodim):
plt.text(x+0.05, y+0.05, word)
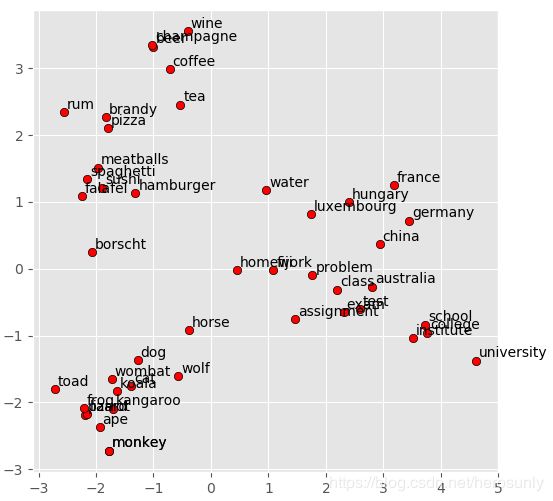
display_pca_scatterplot(model,
['coffee', 'tea', 'beer', 'wine', 'brandy', 'rum', 'champagne', 'water',
'spaghetti', 'borscht', 'hamburger', 'pizza', 'falafel', 'sushi', 'meatballs',
'dog', 'horse', 'cat', 'monkey', 'parrot', 'koala', 'lizard',
'frog', 'toad', 'monkey', 'ape', 'kangaroo', 'wombat', 'wolf',
'france', 'germany', 'hungary', 'luxembourg', 'australia', 'fiji', 'china',
'homework', 'assignment', 'problem', 'exam', 'test', 'class',
'school', 'college', 'university', 'institute'])
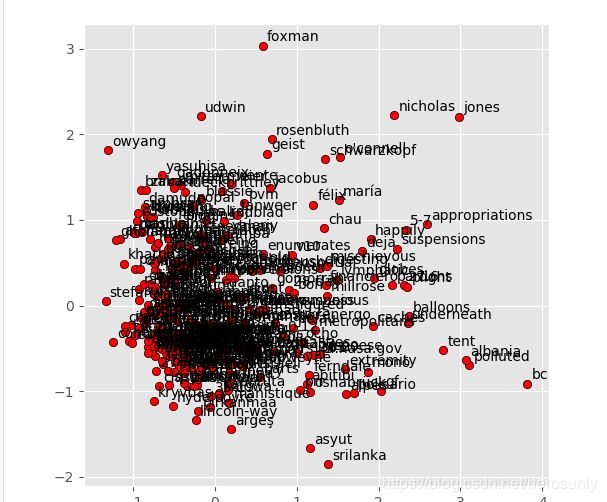
display_pca_scatterplot(model, sample=300)