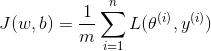Python与logistic回归——理解与实践

文章参考 https://www.cnblogs.com/chamie/p/4876149.html 【Machine Learning in Action --5】逻辑回归（LogisticRegression）从疝气病预测病马的死亡率

文章实例为疝气症预测病马死亡率，实例数据：http://archive.ics.uci.edu/ml/datasets/Horse+Colic

---

引言

logistic回归，一种广义的线性回归分析模型。常用于做二分类问题(非0即1)，但是logsitic回归并不是分类器，是一种概率估计，下文中会做详细解释。

---

问题提出 

给定  个个体 ，对每一组个体求预测值 ，使得  其中  为  维列向量， 中每一个元素都是个体特征，总共  个特征， 取值为0或1。

即是 ，。

对于文章的实例，就是给出300组数据(300个个体)，每组数据的  为病马的一些特征，例如年龄，呼吸频率等， 即是病马死亡(0)或病马存活(1)。

---

logistic函数

上述问题可用拟合的方法进行求解，由于是二分类问题，简单的线性回归  无法满足我们的需求(线性回归的值域为)，那么引出了sigmoid函数。

sigmoid函数 ，也称作logistic函数，特殊地 。

图像如图所示，简单可以看出sigmoid函数可以将线性回归  映射到  区间，问题并没有解决， 区间中仍有无限个点，不满足二分类，于是我们规定，这样logistic函数就满足了二分类问题。

值得注意的是，logistic回归并不是分类器，它只是一种概率估计，而是我们硬性的规定了分类标准(即大于0.5最终为1，小于0.5最终为0)，于是，对于分类器的某些结果测量评估，logistic回归的结果可能是不理想的。

---

logistic回归

现在有了回归函数 ，利用回归函数可以得到一组 ,希望 ，即是预测值尽可能的“贴近”精确值，此时定义损失函数(Loss function)，用于衡量单个个体的表现情况。

通常损失函数设计为均方误差，即 ，但是在logistic回归中，均方误差可能会产生非凸集(局部最优)，于是logistic回归损失函数为：

此损失函数利用最大似然估计得到，，可以看出来损失函数越小表现情况越优秀。

还需要定义一个衡量全体个体表现情况的参量，代价函数(Cost function)。

其中  为适当的缩放。可见  是一个凸函数，局部最小即是全体最小。我们的目的就是找到最佳拟合参数  使得  最小。

当然，也可以对  进行寻找极值求解  个方程得到最佳参数 ，然而对于实际问题求解方程是困难的，于是使用迭代法近似。

---

梯度下降法

常用的迭代法牛顿法、梯度下降法(最速下降法)、共轭迭代法、变尺度迭代法、最小二乘法。

梯度：对于可微的数量场 ，以  为分量的向量场称为  的梯度。

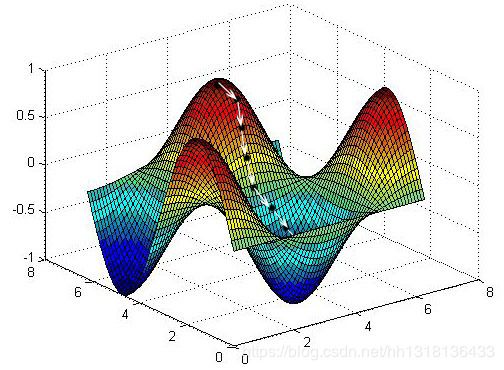
梯度是一个向量，表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大。总结一下即是，沿梯度正方向，函数上升最快；沿梯度反方向，函数下降最快。

如图所示，白线部分即为梯度下降过程。

必须注意的是，梯度下降法会遍历局部最低点，达到局部最优解，对于logistic回归， 函数不会出现局部最优，但考虑其他问题时，需谨慎。

假设特征数，由  ，  ，可以得到(推导公式省略)：

，，则梯度下降公式为：

，其中  为学习率(即步长)

---

算法概述

符号说明：

假设特征数 ，迭代次数 ，

设立初始值 ，

 //迭代次数

       

       

               //计算logistic函数

              

               //计算梯度，累加

              

       

       

         //梯度下降

       

---

算法实现

使用python语言，方便之处在于python丰富强大的第三方库。

“算法概述”模块的实例我假设特征数 ，但实际中特征数会远多于2(例如实例中的21个)，那么在算法实现中还需要一个for循环，那么整个算法3层for循环，如果使用python中的numpy库进行向量化运算，便可以减少运算时间。

例如，随机的1000维的行向量相加，for循环与numpy的时间比：

import numpy as np
import time
a = np.random.random((1000, 1))
b = np.random.random((1000, 1))
c = np.zeros((1000, 1))
start = time.perf_counter()
for i in range(a.shape[0]): #for-loop
    c[i] = a[i] + b[i]
end = time.perf_counter()
d = a + b #numpy
ennd = time.perf_counter()
print((end - start) * 1000, (ennd - end) * 1000)
'''
①2.272844999999996 0.00933100000000131
②2.300835000000001 0.008863999999997318
③2.272377999999992 0.008397000000021082
'''

可以清楚的看到，运行3次得到的结果都是numpy向量运算比for循环时间快了至少200倍。

这种巨大差异的原因，易于理解就是因为numpy是C语言写的，python是解释型语言，C是编译型语言，通常运算下C是比python快的。若探究巨大差异的本质的话，就是numpy可能会利用SIMD，超线程/多线程CPU，GPU进行向量化运算。(个人理解，有误请指出)

import numpy as np

'''
logistic函数
参数为ndarray的1维向量
'''
def sigmoid(x):
    return 1 / (1 + np.exp(-1 * x))

'''
logistic回归
参数为训练集(x,y),x为(m,n)维向量，y为(m,1)维向量
'''
def logisticRegression(x, y):
    alpha = 0.001 #alpha学习率
    cnt = 1000 #迭代次数
    n = x.shape[1] #特征个数
    w = np.ones(n)。reshape((n,1)) #初始化w向量,n阶列向量
    b = 0 #初始化b
    while cnt != 0:
        theta = sigmoid(np.dot(x, w) + b) #计算theta向量,m阶列向量
        dz = theta - y 
        dw = 1 / n * np.dot(x.T, dz) #计算梯度，n阶列向量
        db = 1 / n * np.sum(dz)
        w = w - alpha * dw.T #梯度下降，n阶列向量
        b = b - alpha * db
    return w, b

算法实现后的代码会有些难理解，因为我将“算法概述”中的两层for循环向量化了，不但代码长度减少，并且运算时间也减少了。例如：计算系数向量，其中 

dw = 1 / m * np.dot(x.T, dz) #与下方for循环代码作用一致
for i in range(m):
    for j in range(n):
        dw[i] = dw[i] + x[j][i] * dz[j]
    dw[i] = dw[i]/m

其余部分向量化代码就不做演示，自己理解。

---

实例练习

从开头的网址上下载horse-colic.data中有300个个体，作为训练集；horse-colic.test中有68个个体，作为测试集；horse-colic.names是对数据文档与个体特征的描述。

首先数据预处理，并不是所有的数据一拿到手就可以直接使用，需要人为的处理一下以便使用。观察文档，我们知道数据中有30%是缺失的，那么我们要丢掉这30%的数据吗？答案是不掉丢，因为有时数据相当昂贵，扔掉和重新获取都是不可取的，所以必须采用一些方法来解决这个问题。于是，对于缺失数据，我们有以下几种方法可选：

① 使用可用特征的均值来填补缺失值；

② 使用特征值来填补缺失值，如-1，0；

③ 忽略有缺失值的样本；(对于本实例此方法不可取，因为本实例数据量很小)

④ 使用相似样本的均值填补缺少值；

⑤ 使用另外的机器学习算法预测缺失值；

于此，我选择使用特征值0来填补缺失值，选择0的好处在于 ，这样一来缺失值对数据预测不具有任何倾向性，因此带来的误差可大大减少。这里的替换缺失值可以直接用txt的“替换”功能就可以了，简洁明了。

观察个体特征，总共有28个，但并不是28个都需要，第3项的医院编号并无预测价值，类似的还有24到28。第23项是马的最终结果(1=活着；2=死亡；3=安乐死)，也就是 ，算法处理二分类，于是将2与3都设置为0(我理解为安乐死是疝气症不严重但无法救治，死亡是疝气症严重到无法救治)。

以下是实例代码，logistic回归函数做少许修改，并且减少测试次数。

import numpy as np

'''
logistic函数
参数为ndarray的1维向量
'''
def sigmoid(x):
    return 1 / (1 + np.exp(-1 * x))

'''
数据预处理函数
参数为文件路径
'''
def dataPreprocess(dataLoad):
    file = open(dataLoad)
    data = []
    for line in file.readlines():
        tmp = list(map(float, line.strip().split()))
        tmp = tmp[:2] + tmp[3:23] #去掉某些列
        if tmp[-1] > 1: #将死亡特征变成0或1
            tmp[-1] = 0
        data.append(tmp)
    return np.array(data) #将数据处理为ndarray类型

'''
test测试函数
参数为特征参数w,位移量b,测试集testData
'''
def test(w, b, testData):
    error = 0
    for i in range(testData.shape[0]):
        tmp = testData[i][:-1].reshape((21, 1)) #取出特征
        ans = sigmoid(np.dot(w.T, tmp) + b)
        if ans > 0.5: #大于0.5规定为1
            ans = 1
        else: #小于0.5规定为0
            ans = 0
        if ans != testData[i][-1]: #预测失误
            error += 1
    errorRate = error / testData.shape[0]
    print("此次迭代的错误率为:" + str(errorRate))
    return errorRate

'''
logistic回归
参数为训练集(x,y),x(300,21),y(300,1)
'''
def logisticRegression(trainData, testData):
    x = trainData[:,:-1]
    y = trainData[:,-1].reshape((300, 1))
    alpha = 0.001 #alpha学习率
    cnt = 10 #迭代次数
    n = x.shape[1] #特征个数
    w = np.ones(n).reshape((n, 1)) #初始化w向量(21,1)
    b = 0 #初始化b
    sum = 0
    while cnt != 0:
        theta = sigmoid(np.dot(x, w) + b) #计算theta向量(300,1)
        dz = theta - y
        dw = 1 / n * np.dot(x.T, dz) #计算梯度(21,1)
        db = 1 / n * np.sum(dz)
        w = w - alpha * dw #梯度下降(21,1)
        b = b - alpha * db
        cnt = cnt - 1
        error = test(w, b, testData)
        sum += error
    print("10次迭代的平均错误率为:" + str(sum / 10))

if __name__ == '__main__':
    trainData = dataPreprocess('horse_data.txt')
    testData = dataPreprocess('horse_test.txt')
    logisticRegression(trainData, testData)

'''
此次迭代的错误率为:0.3088235294117647
此次迭代的错误率为:0.3088235294117647
此次迭代的错误率为:0.29411764705882354
此次迭代的错误率为:0.35294117647058826
此次迭代的错误率为:0.36764705882352944
此次迭代的错误率为:0.4264705882352941
此次迭代的错误率为:0.3235294117647059
此次迭代的错误率为:0.4852941176470588
此次迭代的错误率为:0.3088235294117647
此次迭代的错误率为:0.5
10次迭代的平均错误率为:0.36764705882352944
'''

由上述代码结果可知，平均预测错误率达到了0.3677，这个结果还是不错的，毕竟还有30%的数据缺失，且数据量太小。

---

结论

logistic回归是学习神经网络的基础之一，在此算法中还有许多可以改进的地方，比如我们可以用牛顿法进行迭代，收敛速度比较梯度下降打更快。

如果有发现我的错误，请指出，十分感谢！