一、决策树概述
1、决策树思想
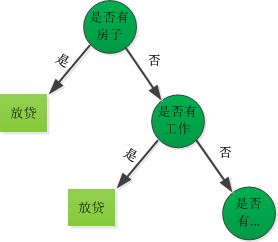
决策树思想的来源非常朴素,它来源于程序设计中的条件分支语句结构(if-then),最早的决策树就是利用这类结构分割数据的一种分类方法。例如,银行贷款是根据贷款人的各种条件来进行判断是否放贷:
可以看到银行贷款可以根据上面的条件依次进行判断,其中很重要的是为什么将是否有房子这个条件先进行判断呢?这也是决策树划分的核心,它的理论来源于信息论。
2、信息熵
信息论中很重要的一个概念就是信息熵,何为信息熵?在信息论中表述了信息的单位是比特,信息熵是衡量信息量的大小,假设现在有32支球队进行比赛,希望你来猜测一下那一支球队能取得胜利,那么最少的猜测次数应该是5。那么它的信息熵就是:
\[H = - ({P_1}\log {p_1} + {P_2}\log {p_2} + ... + {P_{32}}\log {p_{32}})\]
其中,P1...p2表示的是每一支球队获胜的概率(理论上来说都是1/32,所以对应的信息熵H=5)。H为信息熵,单位为比特。
公式为:
\[H(X) = \sum\nolimits_{X \in X} {{P_{(x)}}\log {p_{(x)}}} \]
3、信息增益
信息增益是决策树的划分依据之一,表示得知特征X的信息而使得类Y的信息的不确定性减少的程度,比如:上面银行贷款中将是否有房放在第一位,这样会让该后面的判断的不确定性减少的更多,从而判断出是否贷款。这种不确定减少的程度就是信息增益。
特征A对训练数据集D的信息增益g(D,A),定义为集合D的信息熵H(D)与特征A给定条件下D的信息条件熵H(D|A)之差,即公式为:
\[g(D,A) = H(D) - H(D|A)\]
假设下面是贷款的一些信息:
| ID |
是否有房子 |
是否有工作 |
信贷情况 |
类别 |
| 1 |
是 |
否 |
非常好 |
是 |
| 2 |
是 |
是 |
一般 |
是 |
| 3 |
否 |
是 |
好 |
否 |
| 4 |
否 |
是 |
好 |
否 |
| 5 |
否 |
否 |
一般 |
否 |
| 6 |
是 |
是 |
非常好 |
是 |
| 7 |
否 |
否 |
好 |
否 |
| 8 |
是 |
否 |
一般 |
否 |
| 9 |
否 |
否 |
一般 |
否 |
其中,是否有房子、是否有工作、信贷情况是其特征值;类别是其目标值,表示银行是否会放贷。我们可以利用信息增益的公式来进行计算,哪个特征应该最先放到首位。
上面的信息熵的计算:
\[H(D) = - \sum\limits_{k = 1}^k {\frac{{{C_k}}}{D}} \log \frac{{{C_k}}}{D}\]
其中,Ck表示属于某个类别的样本数。
条件熵的计算:
\[H(D|A) = \sum\limits_{i = 1}^n {\frac{{|{D_i}|}}{{|D|}}} H({D_i}) = - \sum\limits_{i = 1}^n {\frac{{|{D_i}|}}{{|D|}}} \sum\limits_{k = 1}^K {\frac{{|{D_{ik}}|}}{{|{D_i}|}}} \log \frac{{|{D_{ik}}|}}{{|{D_i}|}}\]
那么,我们可以利用上面的公式来计算一下:
- 总的信息熵H
H(D)=-3/9log3/9-6/9log6/9=0.36
- 每个特征的条件熵
#房子特征的信息增益 g(D,房子) = H(D)-H(D'|房子)=H(D)-[4/10H(是)+5/10H(否)] #求出房子中是的类别的熵,注意此处的熵都是针对于目标类别的(在房子是的情况与否的情况下) H(是)=-(3/4*log3/4+1/4*log1/4)=0.24 H(否)=-(5/5*log5/5+0/5*log0/5)=0 g(D,房子) = H(D)-H(D'|房子)=H(D)-[5/10H(是)+5/10H(否)]=H(D)=0.3 ...
上述算出的就是房子特征的信息增益,其余的与之计算方式一样,最后比较每个特征的信息的增益,这样就知道那个特征应该先进性判断。
4、常见的决策树算法
上面我们使用的是信息增益(ID3)的算法,进行决策树,当然还有其它的方法:
- 信息增益比(C4.5)
- 基尼系数(CART)
二、sklearn决策树API
1、class sklearn.tree.DecisionTreeClassifier(criterion=’gini’, max_depth=None,random_state=None)
上面就是决策树的分类器,其中:
- criterion:默认是’gini’系数(基尼系数),也可以选择信息增益的熵’entropy’
- max_depth:树的深度大小
- random_state:随机数种子
2、实例
现有泰坦尼克号乘客的数据集,现提取数据集中的特征是票的类别,存活,乘坐班,年龄,登陆,home.dest,房间,票,船和性别。乘坐班是指乘客班(1,2,3),是社会经济阶层的代表。数据集的部分内容如下:
注:其中age数据存在缺失。
"row.names","pclass","survived","name","age","embarked","home.dest","room","ticket","boat","sex" "1","1st",1,"Allen, Miss Elisabeth Walton",29.0000,"Southampton","St Louis, MO","B-5","24160 L221","2","female" "2","1st",0,"Allison, Miss Helen Loraine", 2.0000,"Southampton","Montreal, PQ / Chesterville, ON","C26","","","female" "3","1st",0,"Allison, Mr Hudson Joshua Creighton",30.0000,"Southampton","Montreal, PQ / Chesterville, ON","C26","","(135)","male" "4","1st",0,"Allison, Mrs Hudson J.C. (Bessie Waldo Daniels)",25.0000,"Southampton","Montreal, PQ / Chesterville, ON","C26","","","female" "5","1st",1,"Allison, Master Hudson Trevor", 0.9167,"Southampton","Montreal, PQ / Chesterville, ON","C22","","11","male" "6","1st",1,"Anderson, Mr Harry",47.0000,"Southampton","New York, NY","E-12","","3","male" ... ...
数据来源:http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt
对于上面的乘客生存的分类模型可按照下面的流程进行处理:
- 读取数据
- 选取特征、处理缺失值
- 进行特征工程(特征抽取)
- 执行决策树估计起流程
import pandas as pd from sklearn.model_selection import train_test_split from sklearn.feature_extraction import DictVectorizer from sklearn.tree import DecisionTreeClassifier, export_graphviz def decision(): """ 决策树对泰坦尼克号乘客进行生死预测 :return: None """ # 读取数据 data = pd.read_csv("./data/决策树数据/data.csv") # 选取特征值、目标值 x = data[['pclass', 'age', 'sex']] y = data['survived'] # 处理缺失值 x['age'].fillna(x['age'].mean(), inplace=True) print(x) """ pclass age sex 1st 29.000000 female 1st 2.000000 female ... """ # 分割数据集为训练集和测试集 x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25) # 特征工程,pclass与sex都是非数字的值,所以需要将其值得类别进行one-hot编码,使用字典抽取,age值不变 dict = DictVectorizer(sparse=False) x_train = dict.fit_transform(x_train.to_dict(orient='records')) x_test = dict.transform(x_test.to_dict(orient='records')) print(dict.get_feature_names()) # ['age', 'pclass=1st', 'pclass=2nd', 'pclass=3rd', 'sex=female', 'sex=male'] print(x_train) """ [[32. 0. 0. 1. 0. 1. ] ... [58. 1. 0. 0. 1. 0. ] [35. 0. 1. 0. 0. 1. ] [31.19418104 0. 0. 1. 0. 1. ]] """ # 用决策树进行预测 dtc = DecisionTreeClassifier() dtc.fit(x_train, y_train) # 预测准确率 print(dtc.score(x_test, y_test)) # 导出决策树结构 export_graphviz(dtc, out_file='./tree.dot',feature_names=['年龄', 'pclass=1st',
'pclass=2nd', 'pclass=3rd', '女性', '男性']) return None if __name__ == '__main__': decision()
三、优缺点
1、优点
- 树可被可视化,更易理解
- 数据不需要进行归一化这些操作,其它算法通常需要对其进行归一化处理(比如:k-近邻算法)
2、缺点
- 不能推广过于复杂的树,这被称之为过拟合,也就是说在训练集中过于追求完美分类,而在测试集中并没有很好的效果。
- 数据集中数据的一些小变化,可能会生成不同的决策树,这样导致决策树的不稳定。
对于以上缺点可采用下面的解决方案:
- 减枝cart算法
- 随机森林