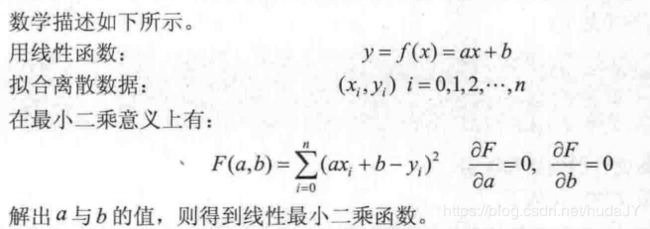matlab图形绘制之——最小二乘拟合
一、最小二乘法
记忆中是在高中阶段学习的最小二乘法。看一下最小二乘法的定义。
二、matlab中的polyfit
在Matlab中 使用polyfit()函数对数据进行最小二乘法拟合,调用格式:
p = polyfit(x,y,n) % 多项式曲线拟合
% 返回阶乘为n的多项式P(x)的系数.该阶乘是y中数据的最佳拟合(最小二乘法中)
% p 中的系数按降幂排列,p 的长度为 n+1 (p:向量)
例如:x,y是给定的数据中的所有点的横坐标和纵坐标,n为要拟合的线性的幂。
p = polyfit(x,y,2); % 这里polyfit 即表示用一个最高次为 2次的多项式来拟合
返回的p:计算出来的拟合曲线对应的幂的系数。 按照降幂排列。
如:得到的 p 为:3 2 3 即对应的拟合曲线为:3*x^2 + 2*x + 3;
三、实例
给定x,y的数据集
x = [0.5,1.0,1.5,2.0,2.5,3.0];
y = [1.75,2.45,3.81,4.80,7.00,8.60];
分别用1次 2次 3次 进行拟合 绘制出相应曲线
代码:
clc,clear,close all;
x = [0.5,1.0,1.5,2.0,2.5,3.0];
y = [1.75,2.45,3.81,4.80,7.00,8.60];
a1 = polyfit(x,y,1); % n=1 的 一次拟合
a2 = polyfit(x,y,2); % 二次拟合
a3 = polyfit(x,y,3); % 三次拟合
% a: 返回的是拟合曲线的系数的降幂排列
x1 = [0.5:0.05:3.0]; % 拟合曲线的 x 的取值
y1 = a1(1)*x1 + a1(2); % 一次多项式
y2 = a2(1).*x1.*x1 + a2(2)*x1 + a2(3); %二次多项式
y3 = a3(1).*x1.*x1.*x1 + a3(2).*x1.*x1 + a3(3)*x1 + a3(4); %三次多项式
% 根据返回的系数 a 得到拟合曲线 y1 y2 y3
plot(x,y,'*');
hold on;
plot(x1,y1,'b--',x1,y2,'k',x1,y3,'ro-');
legend('原始数据','一次拟合','二次拟合','三次拟合');补充说明:
x 是给定的原始数据的横坐标点。
x1 是拟合曲线要使用的横坐标的值(因为要绘制曲线图),是较为精细的。
根据a0 a1 a2 得到三条拟合曲线为: y1, y2, y3
以x1 作为横坐标,绘制出拟合曲线y1, y2, y3: plot(x1,y1,'b--',x1,y2,'k',x1,y3,'ro-');
legend(label1,...,labelN)
// 为每个绘制的数据序列创建一个带有描述性标签的图例.
// plot(x1,y1,'b--',x1,y2,'k',x1,y3,'ro-');
// legend('原始数据','一次拟合','二次拟合','三次拟合');
得到的图形界面:
说明: 以上例题来自《MATLAB经典案例实战》一书。
部分知识点来自 matlab官方文档