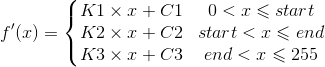C++数字图像处理(2)—分段线性拉伸
1、算法原理
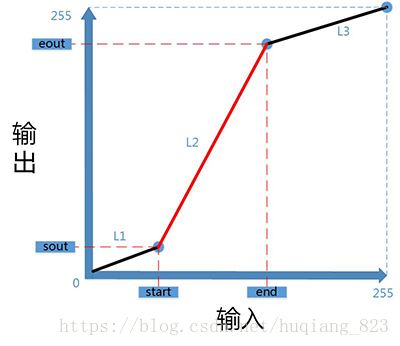
分段线性拉伸算法是图像灰度变换中常用的算法,在商业图像编辑软件Photoshop中也有相应的功能。分段线性拉伸主要是用于提高图像对比度,突显图像细节。设输入图像为f(x),输出图像为f'(x),分段区间为[start end]映射区间为[sout eout]。分段线性拉伸示意图如下:
图(1)分段线性拉伸示意图
从图(1)可以明显得到,分段线性拉伸算法需要明确4个参数start、end、sout以及eout。当这个四个参数均已知时,根据两点确定直线法,计算出直线L1、L2和L3的参数,分别为(K1、C1=0)、(K2、C2)和(K2、C2)。那么分段线性拉伸算法的公式如下:
对于参数分段区间[start end]以及映射区间[sout eout],有人工设定、基于直方图设定等办法。下面我们先实现核心算法功能,再实现参数半自动选取功能(基于直方图的分段线性拉伸)。
2、算法实现
由于分段线性拉伸也是图像灰度变换的一种,所以,在这篇文章中同样使用查表的方式进行算法实现。灰度变换查表法实现
//函数名:dividedLinearStrength
//作用:实现分段线性拉伸
//参数:
//matInput:输入图像
//matOutput : 输出图像
//fStart : 分段区间起点
//fEnd : 分段区间终点
//fSout:映射区间起点
//fEout:映射区间终点
//返回值:无
//注:支持单通道8位灰度图像
void dividedLinearStrength(cv::Mat& matInput, cv::Mat& matOutput, float fStart, float fEnd,
float fSout, float fEout)
{
//计算直线参数
//L1
float fK1 = fSout / fStart;
//L2
float fK2 = (fEout - fSout) / (fEnd - fStart);
float fC2 = fSout - fK2 * fStart;
//L3
float fK3 = (255.0f - fEout) / (255.0f - fEnd);
float fC3 = 255.0f - fK3 * 255.0f;
//建立查询表
std::vector loolUpTable(256);
for (size_t m = 0; m < 256; m++)
{
if (m < fStart)
{
loolUpTable[m] = static_cast(m * fK1);
}
else if (m > fEnd)
{
loolUpTable[m] = static_cast(m * fK3 + fC3);
}
else
{
loolUpTable[m] = static_cast(m * fK2 + fC2);
}
}
//构造输出图像
matOutput = cv::Mat::zeros(matInput.rows, matInput.cols, matInput.type());
//灰度映射
for (size_t r = 0; r < matInput.rows; r++)
{
unsigned char* pInput = matInput.data + r * matInput.step[0];
unsigned char* pOutput = matOutput.data + r * matOutput.step[0];
for (size_t c = 0; c < matInput.cols; c++)
{
//查表gamma变换
pOutput[c] = loolUpTable[pInput[c]];
}
}
} 参数设置fstart = 72、fEnd = 200、fSout=5、fEout=240,调用函数如下:
int _tmain(int argc, _TCHAR* argv[])
{
cv::Mat matSrc = cv::imread("../分段线性拉伸.jpg", cv::IMREAD_GRAYSCALE);
cv::imshow("原始图", matSrc);
cv::Mat matDLS;
dividedLinearStrength(matSrc, matDLS, 72, 200, 5, 240);
cv::imshow("分段线性拉伸", matDLS);
cv::waitKey(0);
return 0;
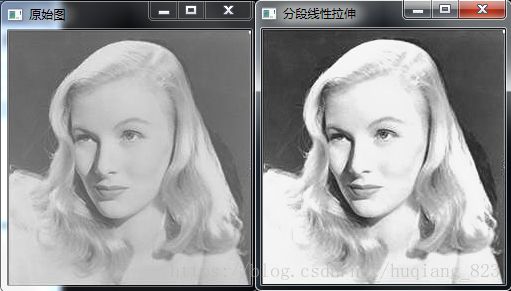
}运行效果如下:
图(2)分段线性拉伸
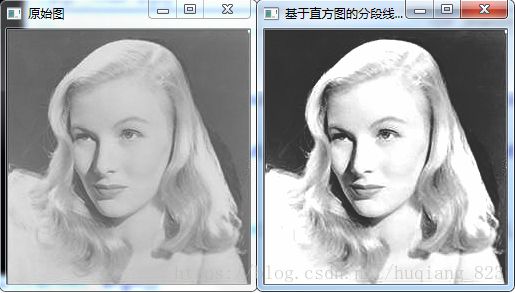
3、基于直方图的分段线性拉伸
基于直方图的分段线性拉伸算法主要改进在于,通过从直方图自动地计算出分段区间和映射区间四个参数。本质上,直方图是对图像像素进行排序的一个过程。根据分段线性拉伸的原理,对图像像素进行升序排序后,取高灰度等级NH个点对应的最小灰度作为fEnd,取低灰度等级NL个点对应的最大灰度等级作为fStart,fSout = fStart * Sigma, fEout = fEnd * (1+sigma),sigma < 1。具体代码实现步骤为:
(1)、统计直方图。
(2)、计算分段区间和映射区间。为使参数与图像尺寸无关,使用比例的方法限定NH和NL。设图像尺寸为MXN,高灰度等级个数比例为fH、低灰度等级个数比例为fL。
(3)、分段线性拉伸。
具体代码实现如下:
//函数名:dlsBaseHistogram
//作用:基于直方图的分段线性拉伸
//参数:
//matInput:输入图像
//matOutput : 输出图像
//fH : 高灰度等级比例
//fL : 低灰度等级比例
//fSigma:拉伸系数
//返回值:无
//注:支持单通道8位灰度图像
void dlsBaseHistogram(cv::Mat& matInput, cv::Mat& matOutput, float fH, float fL, float fSigma)
{
//统计直方图
std::vector histogram(256);
for (size_t r = 0; r < matInput.rows; r++)
for (size_t c = 0; c < matInput.cols; c++)
{
histogram[matInput.at(r, c)]++;
}
//计算分段区间
int nNH = matInput.rows * matInput.cols * fH;
int nNL = matInput.rows * matInput.cols * fL;
int nACC = 0;
float fStart = 0, fEnd = 0;
for (size_t m = 255; m >= 0; m --)
{
nACC += histogram[m];
if (nACC > nNH)
{
fEnd = m;
break;
}
}
nACC = 0;
for (size_t m = 0; m < histogram.size(); m++)
{
nACC += histogram[m];
if (nACC > nNL)
{
fStart = m;
break;
}
}
//计算映射区间
float fSout = fStart * fSigma;
float fEout = fEnd * (fSigma + 1.0f);
fEout = fEout > 255.0f ? 254 : fEout;
//分段线性拉伸
dividedLinearStrength(matInput, matOutput, fStart, fEnd, fSout, fEout);
}