机器学习算法与Python实践之(六)二分k均值聚类
机器学习算法与Python实践之(六)二分k均值聚类
http://blog.csdn.net/zouxy09
机器学习算法与Python实践这个系列主要是参考《机器学习实战》这本书。因为自己想学习Python,然后也想对一些机器学习算法加深下了解,所以就想通过Python来实现几个比较常用的机器学习算法。恰好遇见这本同样定位的书籍,所以就参考这本书的过程来学习了。
在上一个博文中,我们聊到了k-means算法。但k-means算法有个比较大的缺点就是对初始k个质心点的选取比较敏感。有人提出了一个二分k均值(bisecting k-means)算法,它的出现就是为了一定情况下解决这个问题的。也就是说它对初始的k个质心的选择不太敏感。那下面我们就来了解和实现下这个算法。
一、二分k均值(bisecting k-means)算法
二分k均值(bisecting k-means)算法的主要思想是:首先将所有点作为一个簇,然后将该簇一分为二。之后选择能最大程度降低聚类代价函数(也就是误差平方和)的簇划分为两个簇。以此进行下去,直到簇的数目等于用户给定的数目k为止。
以上隐含着一个原则是:因为聚类的误差平方和能够衡量聚类性能,该值越小表示数据点月接近于它们的质心,聚类效果就越好。所以我们就需要对误差平方和最大的簇进行再一次的划分,因为误差平方和越大,表示该簇聚类越不好,越有可能是多个簇被当成一个簇了,所以我们首先需要对这个簇进行划分。
二分k均值算法的伪代码如下:
***************************************************************
将所有数据点看成一个簇
当簇数目小于k时
对每一个簇
计算总误差
在给定的簇上面进行k-均值聚类(k=2)
计算将该簇一分为二后的总误差
选择使得误差最小的那个簇进行划分操作
***************************************************************
二、Python实现
我使用的Python是2.7.5版本的。附加的库有Numpy和Matplotlib。具体的安装和配置见前面的博文。在代码中已经有了比较详细的注释了。不知道有没有错误的地方,如果有,还望大家指正(每次的运行结果都有可能不同)。里面我写了个可视化结果的函数,但只能在二维的数据上面使用。直接贴代码:
biKmeans.py
#################################################
# kmeans: k-means cluster
# Author : zouxy
# Date : 2013-12-25
# HomePage : http://blog.csdn.net/zouxy09
# Email : [email protected]
#################################################
from numpy import *
import time
import matplotlib.pyplot as plt
# calculate Euclidean distance
def euclDistance(vector1, vector2):
return sqrt(sum(power(vector2 - vector1, 2)))
# init centroids with random samples
def initCentroids(dataSet, k):
numSamples, dim = dataSet.shape
centroids = zeros((k, dim))
for i in range(k):
index = int(random.uniform(0, numSamples))
centroids[i, :] = dataSet[index, :]
return centroids
# k-means cluster
def kmeans(dataSet, k):
numSamples = dataSet.shape[0]
# first column stores which cluster this sample belongs to,
# second column stores the error between this sample and its centroid
clusterAssment = mat(zeros((numSamples, 2)))
clusterChanged = True
## step 1: init centroids
centroids = initCentroids(dataSet, k)
while clusterChanged:
clusterChanged = False
## for each sample
for i in xrange(numSamples):
minDist = 100000.0
minIndex = 0
## for each centroid
## step 2: find the centroid who is closest
for j in range(k):
distance = euclDistance(centroids[j, :], dataSet[i, :])
if distance < minDist:
minDist = distance
minIndex = j
## step 3: update its cluster
if clusterAssment[i, 0] != minIndex:
clusterChanged = True
clusterAssment[i, :] = minIndex, minDist**2
## step 4: update centroids
for j in range(k):
pointsInCluster = dataSet[nonzero(clusterAssment[:, 0].A == j)[0]]
centroids[j, :] = mean(pointsInCluster, axis = 0)
print 'Congratulations, cluster using k-means complete!'
return centroids, clusterAssment
# bisecting k-means cluster
def biKmeans(dataSet, k):
numSamples = dataSet.shape[0]
# first column stores which cluster this sample belongs to,
# second column stores the error between this sample and its centroid
clusterAssment = mat(zeros((numSamples, 2)))
# step 1: the init cluster is the whole data set
centroid = mean(dataSet, axis = 0).tolist()[0]
centList = [centroid]
for i in xrange(numSamples):
clusterAssment[i, 1] = euclDistance(mat(centroid), dataSet[i, :])**2
while len(centList) < k:
# min sum of square error
minSSE = 100000.0
numCurrCluster = len(centList)
# for each cluster
for i in range(numCurrCluster):
# step 2: get samples in cluster i
pointsInCurrCluster = dataSet[nonzero(clusterAssment[:, 0].A == i)[0], :]
# step 3: cluster it to 2 sub-clusters using k-means
centroids, splitClusterAssment = kmeans(pointsInCurrCluster, 2)
# step 4: calculate the sum of square error after split this cluster
splitSSE = sum(splitClusterAssment[:, 1])
notSplitSSE = sum(clusterAssment[nonzero(clusterAssment[:, 0].A != i)[0], 1])
currSplitSSE = splitSSE + notSplitSSE
# step 5: find the best split cluster which has the min sum of square error
if currSplitSSE < minSSE:
minSSE = currSplitSSE
bestCentroidToSplit = i
bestNewCentroids = centroids.copy()
bestClusterAssment = splitClusterAssment.copy()
# step 6: modify the cluster index for adding new cluster
bestClusterAssment[nonzero(bestClusterAssment[:, 0].A == 1)[0], 0] = numCurrCluster
bestClusterAssment[nonzero(bestClusterAssment[:, 0].A == 0)[0], 0] = bestCentroidToSplit
# step 7: update and append the centroids of the new 2 sub-cluster
centList[bestCentroidToSplit] = bestNewCentroids[0, :]
centList.append(bestNewCentroids[1, :])
# step 8: update the index and error of the samples whose cluster have been changed
clusterAssment[nonzero(clusterAssment[:, 0].A == bestCentroidToSplit), :] = bestClusterAssment
print 'Congratulations, cluster using bi-kmeans complete!'
return mat(centList), clusterAssment
# show your cluster only available with 2-D data
def showCluster(dataSet, k, centroids, clusterAssment):
numSamples, dim = dataSet.shape
if dim != 2:
print "Sorry! I can not draw because the dimension of your data is not 2!"
return 1
mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', ' len(mark):
print "Sorry! Your k is too large! please contact Zouxy"
return 1
# draw all samples
for i in xrange(numSamples):
markIndex = int(clusterAssment[i, 0])
plt.plot(dataSet[i, 0], dataSet[i, 1], mark[markIndex])
mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', ' 三、测试结果
测试数据是二维的,共80个样本。有4个类。具体见上一个博文。
测试代码:
test_biKmeans.py
#################################################
# kmeans: k-means cluster
# Author : zouxy
# Date : 2013-12-25
# HomePage : http://blog.csdn.net/zouxy09
# Email : [email protected]
#################################################
from numpy import *
import time
import matplotlib.pyplot as plt
## step 1: load data
print "step 1: load data..."
dataSet = []
fileIn = open('E:/Python/Machine Learning in Action/testSet.txt')
for line in fileIn.readlines():
lineArr = line.strip().split('\t')
dataSet.append([float(lineArr[0]), float(lineArr[1])])
## step 2: clustering...
print "step 2: clustering..."
dataSet = mat(dataSet)
k = 4
centroids, clusterAssment = biKmeans(dataSet, k)
## step 3: show the result
print "step 3: show the result..."
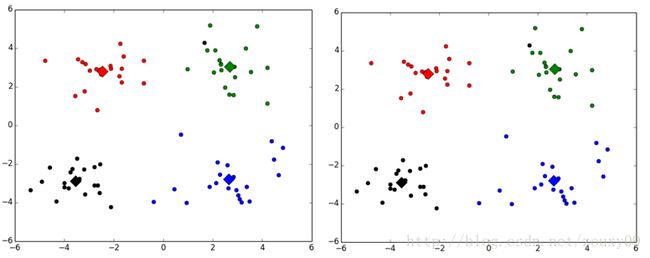
showCluster(dataSet, k, centroids, clusterAssment)这里贴出两次的运行结果:
不同的类用不同的颜色来表示,其中的大菱形是对应类的均值质心点。
事实上,这个算法在初始质心选择不同时运行效果也会不同。我没有看初始的论文,不确定它究竟是不是一定会收敛到全局最小值。《机器学习实战》这本书说是可以的,但因为每次运行的结果不同,所以我有点怀疑,自己去找资料也没找到相关的说明。对这个算法有了解的还望您不吝指点下,谢谢。