卷积神经网络学习笔记
Deep Learning是全部深度学习算法的总称,CNN是深度学习算法在图像处理领域的一个应用。
卷积神经网络简介(Convolutional Neural Networks,简称CNN)
1. 首先介绍卷积神经网络相关的几个名词。
在图像处理中,往往把图像表示为像素的向量,比如一个1000×1000的图像,可以表示为一个1000000的向量。在上一节中提到的神经网络中,如果隐含层数目与输入层一样,即也是1000000时,那么输入层到隐含层的参数数据为1000000×1000000=10^12,这样就太多了,基本没法训练。所以必须减少参数以加快速度。卷积神经网络有两种神器可以降低参数数目,一个是局部感知野,另一个是权值共享(参数共享)。
(1)局部感知野——每个神经元只需对局部进行感知,然后在更高层将局部的信息综合起来。
一般认为人对外界的认知是从局部到全局的,而图像的空间联系也是局部的像素联系较为紧密,而距离较远的像素相关性则较弱。因而,每个神经元其实没有必要对全局图像进行感知,只需要对局部进行感知,然后在更高层将局部的信息综合起来就得到了全局的信息。如下图所示:左图为全连接,右图为局部连接。
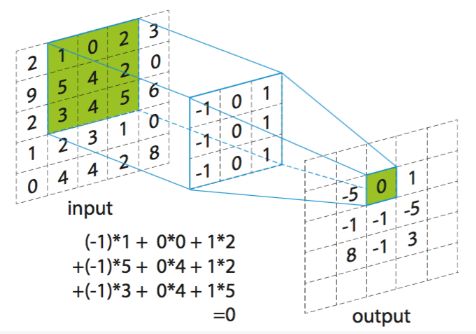
在上右图中,假如每个神经元只和10×10个像素值相连,那么权值数据为1000000×100个参数,减少为原来的千分之一。而那10×10个像素值对应的10×10个参数,其实就相当于卷积操作。
(2)权值共享—— 在一个部分学习的特征也能用在另一部分上。
从一个大尺寸图像中随机选取一小块,比如 8 ×8 , 学习到特征,可以用该特征跟原图作卷积。
在上面的局部连接中,每个神经元都对应100个参数,一共1000000个神经元,如果这1000000个神经元的100个参数都是相等的,那么参数数目就变为100了。这其中隐含的原理则是:图像的一部分的统计特性与其他部分是一样的。这也意味着我们在这一部分学习的特征也能用在另一部分上,所以对于这个图像上的所有位置,我们都能使用同样的学习特征。
更直观一些,当从一个大尺寸图像中随机选取一小块,比如说 8×8 作为样本,并且从这个小块样本中学习到了一些特征,这时我们可以把从这个 8×8 样本中学习到的特征作为探测器,应用到这个图像的任意地方中去。特别是,我们可以用从 8×8 样本中所学习到的特征跟原本的大尺寸图像作卷积,从而对这个大尺寸图像上的任一位置获得一个不同特征的激活值。
(3)多卷积核—— n个卷积核,可以学习n种特征,生成n幅图像。
上面所述只有100个参数时,表明只有1个100*100的卷积核,显然,特征提取是不充分的,我们可以添加多个卷积核,比如32个卷积核,可以学习32种特征。每个卷积核都会将图像生成为另一幅图像。
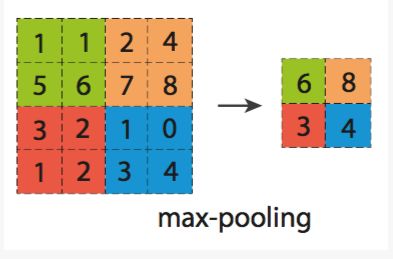
(4)池化(下采样)—— 对不同位置的特征进行聚合统计(平均值、最大值),降低特征维度,不易过拟合。
例如,人们可以计算图像一个区域上的某个特定特征的平均值 (或最大值)。这些概要统计特征不仅具有低得多的维度 (相比使用所有提取得到的特征),同时还会改善结果(不容易过拟合)。
2. 卷积神经网络的基本结构。
(1)特征提取层:每个神经元的输入与前一层的局部感受野相连,并提取该局部的特征。
(2)特征映射层:求局部平均、二次提取
或者,
(1)卷积层:采用各种卷积核对输入图片进行卷积处理。(平移不变性)
(2)池化层:降采样。(空间不变性)
全连接层:一个神经元作用于整个slice,即filter的尺寸恰好为一个slice的尺寸。
一般地,CNN的基本结构包括两层,其一为特征提取层,每个神经元的输入与前一层的局部接受域相连,并提取该局部的特征。一旦该局部特征被提取后,它与其它特征间的位置关系也随之确定下来;其二是特征映射层,网络的每个计算层由多个特征映射组成,每个特征映射是一个平面,平面上所有神经元的权值相等。特征映射结构采用影响函数核小的sigmoid函数作为卷积网络的激活函数,使得特征映射具有位移不变性。此外,由于一个映射面上的神经元共享权值,因而减少了网络自由参数的个数。卷积神经网络中的每一个卷积层都紧跟着一个用来求局部平均与二次提取的计算层,这种特有的两次特征提取结构减小了特征分辨率。
上图展示的是一个典型的卷积神经网络结构。这个网络包含两个卷积层(convolutionlayer),两个池化层(pooling layer)和一个全连接层(fully connected layer)。
3.
激励函数:根据一系列的输入值,神经元之间连接的权值以及激励规则,刺激神经元。
损失函数:在训练阶段,用于评估网络输出结果与实际值的差异。然后用损失函数的值更新每个神经元之间的权重值。卷积神经网络的训练目的就是最小化损失函数值。
4.
(1)假设输入图像尺寸为W,卷积核尺寸为F,步幅(stride)为S(卷积核移动的步幅),Padding使用P(用于填充输入图像的边界,一般填充0),那么经过该卷积层后输出的图像尺寸为(W-F+2P)/S+1。
(2)池化层通过减小中间过程产生的特征图的尺寸(下采样,图像深度不变),从而减小参数规模,降低计算复杂度,也可以防止过拟合。池化是分别独立作用于图像深度方向上的每个slice,一般使用Max操作(在一个局部区域内取最大值代表该区域),即最大池。通常池化层的空间尺寸(spatial extent)不应过大,过大会丢失太多结构信息,一般取F=3,S=2或者F=2,S=2。也有人不建议使用池化,而是在卷积层增大stride来降低图像尺寸。
(3)全连接层中一个神经元作用于整个slice,即filter的尺寸恰好为一个slice的尺寸,这样输出一个值,如果有n个filter,则输出长度为n的向量,一般全连接层的输出为类别/分数向量(class scores )。
5.注意:
(1)尽量使用多层fliter尺寸小的卷积层代替一层filter较大的卷积层。
(2)一般stride设为1,实际表现效果更好,将下采样的工作全部交给池化层。
(3)一般padding的大小为P=(F-1)/2,其中F为filter的尺寸。好处是使得卷积前后的图像尺寸保持相同,可以保持边界的信息。
(4)输入层(input layer)尺寸一般应该能被2整除很多次,比如32(CIFAR-10),64,96(STL-10),224(commonImageNet ConvNets),384和512。
(5)有时候由于参数太多,内存限制,会在第一个卷积层使用较大filter(7x7)和stride(2)(参考 ZF Net),或者filter(11x11),stride(4)。
6.卷积神经网络的优点
(1)主要用来识别位移、缩放及其他形式扭曲不变性的二维图形;
(2)避免了显示的特征抽取,而隐式地从训练数据中进行学习;
(3)由于同一特征映射面上的神经元权值相同,所以网络可以并行学习;
(4)权值共享降低了网络的复杂性;
(5)以其局部权值共享的特殊结构在语音识别和图像处理方面有着独特的优越性。
7.总结:
(1)CNN和其他机器学习算法一样,可以当成是一个分类器,像黑盒子一样使用它。
(2)Deep Learning强大的地方就是可以利用网络中间某一层的输出当作是数据的另一种表达,从而可以将其认为是经过网络学习到的特征。基于该特征,可以进行进一步的相似度比较等。
(3)Deep Learning算法能够有效的关键其实是大规模的数据,这一点原因在于每个DL都有众多的参数,少量数据无法将参数训练充分。