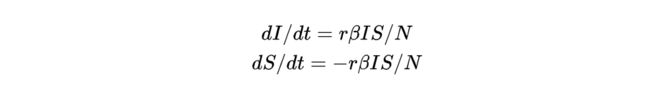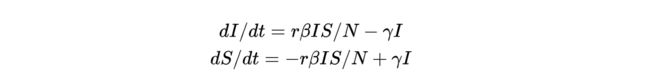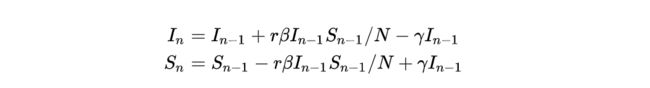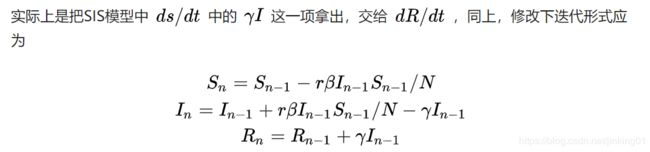在家宅着也能抵抗肺炎!玩一玩SEIR传染病模型
这几天的武汉肺炎疫情沸沸扬扬,为了抗击新型肺炎,整天宅在家里。七八年前刚入门社交网络相关研究的时候,接触了一下经典的传染病模型,如SI,SIS,SIR等。目前,朋友圈到处在传这波疫情的后续发展的趋势预测,于是准备再把这些东西捡起来,看看到底是个啥情况。
SI模型
我们先从最简单的SI模型学起,首先我们把人群分为2种,一种是易感者(Susceptibles),易感者是健康的人群,用 S 表示其人数,另外一种是感染者(The Infected),即患者,人数用 I 来表示。我们假设一个区域内总人数是N,即 N=S+I ,
有 I 个感染者整天到处溜达,每天碰到 r个人,有 b 的概率会传染疾病,健康人比例为 S/N 将以上所有量乘在一起就是每天新增感染病例,我们看下其微分方程形式
有了这么一个公式我们就可以进行仿真了,上述式子实际上就是一个马尔科夫链
马尔可夫链(Markov chain),又称离散时间马尔可夫链(discrete-time Markov chain),因俄国数学家安德烈·马尔可夫(俄语:Андрей Андреевич Марков)得名,为状态空间中经过从一个状态到另一个状态的转换的随机过程。该过程要求具备“无记忆”的性质:下一状态的概率分布只能由当前状态决定,在时间序列中它前面的事件均与之无关。
用在这里也一样,即当天的感染情况只和前一天的疾病感染人数有关。第N天的的人数我们可以表示为
来,上matab仿真,看看效果
%--------------------------------------------------------------------------
% 初始化
%--------------------------------------------------------------------------
clear;clc;
%--------------------------------------------------------------------------
% 参数设置
%--------------------------------------------------------------------------
N = 10000; %人口总数
I = 1; %传染者
S = N - I; %易感者
r = 10; %感染者接触易感者的人数
B = 0.01; %传染概率
T = 1:200;
for idx = 1:length(T)-1
S(idx+1) = S(idx) - r*B*I(idx)*S(idx)/N;
I(idx+1) = I(idx) + r*B*I(idx)*S(idx)/N;
end
plot(T,S,T,I);grid on;
xlabel('天');ylabel('人数')
legend('易感者','传染者');title('SI模型')我们设置的初始条件为人数 N=10000,初始感染者 I=1 ,每天闲逛到处溜达接触的人数是 r=10 ,接触后传染的概率为 b=0.01 。
也就是说,要是没人管让传染者整天在街上红哒哒白哒哒,那完蛋了,全部都得中招!
这个模型还是比较简单,一旦中招无法治愈,整个一生化危机。
SIS模型
我们加点料,增加点复杂度,有的人治好了但是还会反复感染,类似流感这样子。
这样子的模型就是SIS模型,SIS模型比SI模型多了一个感染者 I 恢复健康的概率 ![]() 。
。
再次加入到迭代方程里面
那么,同马尔科夫链一样,修改下公式应该为
略微修改下SI的代码我们就得到了SIS模型
%--------------------------------------------------------------------------
% 初始化
%--------------------------------------------------------------------------
clear;clc;
%--------------------------------------------------------------------------
% 参数设置
%--------------------------------------------------------------------------
N = 10000; %人口总数
I = 1; %传染者
S = N - I; %易感者
r = 10; %感染者接触易感者的人数
B = 0.01; %传染概率
y = 0.02; %康复概率
T = 1:200;
for idx = 1:length(T)-1
S(idx+1) = S(idx) - r*B*I(idx)*S(idx)/N + y*I(idx);
I(idx+1) = I(idx) + r*B*I(idx)*S(idx)/N - y*I(idx);
end
plot(T,S,T,I);grid on;
xlabel('天');ylabel('人数')
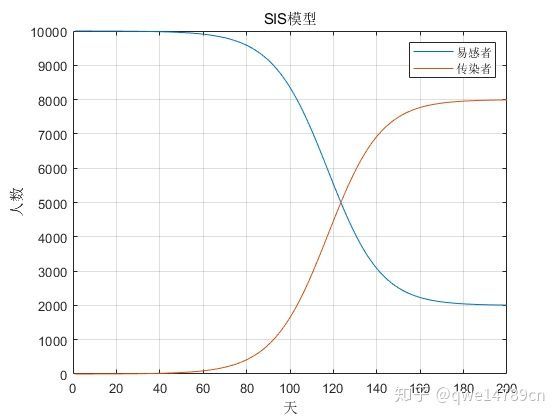
legend('易感者','传染者');title('SIS模型')初始条件为人数 N=10000 ,初始感染者 I=1 ,每天闲逛到处溜达接触的人数是 r=10 ,接触后传染的概率为 b=0.01 ,中招后康复的概率为 ![]() 。
。
最终生病和健康的人数形成了一个稳定的动态平衡。
SIR模型
我们继续增加模型复杂度,人在康复以后产生了抗体就不会再得病。不同于SIS模型,我们在模型中引入康复者(The Recovered),用 R 表示,并满足总人数 N=S+I+R 。这个时候就是SIR模型。一旦变为康复者,就不会再传染,即在概率传递过程中,一旦变为康复者,就没有概率再次转移为感染者或者易感者。我们假设感染者变为康复者的概率为我们来看下SIR模型的微分方程
仿真代码如下
%--------------------------------------------------------------------------
% 初始化
%--------------------------------------------------------------------------
clear;clc;
%--------------------------------------------------------------------------
% 参数设置
%--------------------------------------------------------------------------
N = 10000; %人口总数
I = 1; %传染者
S = N - I; %易感者
R = 0; %康复者
r = 10; %感染者接触易感者的人数
B = 0.05; %传染概率
y = 0.1; %康复概率
T = 1:100;
for idx = 1:length(T)-1
S(idx+1) = S(idx) - r*B*S(idx)*I(idx)/N;
I(idx+1) = I(idx) + r*B*S(idx)*I(idx)/N - y*I(idx);
R(idx+1) = R(idx) + y*I(idx);
end
plot(T,S,T,I,T,R);grid on;
xlabel('天');ylabel('人数')
legend('易感者','传染者','康复者')这样子一看我们就发现和现实生活中比较接近了,按照这个参数仿真,在传播初期30天左右会迎来一个峰值,感染人数达到5000人,随着治疗康复的人越来越多,感染者下降,拥有抗体的人数不断增多,病情得到控制,感染者人数减少。
SEIR模型
实际情况更加复杂,易感染人群在一开始会经历潜伏期,一段时间之后才出现症状,因此我们在SIR模型的基础上引入潜伏者E (The Exposed),潜伏者按照概率 ![]() 转化为感染者,在SIR的基础上修改微分方程
转化为感染者,在SIR的基础上修改微分方程
同样,在SIR模型的基础上略微修改代码就得到了SEIR模型
%--------------------------------------------------------------------------
% 初始化
%--------------------------------------------------------------------------
clear;clc;
%--------------------------------------------------------------------------
% 参数设置
%--------------------------------------------------------------------------
N = 10000; %人口总数
E = 0; %潜伏者
I = 1; %传染者
S = N - I; %易感者
R = 0; %康复者
r = 20; %感染者接触易感者的人数
B = 0.03; %传染概率
a = 0.1; %潜伏者转化为感染者概率
y = 0.1; %康复概率
T = 1:140;
for idx = 1:length(T)-1
S(idx+1) = S(idx) - r*B*S(idx)*I(idx)/N;
E(idx+1) = E(idx) + r*B*S(idx)*I(idx)/N-a*E(idx);
I(idx+1) = I(idx) + a*E(idx) - y*I(idx);
R(idx+1) = R(idx) + y*I(idx);
end
plot(T,S,T,E,T,I,T,R);grid on;
xlabel('天');ylabel('人数')
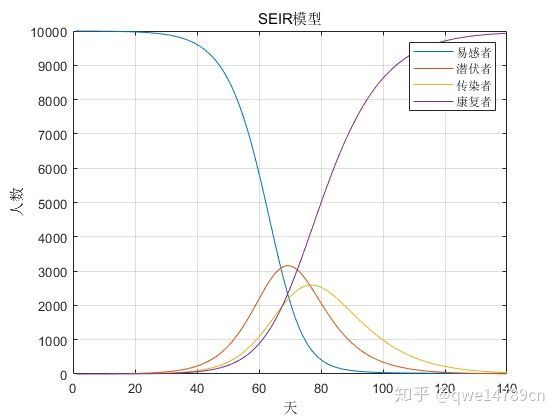
legend('易感者','潜伏者','传染者','康复者')我们看到潜伏者数量也是先增加再减少。
修改后的SEIR模型
现在已经比较接近真实情况了,但是我们看到这次的病毒潜伏期具有传染性(前面的潜伏者只是正常的人通过接触患者变成潜伏者,而实际上,潜伏者和正常人接触后也可能让正常人变成潜伏者),因此我们要引入潜伏者的传染概率 ![]() 可以将健康的易感者转变为潜伏者。而潜伏者每天接触的健康易感者人数为
可以将健康的易感者转变为潜伏者。而潜伏者每天接触的健康易感者人数为 ![]() 。
。
代码如下:
%--------------------------------------------------------------------------
% 初始化
%--------------------------------------------------------------------------
clear;clc;
%--------------------------------------------------------------------------
% 参数设置
%--------------------------------------------------------------------------
N = 10000; %人口总数
E = 0; %潜伏者
I = 1; %传染者
S = N - I; %易感者
R = 0; %康复者
r = 20; %感染者接触易感者的人数
B = 0.03; %传染概率
a = 0.1; %潜伏者转化为感染者概率
r2 = 20; %潜伏者接触易感者的人数
B2 = 0.03; %潜伏者传染正常人的概率
y = 0.1; %康复概率
T = 1:140;
for idx = 1:length(T)-1
S(idx+1) = S(idx) - r*B*S(idx)*I(idx)/N(1) - r2*B2*S(idx)*E(idx)/N;
E(idx+1) = E(idx) + r*B*S(idx)*I(idx)/N(1)-a*E(idx) + r2*B2*S(idx)*E(idx)/N;
I(idx+1) = I(idx) + a*E(idx) - y*I(idx);
R(idx+1) = R(idx) + y*I(idx);
end
plot(T,S,T,E,T,I,T,R);grid on;
xlabel('天');ylabel('人数')
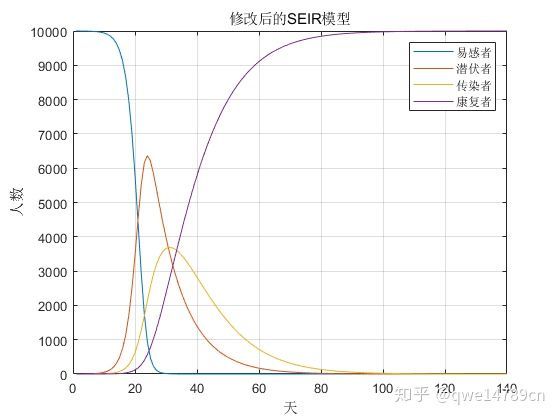
legend('易感者','潜伏者','传染者','康复者')我们发现潜伏者一旦可以感染,人数爆发期大幅度提前,那么如果我们都在家宅怎么办?
我们假设在第10天的时候,命令下发,不要闲逛。
那么这时候将感染者接触健康易感人群人数 r=5,潜伏者接触健康易感人群人数是r2=5。我们在代码中加入if条件,修改接触人数:
%--------------------------------------------------------------------------
% 初始化
%--------------------------------------------------------------------------
clear;clc;
%--------------------------------------------------------------------------
% 参数设置
%--------------------------------------------------------------------------
N = 10000; %人口总数
E = 0; %潜伏者
I = 1; %传染者
S = N - I; %易感者
R = 0; %康复者
r = 20; %感染者接触易感者的人数
B = 0.03; %传染概率
a = 0.1; %潜伏者转化为感染者概率
r2 = 20; %潜伏者接触易感者的人数
B2 = 0.03; %潜伏者传染正常人的概率
y = 0.1; %康复概率
T = 1:140;
for idx = 1:length(T)-1
if idx>=10
r=5;
r2=5;
end
S(idx+1) = S(idx) - r*B*S(idx)*I(idx)/N(1) - r2*B2*S(idx)*E(idx)/N;
E(idx+1) = E(idx) + r*B*S(idx)*I(idx)/N(1)-a*E(idx) + r2*B2*S(idx)*E(idx)/N;
I(idx+1) = I(idx) + a*E(idx) - y*I(idx);
R(idx+1) = R(idx) + y*I(idx);
end
plot(T,S,T,E,T,I,T,R);grid on;
hold on
plot([10 10],[0 10000])
xlabel('天');ylabel('人数')
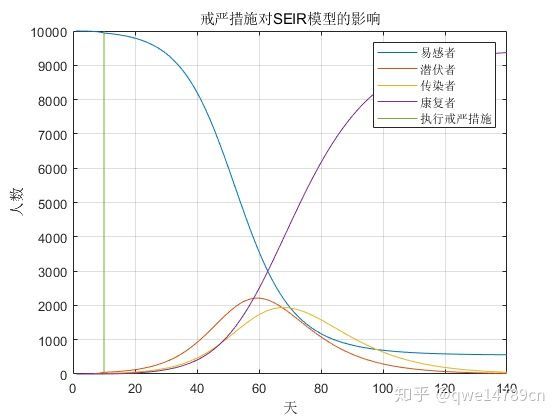
legend('易感者','潜伏者','传染者','康复者','执行戒严措施')
title('戒严措施对SEIR模型的影响')我们可以看到,疾病高发期的时间向后延长和疾病高峰人数大幅下降,这样子为我们抗击肺炎病毒争取了更多的应对时间,并且人数的减少大幅度降低了社会资源的消耗
因此得出结论:
我们在家宅着是可以为抗击疫情做贡献的,大家还是好好听话,不要出去随便穿门走动,要么被村长的广播嘲讽,多丢人哪。玩瘟疫公司去了~溜了溜了