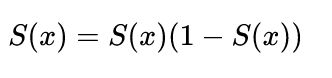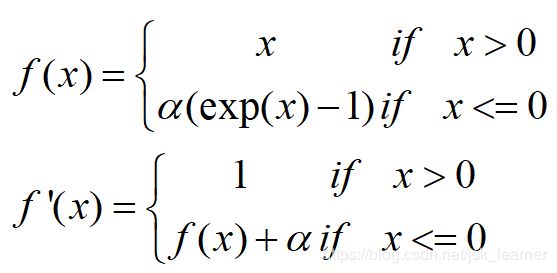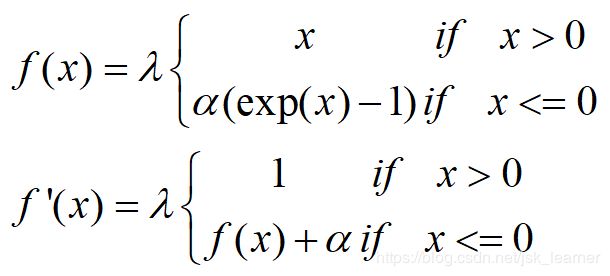深度学习—激活函数详解(Sigmoid、tanh、ReLU、ReLU6及变体P-R-Leaky、ELU、SELU、Swish、Mish、Maxout、hard-sigmoid、hard-swish)
非线性激活函数详解
- 饱和激活函数
- Sigmoid函数
- tanh函数
- hard-Sigmoid函数
- 非饱和激活函数
- Relu(修正线性单元):
- Relu6(抑制其最大值):
- ELU(指数线性单元)
- SELU
- Leaky-Relu / R-Relu
- P-Relu(参数化修正线性单元)
- R-Relu(随机纠正线性单元)
- Swish
- hard-Swish
- Mish
- Maxout
- 关于激活函数统一说明
- 参考链接
因为深度学习模型中其它的层都是线性的函数拟合,即便是用很深的网络去拟合,其还是避免不了线性的特性,无法进行非线性建模,而加入非线性激活函数单元,当线性函数的输出层经过非线性激活单元的时候,其输出呈现一种非线性的变化,这样经过多层的拟合,就可以完成对输入的非线性建模操作。同时还可以起到一种特征组合的作用。
好的激活函数的特征一般应当是平滑的,而且对于负值有较好的处理。
关于本文中的图形绘制请参考我这篇博客:最全面:python绘制Sigmoid、Tanh、Swish、ELU、SELU、ReLU、ReLU6、Leaky ReLU、Mish、hard-Sigmoid、hard-Swish等激活函数(有源码)
饱和激活函数
- 主要是Sigmoid和tanh函数,又加上了hard-Sigmoid函数
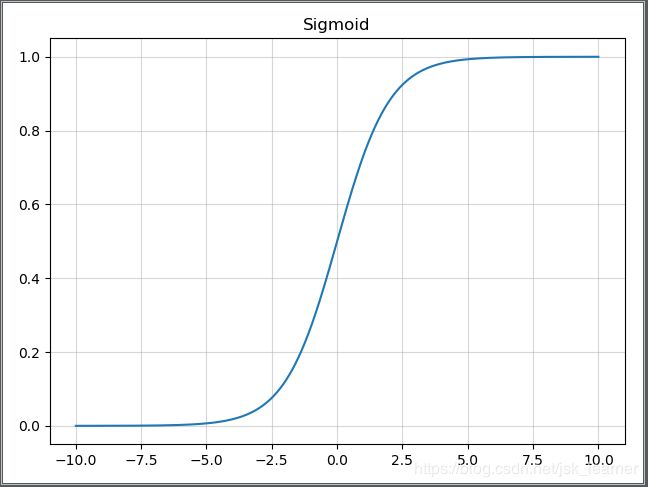
Sigmoid函数
观察Sigmoid函数曲线,可以知道其输出分布在【0,1】区间,而且在输入值较大和较小的情况,其输出值变化都会比较小,仅仅当输入值接近为0时,它们才对输入强烈敏感。Sigmod单元的广泛饱和性会使得基于梯度的学习变得非常困难。因为这个原因,现在已经不鼓励将它们作为前馈网络的隐藏单元。
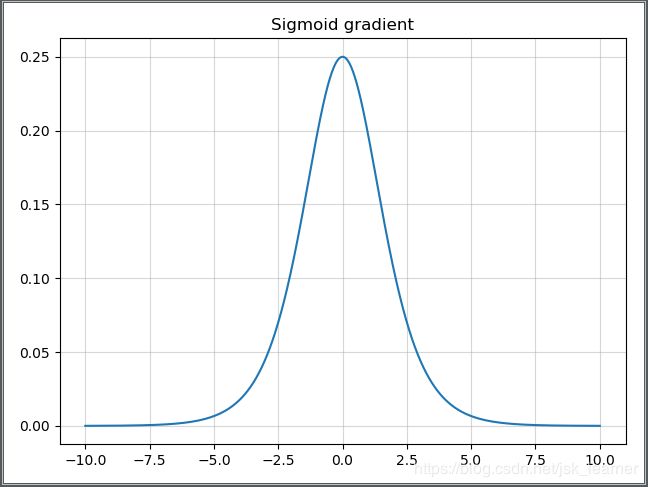
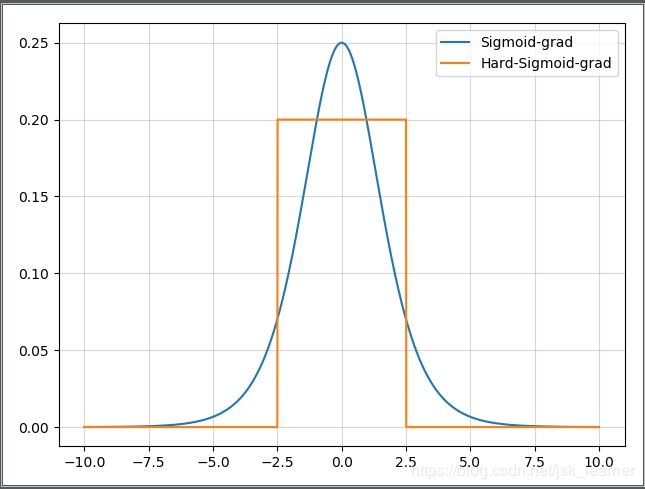
观察Simod导数曲线,呈现一个类似高斯分布的驼峰装,其取值范围在【0,0.25】之间,而我们初始化后的网络权值通常小于1,因此当层数增多时,小于0的值不断相乘,最后就会导致梯度消失的情况出现。而梯度爆炸则是当权值过大,导致其导数大于1,大于1的数不断相乘,发生梯度爆炸。
同时Sigmoid还有其他缺点,如输出不是以0为中心,而是0.5,这样在求解权重的梯度时,梯度总是正或负的,指数计算耗时。
总之不推荐使用sigmoid饱和激活函数。
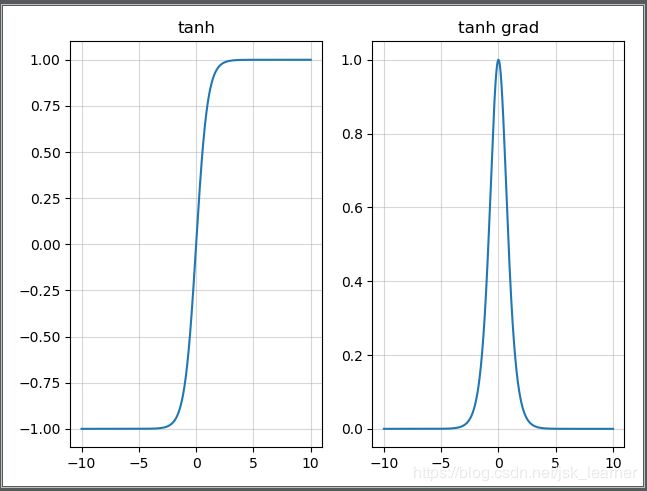
tanh函数
公式:
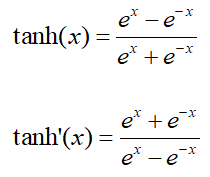
不过sigmoid和tanh在RNN(LSTM、注意力机制等)结构上有所应用,作为门控或者概率值。
这里关于tanh为什么比simoid收敛快有一个比较好的说法,引用了以下说法:
梯度消失问题程度
tanh′(x)=1−tanh(x)2∈(0,1)tanh′(x)=1−tanh(x)2∈(0,1)
sigmoid: s′(x)=s(x)×(1−s(x))∈(0,1/4)sigmoid: s′(x)=s(x)×(1−s(x))∈(0,1/4)
可以看出tanh(x)的梯度消失问题比sigmoid要轻.梯度如果过早消失,收敛速度较慢.
以零为中心的影响
如果当前参数(w0,w1)的最佳优化方向是(+d0, -d1),则根据反向传播计算公式,我们希望 x0 和 x1 符号相反。但是如果上一级神经元采用 Sigmoid 函数作为激活函数,sigmoid不以0为中心,输出值恒为正,那么我们无法进行最快的参数更新,而是走 Z 字形逼近最优解。
hard-Sigmoid函数
公式:
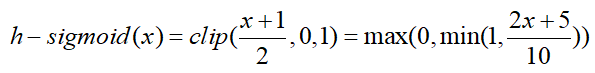
解释:当 x < -2.5输出0,当 x > 2.5时,输出1,当 -2.5 < x & x < 2.5时,输出为 (2x+5) / 10,线性函数。
那么其导数,当 x < -2.5输出0,当 x > 2.5时,输出0,当 -2.5 < x & x < 2.5时,输出为 1 / 5。
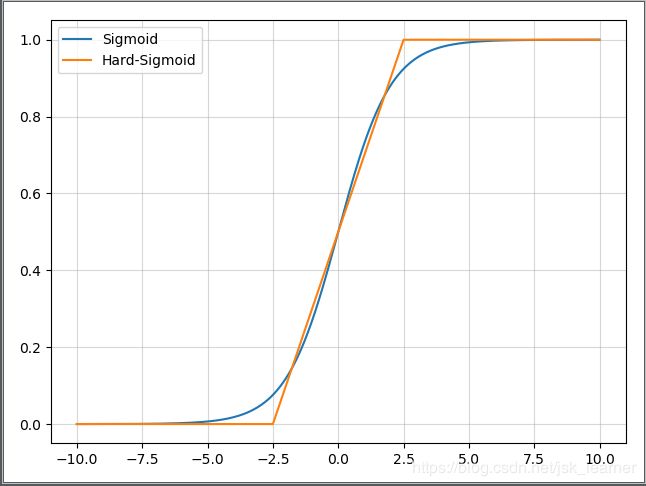
hard-Sigmoid函数时Sigmoid激活函数的分段线性近似。从公示和曲线上来看,其更易计算,因此会提高训练的效率,不过同时会导致一个问题:就是首次派生值为零可能会导致神经元died或者过慢的学习率。
- Sigmoid函数和hard-Sigmoid函数对比图:
非饱和激活函数
- Sigmod和tanh都是饱和激活函数,即两者在输入值较大或较小的时候对输入值不再那么敏感。
而以Relu及其变体为代表的一类非饱和激活函数在防止梯度消失方面具有无可比拟的优势,现如今基本很少在网络中使用Sigmod等饱和激活函数。
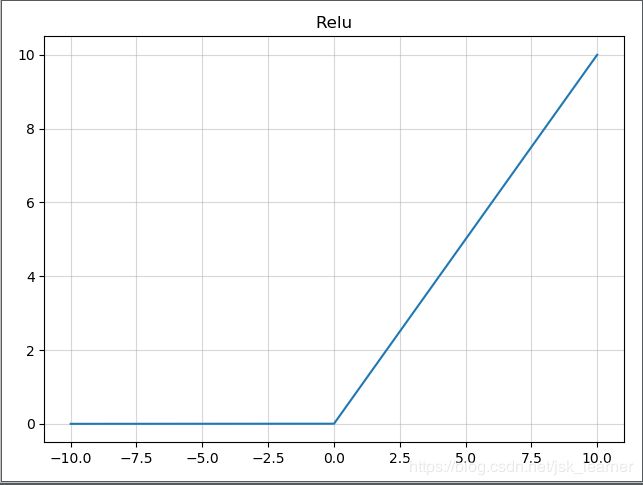
Relu(修正线性单元):
将所有的负值置为0,而其余的值不变。
缺点:一个很大的梯度流过一个Relu神经元,更新过梯度后,那么这个神经元对大部分数据都没有激活作用了,因此梯度就是0。会造成神经元的死亡。

Relu6(抑制其最大值):
- 公式:
- 目的:
主要是为了在移动端float16的低精度的时候,也能有很好的数值分辨率,如果对ReLu的输出值不加限制,那么输出范围就是0到正无穷,而低精度的float16无法精确描述其数值,带来精度损失。
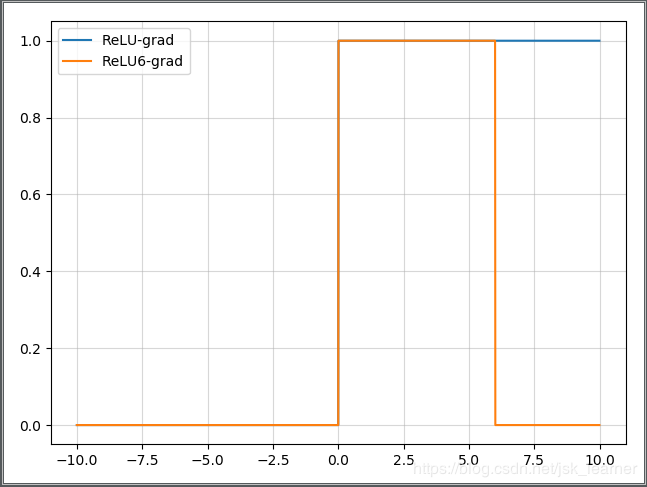
- ReLU和ReLU6图表对比:
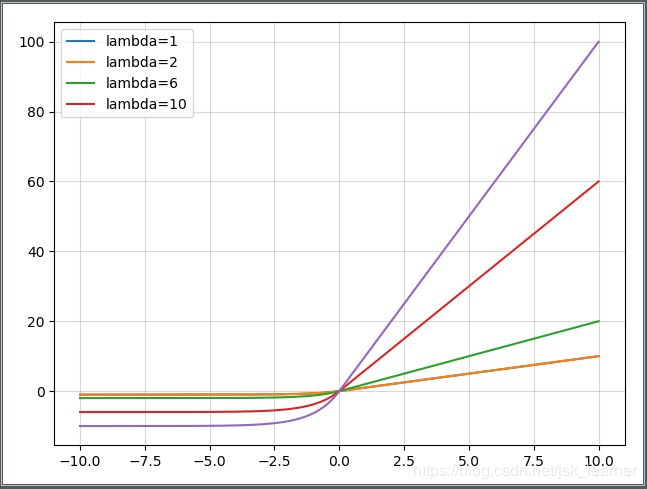
ELU(指数线性单元)
其将激活函数的平均值接近零,从而加快学习的速度。同时,还可以通过正值的标识来避免梯度消失的问题。根据一些研究,ELU的分类 精确度要高于Relu。
-
融合了sigmoid和ReLU,左侧具有软饱和性,右侧无饱和性。
-
右侧线性部分使得ELU能够缓解梯度消失,而左侧软饱能够让ELU对输入变化或噪声更鲁棒。
-
ELU的输出均值接近于零,所以收敛速度更快。
-
在 ImageNet上,不加 Batch Normalization 30 层以上的 ReLU
网络会无法收敛,PReLU网络在MSRA的Fan-in (caffe )初始化下会发散,而 ELU
网络在Fan-in/Fan-out下都能收敛。
SELU
就是给ELU乘上一个系数,该系数大于1。
在这篇paper Self-Normalizing Neural Networks中,作者提到,SELU可以使得输入在经过一定层数之后变为固定的分布。
以前的ReLU、P-ReLU、ELU等激活函数都是在负半轴坡度平缓,这样在激活的方差过大时可以让梯度减小,防止了梯度爆炸,但是在正半轴其梯度简答的设置为了1。而SELU的正半轴大于1,在方差过小的时候可以让它增大,但是同时防止了梯度消失。这样激活函数就有了一个不动点,网络深了之后每一层的输出都是均值为0,方差为1.
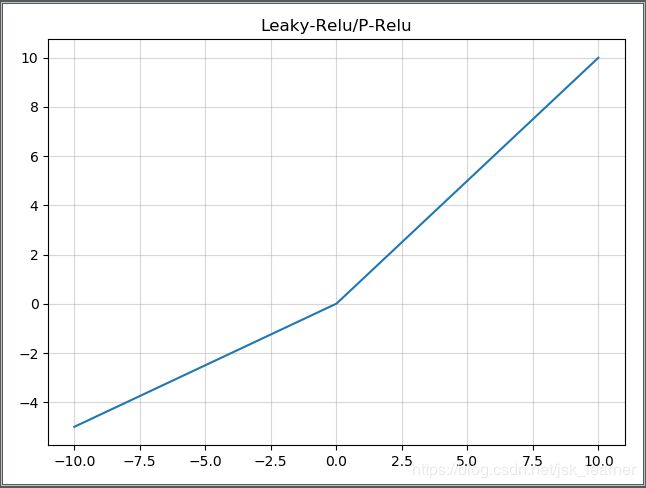
Leaky-Relu / R-Relu
Leaky ReLU和ReLU不同的是,ReLU是将所有的负值设为零,而Leaky ReLU是给所有负值赋予一个非零斜率,即用一个负值部分除以大于1的数。(公式中a是大于1的一个常数)
P-Relu(参数化修正线性单元)
可以看作是Leaky ReLU的一个变体,不同的是,P-ReLU中的负值部分的斜率是根据数据来定的,即a的值并不是一个常数。
R-Relu(随机纠正线性单元)
R-ReLU也是Leaky ReLU的一个变体,只不过在这里负值部分的斜率在训练的时候是随机的,即在一个范围内随机抽取a的值,不过这个值在测试环节会固定下来。
Swish
paper : Searching for Activation Functions
beta是个常数或者可以训练的参数。其具有无上界有下界、平滑、非单调的特性。其在模型效果上优于ReLU。
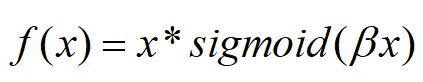
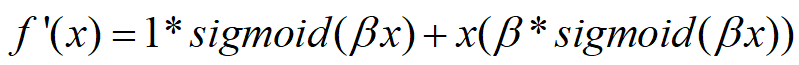
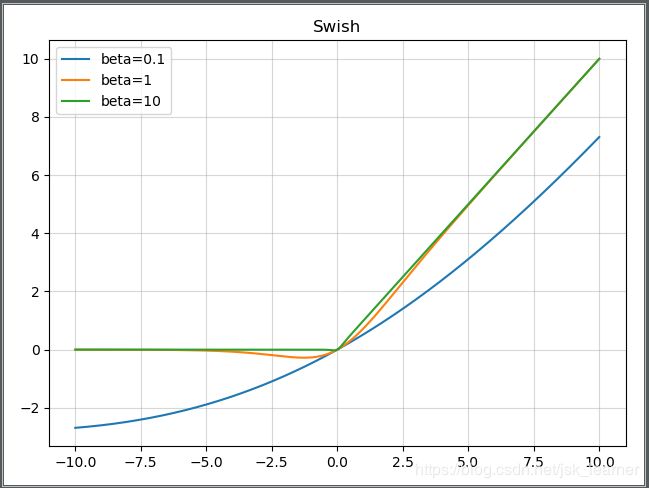
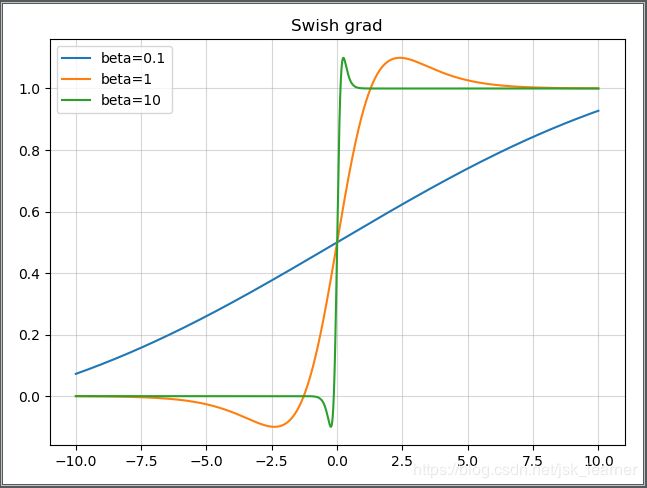
当β = 0时,Swish变为线性函数f(x)=x2f(x)=x2.
β → ∞, σ(x)=(1+exp(−x))−1σ(x)=(1+exp(−x))−1为0或1. Swish变为ReLU: f(x)=2max(0,x)
所以Swish函数可以看做是介于线性函数与ReLU函数之间的平滑函数.
hard-Swish
paper: Searching for MobileNetV3
- 公式:

在论文中,作者提到,虽然这种Swish非线性提高了精度,但是在嵌入式环境中,他的成本是非零的,因为在移动设备上计算sigmoid函数代价要大得多。
因此作者使用hard-Swish和hard-Sigmoid替换了ReLU6和SE-block中的Sigmoid层,但是只是在网络的后半段才将ReLU6替换为h-Swish,因为作者发现Swish函数只有在更深的网络层使用才能体现其优势。
首先是肯定了Swish的重要性,然后指出在量化模式下,Sigmoid函数比ReLU6的计算代价大的多,所以才有了这个ReLU6版本的h-Swish。
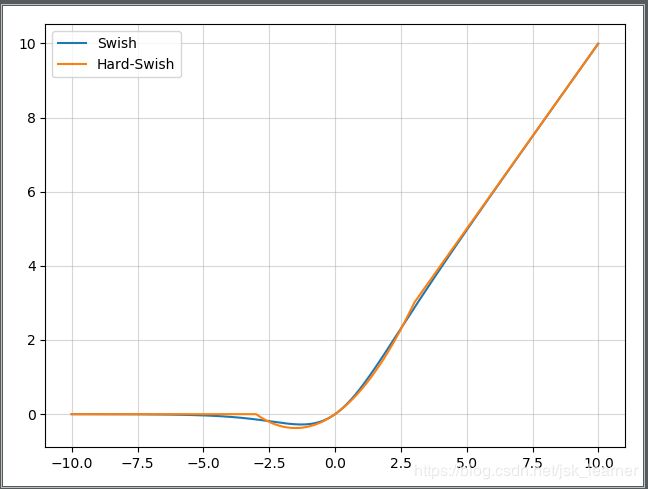
- Swish和hard-Swish图表对比:
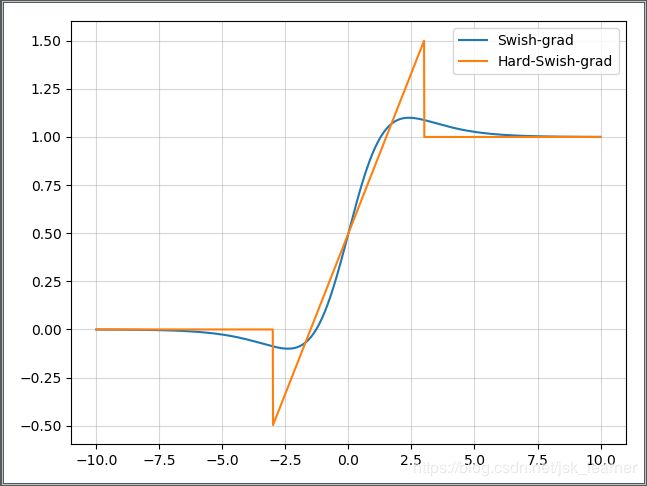
关于hard-Swish的梯度图我不确定有没有画错,如果有错误还请指正,谢谢。
Mish
Mish: A Self Regularized Non-Monotonic Neural Activation Function
这篇应该是笔者写时关于激活函数改进的最新一篇文章。
相比Swish有0.494%的提升,相比ReLU有1.671%的提升。
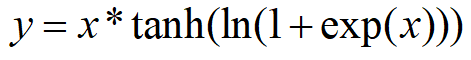
关于公式及其导数推导如下图所示:

Mish和Swish中参数=1的曲线对比:(第一张是原始函数,第二张是导数)
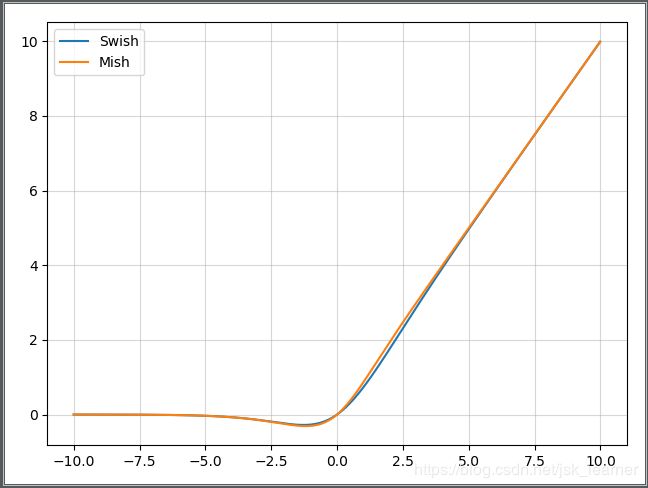
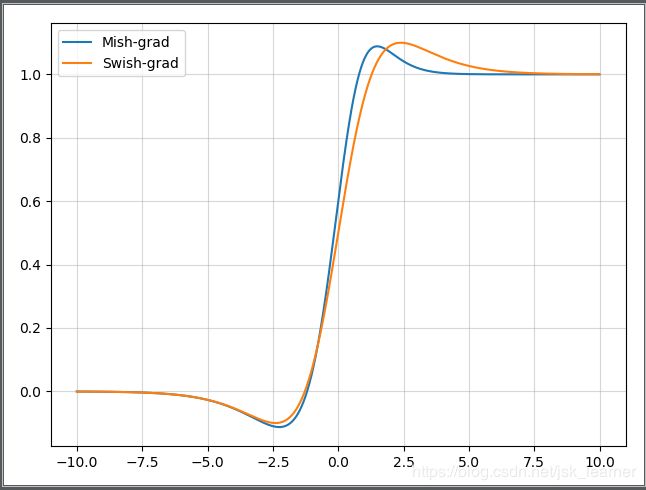
为什么Mish表现的更好:
以上无边界(即正值可以达到任何高度)避免了由于封顶而导致的饱和。理论上对负值的轻微允许允许更好的梯度流,而不是像ReLU中那样的硬零边界。
最后,可能也是最重要的,目前的想法是,平滑的激活函数允许更好的信息深入神经网络,从而得到更好的准确性和泛化。
要区别可能是Mish函数在曲线上几乎所有点上的平滑度
Maxout
paper:Maxout Networks
与常规的激活函数不同,Maxout是一个可以学习的分段线性函数。
其可以看做是在深度学习网络中加入了一层激活函数层,包含一个参数k,这一层相比ReLU,Sigmoid等,其在于增加了k个神经元,然后输出激活值最大的值。
其需要学习的参数就是k个神经元中的权值和偏置,这就相当于常规的激活函数一层,而Maxout是两层,而且参数个数增加了K倍。
其可以有效的原理是,任何ReLU及其变体等激活函数都可以看成分段的线性函数,而Maxout加入的一层神经元正是一个可以学习参数的分段线性函数。
优点:其拟合能力很强,理论上可以拟合任意的凸函数;
具有ReLU的所有优点,线性和非饱和性;
同时没有ReLU的一些缺点,如神经元的死亡;
缺点:导致整体参数的激增。
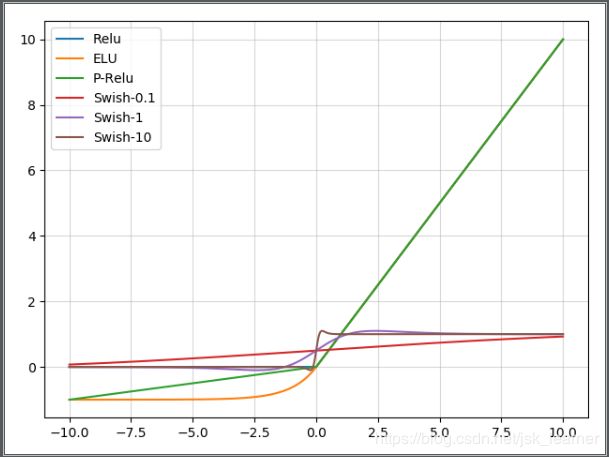
下图非自制:
关于激活函数统一说明
ELU在正半轴取输入x奸情了梯度弥散情况(正半轴导数处处为1),而这一点特性,基本上除了swish其他非饱和激活函数都具有这个特性。而只有ReLU在负半轴的输出没有复制,所以ReLU的输出均值一定是大于0的,而当激活值的均值非0时,会对下一层造成以bias,也就是下一层的激活单元会出现bias shift现象,通过不断的层数叠加,bias shift会变得非常大。而ELU可以让激活函数的输出均值尽可能接近0,类似于BN操作,但是计算复杂度更低。而且虽然Leaky ReLU和PReLU等都有负值,但是它们不保证在不激活的状态对噪声鲁棒,这里的不激活指的是负半轴。而ELU在输入取较小值时具有软饱和的特性,提升了对噪声的鲁棒性。Swish和ELU都是可以取负值,同时在负半轴具有软饱和的性能,提高了对噪声的鲁棒性,SELU效果比ELU效果还要更好。
参考链接
ELU激活函数的提出
激活函数(ReLU, Swish, Maxout)
激活函数ReLU、Leaky ReLU、PReLU和RReLU
2019.10.30.
希望能帮到你。点赞是对我最大的认可。谢谢。