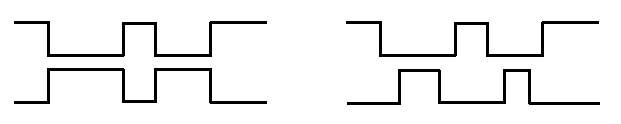电机控制基础 --- (3)
作者:Stephen Du
免责声明: 本文为个人学习笔记及总结,仅代表个人观点,尽可能保证内容准确性。复制/转发请注明来源/作者。
欢迎添加微信交流学习。
接上一篇继续
文章目录
- 3. FOC(Field Oriented Control)
- 3.1 什么是FOC
- 3.2 Clarke/Park变换
- 3.2.1 Clarke变换
- 3.2.2 Park变换
- 3.3 FOC整体控制思想
- 3.4 弱磁
- 3.4.1 弱磁原理
- 3.4.2 恒转矩及恒功率区域
- 3.4.3 弱磁常见方法
- 3.4.4 最大弱磁速度
- 3.4.5 弱磁适用场景
- 3.4.6 是否可以弱磁
- 3.4.7 直轴反电动势
- 3.4.8 反电动势作用
- 3.5 初始位置检测(IPD)
- 3.6 位置检测---观测器
- 3.7 堵转检测
- 4. 常见问题
- 4.1 PWM要求
- 4.1.1 计算占空比的时候是否要包含死区时间?
- 4.1.2 死区时间怎么个加法?
- 4.1.3 会不会出现一路为低(高)电平,另一路有一个很窄的脉冲?
3. FOC(Field Oriented Control)
3.1 什么是FOC
前文我们已经讲过,要让电机稳定高效的转起来,定子上的旋转磁场不能快,也不能慢,那到底要什么样的速度才好,我们以什么为判断标准呢?
回到图1.5,我们想想,转的慢了,定子和转子的两个磁极距离小,这时候力量大,转子可以跟上,但是没有发挥最大优势,可以再快点。如果太快了,两个磁极距离太大,力就变小了,容易跟不上。我们发现,其实也就力和距离两个东西,我们只要平衡好就行。注意这里的距离其实包含了两个东西,一个是我们说的两个磁极之间距离,这个距离会影响力的大小。还有一个隐含的距离,那就是转子的半径,这个距离是什么?这是产生转矩的距离,因为转子转起来的本质是因为什么?不是说是力么?没错,是力,但准确的说是因为有转矩,光有力,用错方向也白费功夫。你想想,两个磁极对齐的时候也有力,并且这个力是最大的,但是这时候转不起来,因为转矩为0。转矩(力矩)就是力和距离的乘积,在电机系统里面,距离就是转子的半径,这是固定不变的,那归根结底我们还是只需要控制好力就行了。为了方便分析,我们将受力图画出来。如下图所示:
定子和转子上的磁铁都会产生磁场,两个磁场叠加,共同产生作用,转矩正比于图中矢量所围成的面积或者说正比于两个磁场矢量的叉乘。假如两个磁极对齐,面积为0,没有力(注意这里说没有力不是说两个磁极之间没力,而是说没有让转子转动的有效力)。当两个磁极成90°垂直时,面积最大,力最大。这比较好理解。现在问题就变成来处理这两个矢量了,于是这种方法就叫做矢量控制(Vector Control)。这两个矢量是什么?是磁场,所以也叫FOC(Field Oriented Control)。
3.2 Clarke/Park变换
可惜图3.1是我们简化的模型,定子和转子上都是抽象的磁铁,其磁感应强度是固定的,我们可以通过一些简单测试或理论公式便可得到不同位置的力的大小来算出转矩,也可以轻易的画出图中的两个矢量进行分析。但是别忘了,真实电机里面是变化的三相交流电,它的变化还不是简单的线性变化,而是三角函数,并且实际电机中由于绕线等原因,产生的磁场并不是均匀的(在齿上磁通大,气隙小,齿槽的地方气隙大,磁通小)。也就是说定子上的磁极自己的磁感应强度也是变化的,现在有多个变化量,是不是头大了。但不管怎样,我们的目标很明确了,就是找到力和距离的最优组合,或者说根据不同位置来控制好电流大小/磁感应强度。
为了解决上面的问题,牛人就发明了Clarke/Park变换,它的本质就是为了简化我们探索力在不同空间位置与输入信号的关系的处理方法,将上面说的多变量降维或解耦,这样处理起来就会简单很多。如果你还不理解,我们举个例子,这就和我们解一个方程组一样,先用一个变量去等效表示另外一个变量,然后这个式子中就只有一个变量了,这样就可以轻易求解,然后用同样的方法一一求解其他变量,这个过程其实就是降维。但变量替换表达的时候必须注意一个条件,那就是等效。
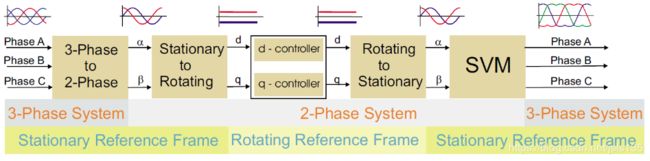
我们先看一下FOC里面各种坐标变换的整体流程:
上图中A/B/C三相到α/β两相的转换就是克拉克(Clarke)变换,由α/β到d/q的转换就是帕克(Park)变换,dq以后的变换是前面的反变换(还原)。
前文已经讲过,电机能转是因为定子绕组里通入的ABC三相交流电产生的磁场是旋转的,那是不是必须三相的交流电才能产生旋转磁场呢?肯定不是,理论上只要大于等于两相的任意对称多项绕组,只要通入多项电流,都可以产生旋转磁场。既然这样,如果我们找一个两相绕组,让它们在空间上相差90°,再通入相差为90°的两项交流电,只要我们保证它的磁场的旋转速度以及产生的磁动势大小一样,那就可以等效三相系统。研究两相系统比三相系统就简单很多,这就是前面说的的降维。
现在的确简单一些,但是我们前面说的多变量还是没解决掉,变成两项后任然是交流电,这就是继续引入Park变换的原因,Park变换将两项交流电变换为两项直流电,这样处理起来就方便了。怎么变成直流电的?怎么保证等效?前面的三项及变换后的两项坐标系都是静止的。Park变换巧妙地将变化的元素移到坐标系本身上面,让静止的α/β坐标系以交流电的旋转频率动起来,那坐标系上的量就是直流(静止)了,这就是一个相对运动的概念。这就是我们前面章节简化模型里面说的让外面整个环动起来,但是环上磁铁大小及相对于环的位置固定(我们假设用磁铁大小来代表磁感应强度的)。转换后的旋转直流绕组和之前的固定交流绕组是等效的。
3.2.1 Clarke变换
接下来我们深入看看Clarke怎么把A/B/C三相变到到α/β两相的呢?如下图所示:
上图中abc坐标系是一个平面坐标,各轴相差120°(因为输入信号abc三相是一个相位差为120°的交流信号),不要习惯性看成三维坐标系了。
其实也就是将合成矢量V在分别在abc坐标及αβ坐标系下表示。这个不难,我们可以直接写出转换公式:
{ i α = k ( i a − cos ( π / 3 ) i b − cos ( π / 3 ) i c ) i β = k ( sin ( π / 3 ) i b − sin ( π / 3 ) i c ) \begin{cases} i_\alpha = k(i_a - &\cos(\pi/3)i_b - \cos(\pi/3)i_c)\\ i_\beta = k(&\sin(\pi/3)i_b - \sin(\pi/3)i_c) \end{cases} {iα=k(ia−iβ=k(cos(π/3)ib−cos(π/3)ic)sin(π/3)ib−sin(π/3)ic)
{ u α = k ( u a − cos ( π / 3 ) u b − cos ( π / 3 ) u c ) u β = k ( sin ( π / 3 ) u b − sin ( π / 3 ) u c ) \begin{cases} u_\alpha = k(u_a - &\cos(\pi/3)u_b - \cos(\pi/3)u_c)\\ u_\beta = k(&\sin(\pi/3)u_b - \sin(\pi/3)u_c) \end{cases} {uα=k(ua−uβ=k(cos(π/3)ub−cos(π/3)uc)sin(π/3)ub−sin(π/3)uc)
转换矩阵如下:
[ i α i β ] = k [ 1 − 1 2 − 1 2 0 3 2 − 3 2 ] [ i a i b i c ] \begin{bmatrix} i_\alpha\\ i_\beta \end{bmatrix}= k\begin{bmatrix} 1 &-\frac{1}{2} &-\frac{1}{2}\\ 0 &\frac{\sqrt3}{2} &-\frac{\sqrt3}{2} \end{bmatrix} \begin{bmatrix} i_a\\ i_b\\ i_c \end{bmatrix} [iαiβ]=k[10−2123−21−23]⎣⎡iaibic⎦⎤
[ u α u β ] = k [ 1 − 1 2 − 1 2 0 3 2 − 3 2 ] [ u a u b u c ] \begin{bmatrix} u_\alpha\\ u_\beta \end{bmatrix}= k\begin{bmatrix} 1 &-\frac{1}{2} &-\frac{1}{2}\\ 0 &\frac{\sqrt3}{2} &-\frac{\sqrt3}{2} \end{bmatrix} \begin{bmatrix} u_a\\ u_b\\ u_c \end{bmatrix} [uαuβ]=k[10−2123−21−23]⎣⎡uaubuc⎦⎤
在abc坐标系下,合成矢量iv和abc三轴的分量还可以表示为下面关系式:
{ i a = i v cos ( ω t ) i b = i v cos ( ω t − 2 π / 3 ) i c = i v cos ( ω t + 2 π / 3 ) \begin{cases} i_a=i_v\cos(\omega t)\\ i_b=i_v\cos(\omega t-2\pi/3)\\ i_c=i_v\cos(\omega t+2\pi/3)\\ \end{cases} ⎩⎪⎨⎪⎧ia=ivcos(ωt)ib=ivcos(ωt−2π/3)ic=ivcos(ωt+2π/3)
{ u a = u v cos ( ω t + φ ) u b = u v cos ( ω t − 2 π / 3 + φ ) u c = u v cos ( ω t + 2 π / 3 + φ ) \begin{cases} u_a=u_v\cos(\omega t+\varphi)\\ u_b=u_v\cos(\omega t-2\pi/3+\varphi)\\ u_c=u_v\cos(\omega t+2\pi/3+\varphi)\\ \end{cases} ⎩⎪⎨⎪⎧ua=uvcos(ωt+φ)ub=uvcos(ωt−2π/3+φ)uc=uvcos(ωt+2π/3+φ)
公式8里面的常数k,根据不同变换方式k的取值不一样,Clarke变换通常又分为等幅变换和等功率变换。
先给结论:
等幅变换: k = 2 3 k=\frac{2}{3} k=32 等功率变换: k = 2 3 k=\sqrt{\frac{2}{3}} k=32
接下来分别介绍推导这两种情况下k的取值。
Clarke — 等幅变换:
等幅变换这里的幅到底指电流的幅还是电压的幅?
查阅资料后也没有明确的结果,大部分资料认为是电流,也有说是电压,个人理解的似乎两个都可以。
因为电机控制应遵循磁势(电流与线圈匝数的乘积)不变,所以指电流,虽然磁场是电流产生的,他们关系的确非常紧密,但电流是电压产生的,所以我理解在这个幅值问题上两者都可以。
等幅变换应满足:
i α 2 + i β 2 = i v \sqrt{{i_\alpha^2}+{i_\beta^2}}=i_v iα2+iβ2=iv
将公式12带入公式8得到:
{ i α = k ( i a − 1 2 i b − 1 2 i c ) = k ∗ 3 2 i v c o s ( ω t ) i β = k ( i a + 3 2 i b − 3 2 i c ) = k ∗ 3 2 i v s i n ( ω t ) \begin{cases} i_\alpha=k(i_a-\frac{1}{2}i_b-\frac{1}{2}i_c)=k*\frac{3}{2}i_vcos(\omega t)\\ i_\beta=k(i_a+\frac{\sqrt3}{2}i_b-\frac{\sqrt3}{2}i_c)=k*\frac{3}{2}i_vsin(\omega t) \end{cases} {iα=k(ia−21ib−21ic)=k∗23ivcos(ωt)iβ=k(ia+23ib−23ic)=k∗23ivsin(ωt)
将公式15带入公式14得到: k = 2 3 k=\frac{2}{3} k=32
Clarke — 等功率变换:
变换前电压方程为:u = Zi(Z是阻抗)
假设电压、电流变换矩阵分别为Cu、Ci,则变换前后的电压、电流关系式为(u’,i’为变换后电压及电流):
{ u = C u ∗ u ′ i = C i ∗ i ′ \begin{cases} u = C_u*u'\\ i = C_i*i' \end{cases} {u=Cu∗u′i=Ci∗i′
要使变换前后功率不变,则:P = iT*u = i’T*u’,得到:CiT*Cu = E
我们为了计算方便,简化/统一变换矩阵,一般取Cu = Ci = C,也就是CT*C = E或者说CT = C-1。
C是一个正交矩阵(存在逆矩阵C-1,肯定是方阵,其秩不为0,因为C在电压等式中代表阻抗,也不能为0)。
CT: C的转置矩阵 C-1: C的逆矩阵 E: 单位矩阵
常用矩阵运算法则:
C-1C = E
(Ci’)T = iT’CT
(kC)T = kCT
如果:u = Cu’ 则: u’ = C-1u
前面我们已经说过,电机控制里面应遵循磁势等效,我们将前面等幅变换的公式换个写法,等幅变换里面的k到底代表什么呢?其实是线圈的匝数比。因为磁势是电流和匝数的乘积,那么我可以得到下面的公式:
{ N 2 i α = N 3 i a − N 3 cos ( π / 3 ) i b − N 3 cos ( π / 3 ) i c N 2 i β = N 3 sin ( π / 3 ) i b − N 3 sin ( π / 3 ) i c \begin{cases} N_2i_\alpha = N_3i_a - &N_3\cos(\pi/3)i_b - N_3\cos(\pi/3)i_c\\ N_2i_\beta = &N_3\sin(\pi/3)i_b - N_3\sin(\pi/3)i_c \end{cases} {N2iα=N3ia−N2iβ=N3cos(π/3)ib−N3cos(π/3)icN3sin(π/3)ib−N3sin(π/3)ic
变换矩阵则为:
[ i α i β ] = N 3 N 2 [ 1 − 1 2 − 1 2 0 3 2 − 3 2 ] [ i a i b i c ] \begin{bmatrix} i_\alpha\\ i_\beta \end{bmatrix}= \frac{N_3}{N_2}\begin{bmatrix} 1 &-\frac{1}{2} &-\frac{1}{2}\\ 0 &\frac{\sqrt3}{2} &-\frac{\sqrt3}{2} \end{bmatrix} \begin{bmatrix} i_a\\ i_b\\ i_c \end{bmatrix} [iαiβ]=N2N3[10−2123−21−23]⎣⎡iaibic⎦⎤
我们说了这个C是一个正交矩阵,是一个方正,但是上面这个是一个2x3的矩阵,我们需要引入一个零轴电流i0,这个零轴同时垂直于α和β轴,形成一个新的坐标系,且满足下面等式(k’是待定系数):
N 2 i 0 = k ′ ( N 3 i a + N 3 i b + N 3 i c ) N_2i_0 =k'(N_3i_a + N_3i_b + N_3i_c) N2i0=k′(N3ia+N3ib+N3ic)
i 0 = N 3 N 2 k ′ ( i a + i b + i c ) i_0 =\frac{N_3}{N_2}k'(i_a + i_b + i_c) i0=N2N3k′(ia+ib+ic)
公式18可写为:
[ i α i β i 0 ] = N 3 N 2 [ 1 − 1 2 − 1 2 0 3 2 − 3 2 k ′ k ′ k ′ ] [ i a i b i c ] \begin{bmatrix} i_\alpha\\ i_\beta\\ i_0 \end{bmatrix}= \frac{N_3}{N_2}\begin{bmatrix} 1 &-\frac{1}{2} &-\frac{1}{2}\\ 0 &\frac{\sqrt3}{2} &-\frac{\sqrt3}{2}\\ k'&k'&k' \end{bmatrix} \begin{bmatrix} i_a\\ i_b\\ i_c \end{bmatrix} ⎣⎡iαiβi0⎦⎤=N2N3⎣⎡10k′−2123k′−21−23k′⎦⎤⎣⎡iaibic⎦⎤
则矩阵C为:
C = N 3 N 2 [ 1 − 1 2 − 1 2 0 3 2 − 3 2 k ′ k ′ k ′ ] C = \frac{N_3}{N_2}\begin{bmatrix} 1 &-\frac{1}{2} &-\frac{1}{2}\\ 0 &\frac{\sqrt3}{2} &-\frac{\sqrt3}{2}\\ k'&k'&k' \end{bmatrix} C=N2N3⎣⎡10k′−2123k′−21−23k′⎦⎤
C的转置矩阵CT为:
C T = N 3 N 2 [ 1 0 k ′ − 1 2 3 2 k ′ − 1 2 − 3 2 k ′ ] C^T=\frac{N_3}{N_2}\begin{bmatrix} 1&0&k'\\ -\frac{1}{2}&\frac{\sqrt3}{2}&k'\\ -\frac{1}{2}&-\frac{\sqrt3}{2}&k' \end{bmatrix} CT=N2N3⎣⎢⎡1−21−21023−23k′k′k′⎦⎥⎤
C的逆矩阵C-1为:
C − 1 = 2 N 2 3 N 3 [ 1 0 1 2 k ′ − 1 2 3 2 1 2 k ′ − 1 2 − 3 2 1 2 k ′ ] C^{-1}=\frac{2N_2}{3N_3}\begin{bmatrix} 1&0&\frac{1}{2k'}\\ -\frac{1}{2}&\frac{\sqrt3}{2}&\frac{1}{2k'}\\ -\frac{1}{2}&-\frac{\sqrt3}{2}&\frac{1}{2k'} \end{bmatrix} C−1=3N32N2⎣⎢⎡1−21−21023−232k′12k′12k′1⎦⎥⎤
前面已经推导,要求CT = C-1,也就是: 2 N 2 3 N 3 = N 3 N 2 ; 1 2 k ′ = k ′ \frac{2N_2}{3N_3}=\frac{N_3}{N_2}; \frac{1}{2k'} = k' 3N32N2=N2N3;2k′1=k′。得到 N 3 N 2 = 2 3 ; k ′ = 1 2 \frac{N_3}{N_2}=\sqrt{\frac{2}{3}};k'=\sqrt{\frac{1}{2}} N2N3=32;k′=21
也就是等功率变换是,公式10中的k的取值为: k = 2 3 k=\sqrt{\frac{2}{3}} k=32
使用限制:
什么时候用等幅变换,什么时候用等功率变换?
只要全过程使用一致就行,不要混合使用,总体来说采样等幅变换比较方便,如PWM的标幺化处理比较方便,并且在实际应用中等幅变换对应CPU的要求更低,除非你的硬件有浮点运算器。等功率变换更好理解,大部分教材资料都以等功率变换进行讲解。
3.2.2 Park变换
Park变换继续将两相静止的αβ坐标转换为两相旋转的dq坐标。
描述永磁同步电机三相绕组电压的公式可以用矩阵形式写成如下:
[ u a u b u c ] = R s [ i a i b i c ] + d d t [ ψ a ψ b ψ c ] \begin{bmatrix} u_a \\ u_b \\ u_c \end{bmatrix} = R_s \begin{bmatrix} i_a \\ i_b \\ i_c \end{bmatrix} +\frac{d}{d_t} \begin{bmatrix} \psi_a\\ \psi_b\\ \psi_c \end{bmatrix} ⎣⎡uaubuc⎦⎤=Rs⎣⎡iaibic⎦⎤+dtd⎣⎡ψaψbψc⎦⎤
其中:
[ ψ a ψ b ψ c ] = [ L a a L a b L a c L b a L b b L b c L c a L c b L c c ] [ i a i b i c ] + Ψ P M [ cos ( θ e ) cos ( θ e − 2 π 3 ) cos ( θ e + 2 π 3 ) ] \begin{bmatrix} \psi_a\\ \psi_b\\ \psi_c \end{bmatrix}= \begin{bmatrix} L_{aa} &L_{ab} &L_{ac}\\ L_{ba} &L_{bb} &L_{bc}\\ L_{ca} &L_{cb} &L_{cc} \end{bmatrix} \begin{bmatrix} i_a\\ i_b\\ i_c \end{bmatrix}+\Psi_{PM} \begin{bmatrix} \cos(\theta_e)\\ \cos(\theta_e-\frac{2\pi}{3})\\ \cos(\theta_e+\frac{2\pi}{3}) \end{bmatrix} ⎣⎡ψaψbψc⎦⎤=⎣⎡LaaLbaLcaLabLbbLcbLacLbcLcc⎦⎤⎣⎡iaibic⎦⎤+ΨPM⎣⎡cos(θe)cos(θe−32π)cos(θe+32π)⎦⎤
L a a L_{aa} Laa, L b b L_{bb} Lbb, L c c L_{cc} Lcc:各定子相的自感。
L a b = L b a L_{ab} = L_{ba} Lab=Lba, L b c = L c b L_{bc} = L_{cb} Lbc=Lcb, L c a = L a c Lca = Lac Lca=Lac:各定子相之间的互感。
Ψ P M \Psi_{PM} ΨPM:由转子永磁体产生的磁通量(转子永磁体磁链的最大值 ), Ψ P M cos ( θ e [ ± 2 π 3 ] ) \Psi_{PM}\cos(\theta_e[\pm\frac{2\pi}{3}]) ΨPMcos(θe[±32π])为永磁磁链在各相中的交链。
θ e \theta_e θe:转子电角度。
αβ坐标与dq坐标转换:
如图所示,变换后的dq坐标,由于d轴和q轴上有交叉耦合,q轴上有反电动势电压分量,这是一个非线性交叉相关系统。其表达式如下:
[ u d u q ] = R s [ i d i q ] + [ L d 0 0 L q ] d d t [ i d i q ] + ω e [ 0 − L q L d 0 ] [ i d i q ] + ω e Ψ P M [ 0 1 ] \begin{bmatrix} u_d \\ u_q \end{bmatrix} = R_s \begin{bmatrix} i_d \\ i_q \end{bmatrix} + \begin{bmatrix} L_d&0\\ 0&L_q \end{bmatrix} \frac{d}{d_t} \begin{bmatrix} i_d\\ i_q \end{bmatrix} +\omega_e \begin{bmatrix} 0&-L_q\\ L_d&0 \end{bmatrix} \begin{bmatrix} i_d\\ i_q \end{bmatrix}+\omega_e\Psi_{PM} \begin{bmatrix} 0\\ 1 \end{bmatrix} [uduq]=Rs[idiq]+[Ld00Lq]dtd[idiq]+ωe[0Ld−Lq0][idiq]+ωeΨPM[01]
如上式,后面两部分为耦合项。在FOC中,我们需要对这两项进行补偿,为了简化控制,通常我们将这两项放在状态观测器里进行补偿,这样我们可以对dq电流进行独立控制。 控制方程组如下:
u d = R s i d + L d d i d d t u q = R s i q + L q d i q d t \begin{array}{lcr} u_d=R_si_d+L_d\frac{di_d}{d_t}\\ u_q=R_si_q+L_q\frac{di_q}{d_t} \end{array} ud=Rsid+Lddtdiduq=Rsiq+Lqdtdiq
上面的公式描述了dq电流回路模型,这两个式子在结构上是相同的,所以dq控制器可以采用相同的控制器设计方法。但是dq轴的电感值不一样(通常我们认为表贴式电机dq轴电感一样,而突极/内嵌式电机dq轴电感不一样),这会导致控制器的增益不同。考虑到模型式闭环控制(有反馈),任一等式使用标准PI控制器,然后使用极点配置方法,可以得到控制器的比例增益和积分增益。增益表达式如下:
K p = 2 ξ ω 0 L − R K i = ω 0 2 L \begin{array}{lcr} K_p=2\xi\omega_0L-R\\ K_i=\omega_0^2L \end{array} Kp=2ξω0L−RKi=ω02L
ω0表示系统固有频率[rad/sec],ξ表示电流控制回路的阻尼系数。
由上图,经过几何变换,可得在dq坐标和αβ坐标下的关系式:
{ U d = U α cos ( θ ) + U β sin ( θ ) U q = − U α sin ( θ ) + U β cos ( θ ) \begin{cases} U_d=U_\alpha\cos(\theta)+U_\beta\sin(\theta)\\ U_q=-U_\alpha\sin(\theta)+U_\beta\cos(\theta) \end{cases} {Ud=Uαcos(θ)+Uβsin(θ)Uq=−Uαsin(θ)+Uβcos(θ)
逆变换为:
{ U α = U d cos ( θ ) − U q sin ( θ ) U β = U d sin ( θ ) + U q cos ( θ ) \begin{cases} U_\alpha=U_d\cos(\theta)-U_q\sin(\theta)\\ U_\beta=U_d\sin(\theta)+U_q\cos(\theta) \end{cases} {Uα=Udcos(θ)−Uqsin(θ)Uβ=Udsin(θ)+Uqcos(θ)
上面两个转换对应的矩阵分别为:
[ U d U q ] = [ cos ( θ ) sin ( θ ) − sin ( θ ) cos ( θ ) ] [ U α U β ] [ U α U β ] = [ cos ( θ ) − sin ( θ ) sin ( θ ) cos ( θ ) ] [ U d U q ] \begin{bmatrix} U_d\\ U_q \end{bmatrix}= \begin{bmatrix} \cos(\theta)&\sin(\theta)\\ -\sin(\theta)&\cos(\theta) \end{bmatrix} \begin{bmatrix} U_\alpha\\ U_\beta \end{bmatrix}\\ \begin{bmatrix} U_\alpha\\ U_\beta \end{bmatrix}= \begin{bmatrix} \cos(\theta)&-\sin(\theta)\\ \sin(\theta)&\cos(\theta) \end{bmatrix} \begin{bmatrix} U_d\\ U_q \end{bmatrix} [UdUq]=[cos(θ)−sin(θ)sin(θ)cos(θ)][UαUβ][UαUβ]=[cos(θ)sin(θ)−sin(θ)cos(θ)][UdUq]
3.3 FOC整体控制思想
矢量控制包含很多方法,比如:零直轴电流控制(id=0)/内单位功率因数控制,最大转矩电流比控制(MTPA),弱磁控制,外单位功率因数控制( c o s ϕ = 1 cos\phi=1 cosϕ=1)等。通常一个复杂的控制系统里可能同时包含了多种控制方法。
本文默认以零直轴电流控制进行讲解,如果涉及其他方法会以独立章节进行介绍。零直轴电流控制也叫内单位功率因数控制。零直轴电流控制方法就是在运行过程中,id(直轴)保持为0,单纯控制iq(交轴)。这种控制方法简单,因为id为0,电流矢量幅值等于交轴分量的值,d轴和q轴实现了解耦,电磁转矩的大小只决定于q轴。
平时我们在实际工程中说FOC,大部分时候是一个笼统的说法,它包含了很多技术,比如SVPWM,坐标变换,信号采集反馈,PID控制等,这些统称为FOC控制。如下FOC控制框图所示:
如上图,经过坐标变换后,我们只需要控制id,iq电流大小了,这和控制直流电机一样简单。为了更简单一点,有人提出了零直轴电流控制法(提出这种控制方法是因为有些电机还非常适合使用(见后文))。这样我们就只需要控制iq了。上图中,用户输入一个目标速度值,我们转换为目标电流值(iq)进行控制(step3),step1通过ADC采集abc三相的电流值,然后经过stpe2坐标变换得到id,iq,作为step3中PI调节器的反馈,然后经过step4反变换,得到abc三相输出电压,然后折算到PWM的占空比进行输出控制。
是不是一下这么简单不习惯?
3.4 弱磁
3.4.1 弱磁原理
弱磁控制思想来自于他励直流电机的调磁控制,在它励直流电机应用中,当电机端电压达到最大值以后通过降低电机的励磁电流保证电机电压平衡,从而使电机能够恒功率运行于更高转速。在永磁同步电机中,当电机运行速度达到额定速度后,通过增加直轴去磁电流,使电机的合成磁链减小,进而扩展电机的升速范围以继续提速。
电机转子一旦旋转,永磁体和定子绕组线圈就有相对运动,就会切割绕组线圈产生电流,进而产生电动势,但是这个方向和外部电源的方向是相反的,我们叫反(向)电动势(BEMF)。反电动势会抵消掉我们输入的电源电压,且反电动势与转速成正比,随着速度的上升,反电动势也会越来越大,当达到额定转速时反电动势也趋于饱和(见前文额定转速定义)。如果这时继续提速,感应电动势和电源电压之间的压差无限接近0,这意味着完全失去电流控制。如果想要继续提高速度,只能提高输入电压或者减小这个反电动势。这看起来似乎都是不可能的,输入电压受逆变器限制,对于一个给定的系统来说最大值就固定了,不可能继续增加。那只能减小反电动势了。这似乎更不可能,因为刚说反电动势与速度成正比,现在我们要通过降低反电动势来提高速度,彻底的矛盾了。虽然速度越快反电动势越大,但反电动势不是受速度唯一控制的。既然输入电压被反电动势抵消掉了,那我们是否也可以加一个电压将反电动势抵消掉。但这个电压无法从外界获取,只能想法从内部移点来,是不是越说越离谱了,从内部移点来后岂不是别人又少了,也会影响速度?如果你有这个想法说明你把力矩的作用没理解透。前文提过,零直轴电流控制方法id为0,我们现在将q轴上的电流拿点来给d轴,d轴的电流负责去抵消反电动势,的确q轴电流会减小(受总电流大小限制)进而力矩会减小,但是力矩减小不等于速度减小,力矩反应的是加速度而不是速度。
总结一下,电机正常运行过程中,d轴电流大部分时候为0(除启动阶段)。进入弱磁区域后(见下图),我们通过在d轴中注入一个反向电流,反相电流会产生磁场,叠加后会削弱定子绕组的磁通来抵消反电动势,从而达到提速的目的。
实际上前文提及过,由于定子绕组线圈之间不是正交的,当三相交流电输入后,各相线圈之间也有互感,也会产生电动势,但因为这部分比较小,为了简化分析,我们将其忽略。通常情况下我们说反电动势单纯指永磁体旋转切割定子绕组线圈产生的电动势。
虽然我很讨厌公式,但有时候还是公式看起来简洁点,上面说了那么多,其实我们可以归结到下面的公式:
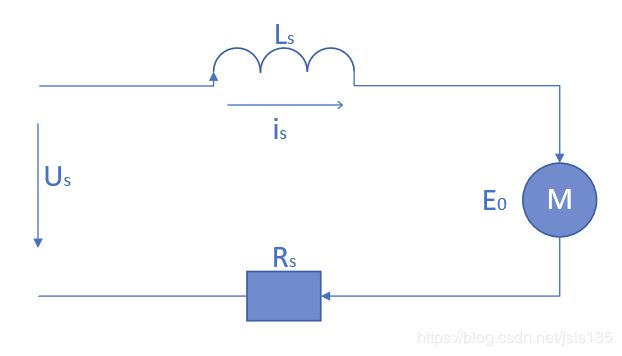
U s = R s i s + L s d i s d t + j ω s ψ f U_s=R_si_s +L_s\frac{di_s}{d_t}+j\omega_s\psi_f Us=Rsis+Lsdtdis+jωsψf
是不是看起来漂亮多了?上面这个公式是根据下图,电机的等效电路而来:
等式左边的Us受逆变器限制,最大值是固定的;这样等式右边前两部分也是不变的,那现在我们想要提速,也就是等式右边最后那部分的ωs变大,那只有ψs减小才行。这就是弱磁原理。
什么时候开始弱磁呢?
其实前面已经提过,那就是以额定速度为界,额定速度将电机整个运行速度分为两个区域:恒转矩区域和恒功率区域,如下图所示。
3.4.2 恒转矩及恒功率区域
恒转矩区域保持最大转矩以提供最大加速度来保证电机在最短时间内达到目标速度。你可能会问,如果不用最大转矩可以么?理论上来说肯定可以的,只是说这样电机性能降低了,没有发挥其最大能力。这里有一点可能容易理解错误,最大转矩有两层含义。一个是力最大,一个是力臂最大。力最大代表着电流最大,力臂最大代表力的作用方向垂直于力臂。我们这里说的是第二个力臂最大。这也是d轴电流为0的原因,如果d轴电流不为0,那么d轴和q轴上的电流合成矢量不是垂直的。而力/电流的大小由算法根据实际需要抽取。通常情况下,我们说的恒转矩区域指进入闭环后,也就是说不是真正从速度为0开始。进入闭环前一般还有开环阶段,也就是电机启动过程。
但弱磁区域为何是恒功率呢?我们再来回顾一下前文的公式:P=T*ω。在弱磁前的恒转矩区域,公式里面的T保持最大,速度ω从0开始快速上升,功率P也上升,当速度达到额定速度时,功率也达到额定功率,现在我们还想继续提高速度,这样公式就不成立啦,不守恒了。我们必须降低转矩T或者提高功率P。有一点你肯定清楚,提高功率P肯定不可能了,因为这样电机就会发热,然后被烧掉。所有我们只能降低T,这就是为何我们说弱磁的本质是牺牲转矩来提升速度的原因。所以这个问题都不用回答啦,我们别无他选。
3.4.3 弱磁常见方法
弱磁的原理看起来比较简单,但实际实现却没那么容易,各厂家的实现方式也不相同,有些方法已经有专利保护。这里列举几种常见的办法。
方法一:查表法
优点:
- 易于实现。
缺点:
- 仅适用于比较小的速度范围。
- 不能充分利用驱动能力,必须有较大的安全冗余度(比如需要考虑最大负载条件,不同电机参数的不同等)。
- 如果考虑负载,这个表是一个二维的,获取/制作这个表数据的工作量也比较大。
- 高度依赖电机参数,不同电机之间很难移植,需要重新制作表数据。
方法二:基于FOC电压限幅法
优点:
- 易于实现。
- 不依赖于电机参数,闭环系统具有反馈能力。
缺点:
- 降低最大电压能力,从而限制了最大速度范围。
- 需要正确调制电流控制器,在进入弱磁前,必须进行监管。
- 不包含扭矩最大优化控制,所以id必须限制,id限制不正确会导致失速。
方法三:负id补偿法
优点:
- 易于实现。
- 不依赖于电机参数。
- 任何时候都能保证电流调节器的调节作用,平滑快速的进入退出弱磁状态。
缺点:
- 随着转速上升,稳定性变差,不适合深度弱磁。
方法四:基于FOC调节误差法
优点:
- 在速度范围和负载扭矩方面充分利用驱动能力。
- 不依赖于电机参数,具有反馈回路,包含扭矩最大优化控制。
缺点:
- 实现非常复杂。
- 需要正确调谐的电流控制器,在弱磁控制前必须对电流进行调节。
3.4.4 最大弱磁速度
前面已经简单介绍了实现弱磁的常见方法,每种方法各有优劣,我们发现不同方法的弱磁速度范围也不相同。有些方法可以通过理论计算,而有些方法很难准确得到(可能与电机特性、负载有关)。所以最大弱磁速度很难用一个标准化的值来回答。但我们也可以根据其原理来笼统的描述:电机的最大弱磁速度不会大于电机电流以额定电流且空载运行时的最大速度。所以可以通过空载实验进行测试。
其实不难理解,以零直轴电流控制法为例,我们想想,当进入弱磁区域后,id,iq都有值,但他们的作用却不一样。前面讲原理部分已经讲过id是为了抵消反电动势,而iq和前面恒转矩区域一样,还是提供力矩的。我们换个角度描述一下。id是用来维持速度的,iq是用来抵消负载的。也就是说iq产生的力矩必须大于等于负载的力矩,否则就拉不动啦。按照这个思路,用极限的思维来考虑,如果负载为0,那iq需要的为0,全部电流给id,这时候速度是最快的。其他控制方法一样,因为最大电流代表逆变器所能提供的最大能量,有负载的情况下,速度肯定只能减小。
3.4.5 弱磁适用场景
我们知道,弱磁的目的是为了提高电机转速,但是需要明确的是不是所有需要提速的场景都可以使用弱磁。因为弱磁提速实际上是牺牲了力矩来达到目的的。了解了这个本质后,你应该很清楚弱磁适用于什么场景,那就是电机负载转矩必须随着(弱磁)速度的升高反比下降,否则就不适合使用弱磁进行提速。提速的方法也很多,比如通过机械齿轮传动比等。
3.4.6 是否可以弱磁
除了对应用场景有要求外,也不是所有电机都适合进行弱磁,这与电机结构及永磁体材料有很大关系,通常来说,表贴式/隐极式的弱磁效果没有凸极式的效果好。为什么隐极式的就不适合呢?
我们得先看看电机得电磁转矩公式:
T e = 3 2 p n [ φ f i q + ( L d − L q ) i d i q ] T_e=\frac{3}{2}p_n[\varphi_fi_q+(L_d-L_q)i_di_q] Te=23pn[φfiq+(Ld−Lq)idiq]
上式中pn是极对数,φf是磁链,方括号中第一部分代表永磁转矩,第二部分代表磁阻转矩。
由于隐极式电机 L d ≈ L q L_d\approx L_q Ld≈Lq ,由上式可知,磁阻转矩约等于0。所以不管id给多大,没有作用。这也是为什么表贴式电机很多都是采用id=0的方式(零直轴电流控制()进行控制。因为反正都等于0了,那索性电流也保持为0,这样控制起来就简单很多了。这也就是很多资料给出的公式是: T e = 3 2 ⋅ p n ⋅ φ f ⋅ i q T_e=\frac{3}{2}\cdot p_n\cdot\varphi_f\cdot i_q Te=23⋅pn⋅φf⋅iq,只包含上式中第一部分。
也有一些虽然Ld,Lq的值虽然相差比较大,也采用零直轴电流控制方法,主要目的就是为了简单,方便工程实施。但这种方法也有弊端,电流利用率不高,系统效率降低(因为我们活生生的把第二部分不为0的项弄成0了,转矩减小了)。换句话说就是相同转矩情况下,电流不是最小的。为了探索电流最优利用率,由此又产生了其他控制方法,如最大转矩电流比(MTPA: Maximum Torque Per Ampere)。
至于这个电磁转矩公式怎么来的,我还没来得及研究。
3.4.7 直轴反电动势
反电动势的概念及产生原因前面章节已经介绍过。弱磁中我们为何是在d(直)轴上加电流呢?反电动势是不是无处不在?
这个问题我们又得回顾一下dq坐标,坐标变换的目的是简化问题,方便分析。我们以最简单的一对极系统来分析,由于αβ坐标是静止的,我们也只能讨论转子的静止状态,那就是初始位置,为了获得最大力矩,通常情况下,我们定义,转子磁极初始位置保持水平,αβ坐标的α轴也水平与磁极重合,β轴与α轴正交。而dq坐标是将αβ坐标旋转起来,旋转的主要目的是将交流控制转换为直流控制。在dq坐标系下,我们的被控对象就变为直流电机一样简单了,直接控制电流大小即可。dq坐标旋转的速度与转子速度保持一致(如果是多对极,有一个极对数的倍数关系,电子转速和机械转速的区别)这样dq坐标和磁极保持相对静止。这样我们应该就比较清楚了,由于d轴与磁极平行,磁极产生的磁场无法切割d轴线圈,所以没有反电动势,这种情况下,只有q轴有反电动势,且是最大的(因为正交)。同样,我们在d轴加反向电流也是去抵消q轴线圈的磁通及反电动势。前面说过,弱磁过程中,通常情况下我们在d轴加反向电流的同时,由于受总电流大小限制,q轴电流也会跟着下降,其实q轴电流下降也会同时降低反电动势的产生。
上面只是理论上的分析,实际控制过程中,d轴也很难和磁极完全重合,会有一定相位差,或者受电机结构影响(绕组不可能那么规整),d轴是会有反电动势的,只是这部分比较小,我们可将其忽略。所以前面说了一个条件,那就是最大力矩时或者说条件就是两者没有相位差。比如在开环启动阶段,通常情况下,d轴和磁极相位差比较大,这时d轴上的反电动势也比较大。有些初始位置检测算法也需要在dq轴中交替注入电流,这时,合矢量肯定会有相位差。但因为正好弱磁区域前的状态正好时最大力矩区域,所以可以按照上述来理解。
3.4.8 反电动势作用
根据前面的介绍来看,似乎反电动势毫无用处,反而给我们带来了很多麻烦。实际上反电动势的存在也可以帮助我们解决一些问题的。比如位置观测器,在观测器中就需要使用反电动势来帮助我们确定转子的位置信息。电机启动过程(开环)有很多方法,在一些方法中还需要快速建立反电动势好建立观测器。
还有一个最典型的应用,那就是发电机,发电机正是利用了反电动势来向外界供电,只是发电机的目的和我们相反,它是尽量让反电动势越大越好。
3.5 初始位置检测(IPD)
待续。。。
3.6 位置检测—观测器
待续。。。
3.7 堵转检测
待续。。。
4. 常见问题
4.1 PWM要求
前面我们提到,通常需要专门的驱动电路,以三相系统为例,需要6个开关器件组成一个全桥电路进行控制。为了保护驱动电路,我们必须保证同一项的上桥臂和下桥臂的两个MOSFET不能同时导通,否则就短路了。所以这就对PWM提出了要求,PWM输出一共有6路(3(项)*2(上/下桥臂)=6),我们只拿其中一项来进行讨论,另外两项是一样的。
理论上如果我们将其中一路PWM取反(反相)后再输出,这样互补的两路PWM可以保证不会短路,但实际工程中,我们还要考虑到开关器件的物理特性,开/关也是需要时间的,所以我们还需要加上额外的延时,我们叫死区时间。如下图所示,下图左侧为两路互补输出,右侧为加上死区时间的波形:
有些驱动芯片带有自动反相及加死区时间的功能。但如果没有这些功能,就需要软件来实现。这种情况下就需要对它的工作原理非常清楚。
4.1.1 计算占空比的时候是否要包含死区时间?
前面我们了解到死区时间的原因是考虑开关器件的物理特性。如果我们计算占空比的时候将这个时间包含在内,那如果设置满占空比或零占空比的时候是不是就没办法保证这个最小延时了,所以很明显死区时间是不能包含在占空比里面的。只能先计算出有效占空比时间再加上这个死区时间,PWM的安全电平必须保持这两个时间之和这么久才能翻转电平。
4.1.2 死区时间怎么个加法?
这个时间是两个通道都加呢,还是在一个通道上加就行了?两个通道都加的话,是每个通道都加设置的相同死区时间还是将这个死区时间平分分别加在两个通道上?有这些疑问的人主要是因为没有明白死区的本质问题,单纯去对比没加死区和加了死区的两个波形。加死区时间的规则是:两路肯定都需要加,如果安全电平是低,则加在每个波形的下降沿;如果安全电平是高,则加在上升沿。这里的安全电平指让开关管断开时的电平。
4.1.3 会不会出现一路为低(高)电平,另一路有一个很窄的脉冲?
其实问这个问题的原因和问题2一样,还是没明白原理,单纯去看波形,因为加上死区时间的波形其中一路的脉宽大于另外一路,看起来是其中一路将另外一路包裹起来了,然后按照极限的思路去想,如果被包裹的一路的脉冲为0了,是不是另外一路还会有个脉冲,这个脉冲宽度为死区时间宽度?如果你弄明白了前面两个问题,这个问题就很容易解答了。首先如果加上死区时间,不会出现这种一直为高电平或低电平的波形,或者我们从电机控制的角度来考虑,一直为高或低说明这一项一直没变化,那电机这3相是不是转不起来了?这3相必须按照一定频率进行切换。或者你非要说我其中一路就是输出高电平或低电平(因为我是软件实现,想怎么输出就怎么输出),那你另外一路肯定也是相反的一个电平,首先必须满足互补,不应该出现一个脉冲。或者我们站在PWM模块寄存器的角度来考虑这个问题,问题一已经说了这个时间的计算方法,先计算占空比的时间,假如满占空比100%,计算出来的值等于mod寄存器值,在加上死区时间的值,那肯定是大于mod寄存器值了,反转电平的阈值比mod还大,那是不是整个周期内都不会翻转了,一直保持一个电平。
或许你看了下面标注好的图后就这些问题了,图中阴影部分为插入的死区时间(安全电平为高)。