梯度下降法求解线性回归之python实现

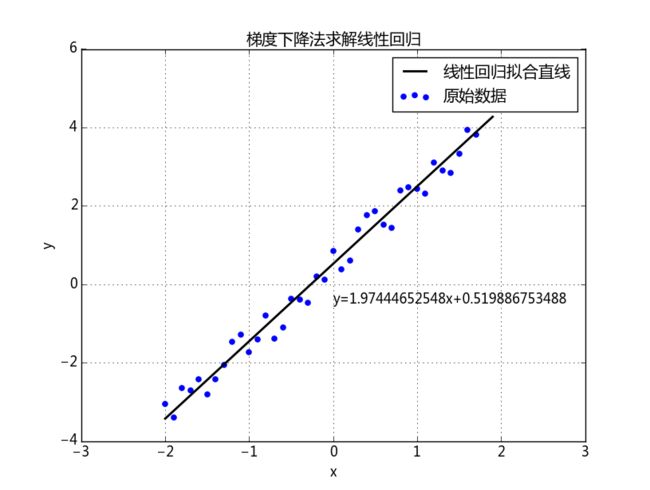
线性回归其实就是寻找一条直线拟合数据点，使得损失函数最小。直线的表达式为：

yi=ω1xi,1+ω2xi,2+ωjxi,j+...+b

损失函数的表达式为：

J=12∑i=0m(yi−ypredict_i)2

其中m为数据点总数。
现在我们使用梯度下降法求解函数 J 的最小值，梯度下降法原理示意图如下：

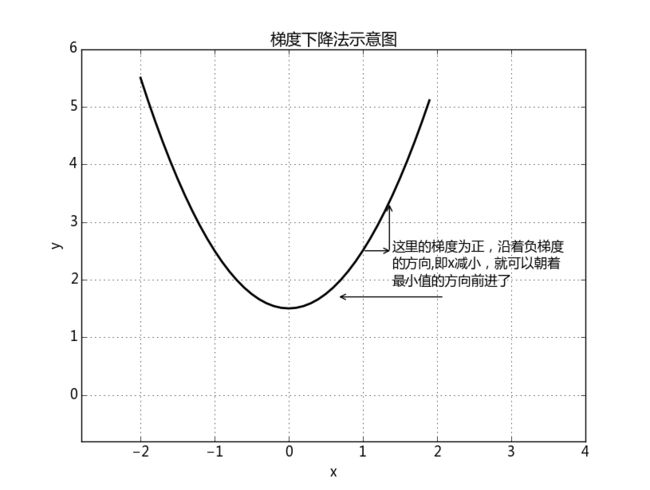
如上图所示，只要自变量 x 沿着负梯度的方向变化，就可以到达函数的最小值了，反之，如果沿着正梯度方向变化，就可以到达函数的最大值。
我们要求解 J 函数的最小值，那么就要求出每个 ω 的梯度和 b 的梯度，由于梯度太大，可能会导致自变量沿着负梯度方向变化时， J 的值出现震荡，而不是一直变小，所以在梯度的前面乘上一个很小的系数 α 。
由以上可以总结出 ω 和 b 的更新公式：

ωj=ωj−α∇J(ωj)

b=b−α∇J(b)

梯度公式（其实就是求导而已）：

∇J(ωj)=∂J∂ωj=∑i=0m(yi−ypredict_i)(−xi,j)=∑i=0m(ypredict_i−yi)xi,j

∇J(b)=∂J∂b=∑i=0m(ypredict_i−yi)

系数 α 如果随着迭代的进行越来越小的话，有利于防止迭代后期震荡的发生，是算法收敛， α 的更新公式：

α=1i+1+0.001

其中i是迭代次数，起始为0
下面为使用python具体实现梯度下降法求解线性回归
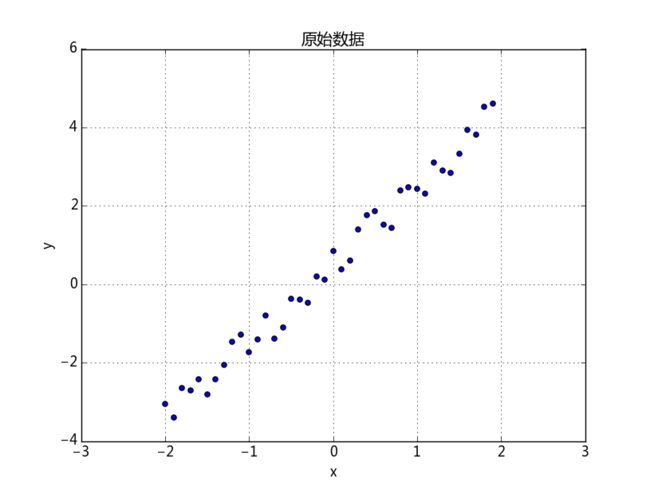
原始数据：

x = np.arange(-2,2,0.1)
y = 2*x+np.random.random(len(x))
x = x.reshape((len(x),1))
y = y.reshape((len(x),1))

开始迭代：

for i in range(maxgen):
    alpha = 1/float(i+1)+alpha0
    e = np.dot(x,seta.reshape((len(seta),1)))+b-y # 二维列向量
    mse = np.linalg.norm(e)
    delta_seta = np.dot(e.T,x)[0]
    delta_seta_norm = np.linalg.norm(delta_seta)
    b = b-alpha*np.sum(e)
    seta = seta-alpha*delta_seta
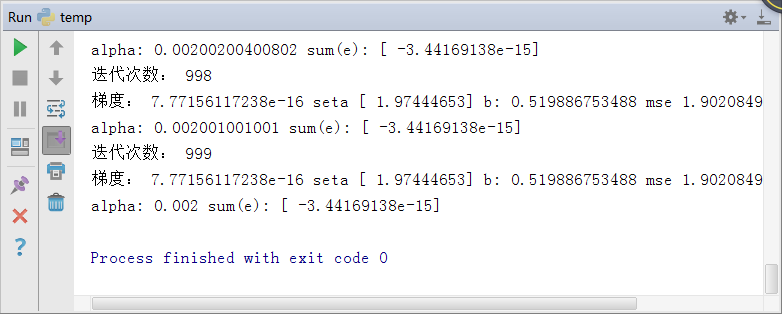
    print u'迭代次数：',i
    print u'梯度：',delta_seta_norm,'seta',seta,'b:',b,'mse',mse
    print 'alpha:',alpha,'sum(e):',sum(e)

算法运行结果：

---

如上图所示，最后梯度的值逐渐降为0，说明达到的 J 的极值点。