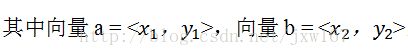3D游戏引擎系列三
笔者介绍：姜雪伟，IT公司技术合伙人，IT高级讲师，CSDN社区专家，特邀编辑，畅销书作者，国家专利发明人;已出版书籍：《手把手教你架构3D游戏引擎》电子工业出版社和《Unity3D实战核心技术详解》电子工业出版社等。
CSDN课程视频网址：http://edu.csdn.net/lecturer/144
笔者以前在游戏论坛担任过技术版主，以及在51CTO教育网，CSDN教育网，泰课在线等教育网站担任过高级讲师，跟学员或者网友经常讨论技术问题，很多人向我请教向量和矩阵在游戏开发中如何解决实际问题，为此我单独做了一些关于3D数学知识的课程讲座：《3D游戏开发基础知识》，《3D数学在Unity中的运用》、以及《3D游戏引擎架构与设计》等视频课程的讲解。旨在帮助刚接触游戏行业以及对游戏开发刚入门的初级人员，其实这些知识在大学里面已经学过了，现在参加工作了，要将所学知识运用到实践开发中。不论是3D引擎开发还是游戏逻辑开发都离不开数学理论知识的支撑，单纯的数学理论知识是非常枯燥的，从本章开始将数学知识与游戏开发的实际案例结合起来讲解。将游戏中常用的向量，矩阵，四元数以及齐次坐标等一一给大家介绍，希望对大家有所帮助，接下来先从向量开始。
向量是所有3D引擎算法的基础，因此对游戏程序员来说掌握向量的运算非常重要，向量的基本运算包括向量的加法，减法，点乘，叉乘，向量单位化等。向量是由多个分量组成，根据分量个数的多少，分为2D向量，3D向量，4D向量等。向量表示的是一条有向线段，是从一个点到另一个点的有向线段，定义的向量总是相对于原点的，而且向量是有方向和长度的。在2D游戏和3D游戏中定义的点分别是用两个量和三个量表示的，顶点与向量有何区别？单从外形上看二者是一样的，顶点和向量的区别会在后面的齐次坐标里面给大家详细的讲解。接下来介绍向量的表达式：2D向量指的是由两个参数组成，表达式为u=
在坐标轴中有两个向量a，b，
，二者是有方向的。
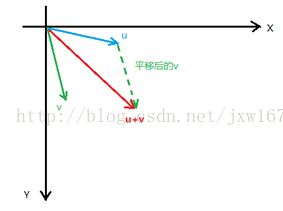
向量加法指的是两个向量的分量对应相加，简单的说两个向量相加的和就是以两个向量的边作为平行四边形长边的对角线表示，向量加法的表达式：
，在坐标系的表示如图：
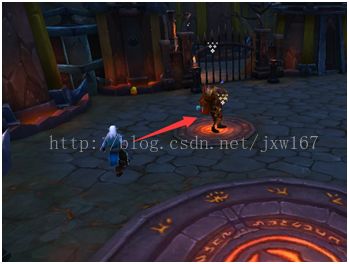
对角线长的表示两个向量相加，知道了向量相加的公式，接下来看看它在游戏编程中经常用在哪里？或者说在游戏里面是如何运用的呢？看图2-3所示，图中有两个对象：一个是玩家，另一个是怪物，假设玩家具有自动寻找目标攻击技能，玩家是如何做到自动去攻击怪物呢？已知玩家在3D场景的坐标 
，怪物在3D场景中的坐标是 
。为了让玩家能自动寻找到怪物，第一步要确定玩家追击的方向，这个方向如图：
所绘的从玩家指向怪物的箭头，用公式表示为：
，计算的结果是玩家追击怪物方向的单位化，方向是没有大小的，故进行单位化操作。取得玩家移动的方向后，接下来要计算玩家移动到靠近怪物的位置去攻击，这要用到向量的加法运算，玩家移动到怪物的位置是根据时间移动的，所以要在游戏运行的每一帧里面去调用，算式表达式：
；这样玩家就会朝着敌人追击过去，当然在玩家移动的过程中可以加入玩家动作。还可以在移动算式前加个判定二者距离远近的表达式，计算玩家移动到距离怪物多远处停止，避免二者重叠在一起。这样利用两个向量的加法运算实现了玩家移动，是不是非常简单？
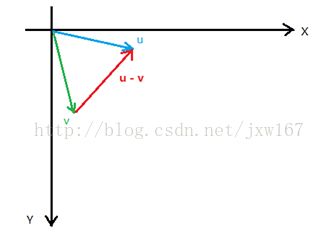
向量减法与加法正好相反，对应的是两个向量之间的各个分量相减，向量减法公式表示为：
。如图坐标系所示：
对角线短的表示两个向量相减，向量减法是与向量单位化和平方根紧密相关的。向量减法主要应用在两个方面：其一、减法可用于方向的计算，其二、减法也用于判断两个物体之间的距离。向量减法在游戏中的应用是非常广泛的，游戏中物体向另一个物体靠近时，首先要做的是将这个物体朝向另一个物体移动，比如在射击游戏里面，发射导弹追踪目标，由于目标是在不停的移动中，导弹必须不断的修正其朝向目标的方向。它的本质就是向量的减法计算，如图所示：
物体在下降的过程中导弹一直追踪着目标最后将其击毁。利用两个向量相减计算距离在游戏中也经常使用，比如怪物追踪玩家，在一定的距离之内它会锲而不舍，超过某个距离值，它就会放弃追踪返回出生地。距离的计算也是通过向量减法再平方根求得公式会在后面给出，在AI算法中也经常使用追踪策略，这样的案例很多在此就不一一列举了。
向量点积主要是用于角度的计算，向量的点积计算公式：u∙v = |u|∗|v|∗cos(theta)，向量u的长度乘上v的长度再乘上u与v之间夹角的余弦。它的几何意义是u的长度与v在u上的投影长度乘积，或者是b的长度与a在b上的投影长度乘积，它是一个标量，有正负之分，互相垂直的向量的内积为0。如图坐标系所示：
点乘在游戏中是如何运用的？假设在游戏中玩家看到了某个怪物在自己位置的某个方向，如果它要正视怪物需要旋转一定角度才能正面看到，那这个角度的计算要用到向量的点积。利用点乘公式：u∙v = |u|∗|v|∗cos(theta)，可以推导出cos(theta)= ，这样玩家就得到了旋转的角度，接下来只要让玩家旋转theta角度，当然为了转向平滑使用插值就可以了。
除了在游戏逻辑开发中使用，在GPU编程中也经常用到，开发卡通游戏时要对物体材质进行卡通渲染，在顶点着色器中进行漫射光计算，即计算顶点法向量N和光线法向量L的点积以确定其夹角是大于90度还是小于90度，如果夹角大于90度表示不接受光照，否则夹角小于90度接受光照，从而实现卡通渲染着色的明暗效果。卡通渲染要创建一个带强度级别的灰度纹理如图所示，以达到卡通绘画中的阴影过度效果。
下面摘取Shader代码的一部分VS代码片段用于展示向量的点乘运算：
VS_OUTPUT vs_main( VS_INPUT Input )
{
VS_OUTPUT Output;
Output.Position = mul( Input.Position, matViewProjection );
float3 posW = mul( matView, Input.Position );
float3 normalW = mul( Input.Normal, matView);
//通过光向量L与法向量N的点积，确定顶点接受的光线
float diffuse = max(0, dot(vecLightDir, normalW));
Output.Texcoord.x = diffuse;
Output.Texcoord.y = 0.0f;
return( Output );
}
下面语句是计算顶点接受光线函数：
float diffuse = max(0, dot(vecLightDir, normalW))公式中dot函数用于计算顶点法向量N和光线法向量L的值，然后将其值作为纹理坐标x的值。卡通渲染的效果如图所示：
中间亮度大的表示顶点法向量N和光线法向量L之间的角度小于90度，暗的地方表示二者角度大于90度。
向量叉积计算是直线和线段相关算法的核心部分，下面通过一个例子给大家普及一下基础算法。假设向量P = ( x1, y1 )，Q = ( x2,y2 )，则向量叉积定义为：P × Q = x1∗y2 - x2∗y1，其结果是一个标量，显然有公式 P × Q = - ( Q × P ) 和 P × ( - Q ) = - ( P × Q )。
叉积的一个非常重要性质是：通过它的叉乘符号判断两向量相互之间的顺逆时针关系：
若 P × Q > 0 , 则P在Q的顺时针方向。
若 P × Q < 0 , 则P在Q的逆时针方向。
若 P × Q = 0 , 则P与Q共线，但可能同向也可能反向。
叉乘还可以用于折线段的拐向判断：折线段的拐向判断方法直接由向量叉积的性质推出，对于有公共端点的线段p0p1和p1p2，通过计算公式：(p2 - p0) × (p1 - p0)的符号便可以确定折线段的拐向：
若(p2 - p0) × (p1 - p0) > 0，则p0p1在p1点拐向右侧后得到p1p2。
若(p2 - p0) × (p1 - p0) < 0，则p0p1在p1点拐向左侧后得到p1p2。
若(p2 - p0) × (p1 - p0) = 0，则p0、p1、p2三点共线。
它们在图中的表示：
在算法中经常需要判断是凸多边形还是凹多边形，这个也可以通过叉乘去实现。以两条边作为向量进行叉乘，如果全部大于等于零则是凸多边形，如果全为零则是所有边共线，否则小于零则是凹多边形。
用叉乘判断也可以判断点是在线的上方还是下方？
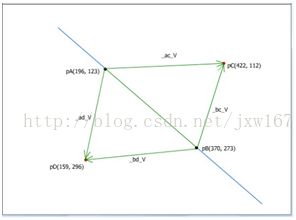
，计算这两个点在线的上方还是下方？
四个点坐标如图所示：
的向量表示为_ac_V， 
的向量表示为_bc_V， 
的向量表示为_ad_V， 
的向量表示为_bd_V。用向量的差乘计算公式：如果_ad_V×_bd_V二者的叉乘计算结果大于零表示点在 
直线的下方， 如果_ac_V ×_bc_V二者的叉乘所计算结果小于零是在直线的上方。以上计算公式可以运用到游戏中的AI算法里，在游戏中向量的叉乘主要用于判断玩家和怪物方位关系，以及具体到可以判断玩家是向左转还是向右转朝向敌人。
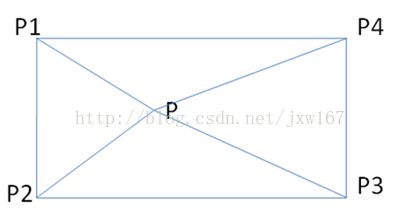
为了能让读者理解向量的叉乘，在此多举了几个例子，也为了能让读者在此基础上举一反三，同时说明向量的叉乘应用是非常广泛的，所以必须要重点掌握。本书对于重点的章节介绍的案例比较多，对于应用少的知识点一笔带过，本书还是以实用为主。
向量的长度计算公式是：
，在网络游戏中经常计算向量之间的距离，游戏中为了增加可玩性需要给怪物一定的AI功能，比如魔兽世界中的怪物追踪算法是计算怪物跟出生地距离超过一定数值它就会返回，还有射击游戏中枪支也会根据距离去使用，比如手枪射击的距离比较短，狙击枪射击的距离比较远，这些都会用到向量距离的计算。
在上几节向量运算中都使用过归一化计算公式，归一化计算方式是把向量的各个分量除以二者的长度，归一化公式：v = u / |u|，|u|表示向量长度。长度的计算前面已经讲过了，u表示向量，归一化向量主要是运用在方向的计算上，它与大小没有关系。在游戏里向量归一化主要运用于方向上的计算，比如怪物追踪玩家的方向，在前面中已经讲过，在这里就不重复了。
向量的计算在游戏中应用还是非常广泛的。关于向量的基本运算：点乘，叉乘，单位化在游戏中使用的最多。如果读者对这部分知识还不是很清楚，建议去学习一下《线性代数》，把基础夯实。本章的主要目是教读者把所学的知识灵活的运用到游戏开发中去，真正的做到学以致用，当然在此基础上读者还可以进一步的去拓展。本章讲述的向量运算在游戏中的运用相对来说比较初级，对于向量的复杂运算是把向量的各个运算公式综合运用到程序开发中。关于向量的运算全部讲完了，从下节开始讲述关于矩阵的运算。