【基础】Union-Find案例
数据结构和算法是程序员的基本功,拿健身者的话来说,这才是硬核。本系列文章主要是对该阶段的算法学习做一点记录,学习教材是广受程序员赞誉的Algorithms Fourth Edition(算法第四版)。本次学习中我将结合本书提供的两个优质资源:①配套视频:https://www.coursera.org/learn/algorithms-part1 ②配套资料:https://algs4.cs.princeton.edu/home/。加油干!(所有例子均是Java语言实现)
文章目录
- 问题引出
- 解决问题
- 算法框架准备
- 1. quick-find算法
- 2. quick-union算法
- 3. 加权重的quick-union算法
- 4. 路径压缩的加权quick-union算法
问题引出
本次要解决的问题是动态连通性问题,我将通俗的描述这个问题:任意的输入N个整数对,一个整数对就是一个元组。要求判断:输入的这个元组是否连通?
什么是连通与不连通?
如下图中的(4, 7)、(8, 9),其中比较特殊的是1,2,5,6,可以认为它们都是相互连通的。但是像(1, 4)、(5, 8)等元组因为没有一条连接线将他们连起来,所以他们是不连通的。
通过上面的描述我们可以得到几个关系:
- 自反性:假设任意两个元素(p和q)是连通的,那么p和q相连
- 对称性:如果p和q是相连的,那么q和p也是相连的
- 传递性:如果p和q相连且q和r也相连,那么p和r相连
下面将通过几种算法去解决这个问题。
解决问题
算法框架准备
所有后面的算法将基于以下的框架,某些改进只会变动如下代码的部分,将会给出说明,其他部分都是下面的代码:
public class UF {
private int[] id; // 分量id(以触点作为索引)
private int count; // 分量数量
/**
* 初始化N个触点
* 保存连通量的索引
* @param N
*/
public UF1(int N) {
// 初始化分量id数组
count = N; // 初始时刻连通分量数为N
id = new int[N];
for (int i = 0; i < N; i++) {
id[i] = i;
}
}
/**
* 连通分量的数量
*
* @return
*/
public int count() {
return count;
}
/**
* 如果p和q存在于同一个连通分量则返回true
*
* @param p
* @param q
* @return
*/
public boolean connected(int p, int q) {
return find(p) == find(q);
}
private int find(int p) {}
public void union(int p, int q) {}
public static void main(String[] args) {
int N = StdIn.readInt();
UF1 uf1 = new UF1(N);
while (!StdIn.isEmpty()) {
// 读取整数对
int p = StdIn.readInt();
int q = StdIn.readInt();
// 如果已经连通则忽略
if (uf1.connected(p, q)) continue;
// 归并分量
uf1.union(p, q);
StdOut.println(p + " " + q);
}
StdOut.println(uf1.count() + "components");
}
}
其实观察上面的代码我们发现,该算法的主要逻辑是在find()函数和union函数,大部分改变也只是这两个函数,所以优化与改进主要针对是这两个函数,下面我们正式看核心算法实现。
1. quick-find算法
算法实现如下:
/**
* p所在分量的标识符
*
* @param p
* @return
*/
private int find(int p) {
return id[p];
}
/**
* 在p和q之间添加一条连接
*
* @param p
* @param q
*/
public void union(int p, int q) {
// 将p和q归并到相同的分量中
int pID = find(p);
int qID = find(q);
// 如果p和q已经在相同的分量之中则不需要采取任何行动
if (pID == qID) return;
// 将p的分量重命名为q的名称
// 遍历整个数组,如果值id[i]==id[p] 则 id[i] = id[p] 说明两个触点连通
for (int i = 0; i < id.length; i++) {
if (id[i] == pID)
id[i] = qID;
}
count--; // 连通分量数减1
}
算法逻辑分析: 我们首先看它的构造函数:在构造函数中初始化了一个长度为N的数组,并用循环将数组赋值为 0 ~ N -1,也就是说数组的下标与数组存放的值是相等的(记住这是一个重要的点,下面会用到这个条件)。find(int) 函数的作用就是查询并返回给定数组下标的值。重点看union(),在union()函数中,我们首先通过find(int)函数查询到p和q在数组中对应的值,如果这两个值相等,说明它们是连通的,则返回true;如果不相等,那么就需要将这两个值进行连接,这里会使用到一个循环,遍历数组中的值,假如有和id[p]相等的值,就将那个值赋值为id[q],意味着这个值也与p和q连通了。其实从这里我们就可以很明显的得出:数组id[]中存放的相当于是值与值之间连通的一个索引,只有索引相同,那么它们之间才是连通的。
算法效率分析
- 构造函数:N
- find():1;操作很迅速,因为只需要访问数组一次
- union():N;操作对于每一对输入都需要遍历一次数组,代价很大
- 时间复杂度:(N+3)(N-1) ~ N^2
- 结论:quick-find 是平法级别的,不适合于处理大型问题
2. quick-union算法
quick-find 算法的效率是平方级别的,显然这样的算法是无法用于处理大型问题的。下面是改进后的quick-union算法,算法实现如下:
/**
* 通过回溯的方式找到根节点
* @param p
* @return
*/
private int find(int p) {
// 找出分量的名称
while (p != id[p]) p = id[p];
return p;
}
/**
* 在p和q之间添加一条连接
*
* @param p
* @param q
*/
public void union(int p, int q) {
// 将p和q的根节点统一
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) return;
id[pRoot] = qRoot;
count--;
}
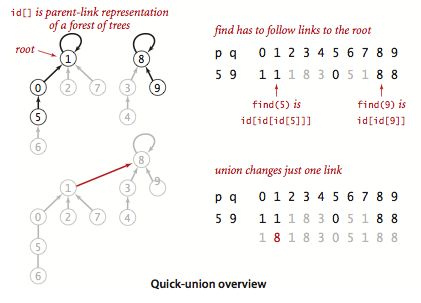
算法思想: 该算法的思想是使用森林去存储节点,然后连通性问题就变成了找两个节点是否具有共同的父节点,如果是说明两个节点是连通的。下图表示的就是这个算法思想:
图片来源:https://algs4.cs.princeton.edu/15uf/
算法逻辑分析: 通过代码我们发现,该算法将大量的时间分配给了find(int)函数,find(int)函数会通过回溯的方式去找到根节点。而union() 算法只是进行一个简单的连接操作,没有了循环。特别提一下,在本算法中,id[]存储的是节点本身或是父节点的链接。
算法效率分析
由于使用树结构来存储节点元素,那么我们很容易知道最佳情况下会是线性级别的(logN),但是最坏情况会达到平方级别(一个节点一层,N个节点N层的树)。
- 构造函数:N
- find():树的高度;如果调用数很长,则会达到 ~N^2
- union():树的高度
- 时间复杂度:最坏情况下会达到平方级别
- 结论:quick-union 是 quick-find 的改良,将union的时间复杂度由平方级别降到了线性级别,但是find的查找代价增大不适合于处理大型问题
显然该算法还不是最有算法。
3. 加权重的quick-union算法
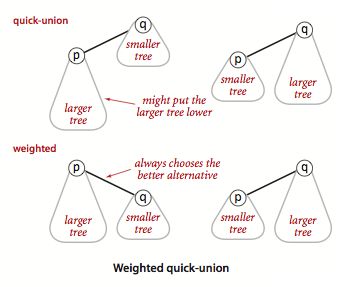
quick-union算法的严重缺陷来源于树的高度不可控,会出现极端情况,那我们是否可以想想办法对不同子树之间的合并做出调控呢?当然可以,一个非常好的方法就是为每棵子树都加上权重,这样就能很完美的解决问题,如下图所示:
图片来源:https://algs4.cs.princeton.edu/15uf/
算法实现如下:
public class WeightedQuickUnionUF {
private int[] id; // 父链接数组(触点索引构成)
// 记录每棵树的权重值
private int[] sz; // 由触点索引的各个根节点所对应的分量大小
private int count; // 连通分量数量
/**
* 初始化N个触点
* 数组中保存的是指向根节点的链接
*
* @param N
*/
public WeightedQuickUnionUF(int N) {
count = N; // 初始时刻连通分量数为N
id = new int[N];
for (int i = 0; i < N; i++) {
id[i] = i;
}
// 初始化时每个节点就是一颗单节点树,权重都是1
sz = new int[N];
for (int i = 0; i < N; i++) {
sz[i] = 1;
}
}
/**
* 连通分量的数量
*
* @return
*/
public int count() {
return count;
}
/**
* 如果p和q存在于同一个连通分量则返回true
*
* @param p
* @param q
* @return
*/
public boolean connected(int p, int q) {
return find(p) == find(q);
}
/**
* 通过回溯的方式找到根节点
*
* @param p
* @return
*/
private int find(int p) {
// 跟随链接找到根节点
while (p != id[p]) p = id[p];
return p;
}
/**
* 在p和q之间添加一条连接
*
* @param p
* @param q
*/
public void union(int p, int q) {
// 将p和q的根节点统一
int i = find(p);
int j = find(q);
if (i == j) return;
// 将小树的根节点连接到大树的根节点
if (sz[i] < sz[j]) {
id[i] = j;
sz[j] += sz[i];
} else {
id[j] = i;
sz[i] += sz[j];
}
count--;
}
public static void main(String[] args) {
int N = StdIn.readInt();
WeightedQuickUnionUF uf1 = new WeightedQuickUnionUF(N);
while (!StdIn.isEmpty()) {
// 读取整数对
int p = StdIn.readInt();
int q = StdIn.readInt();
// 如果已经连通则忽略
if (uf1.connected(p, q)) continue;
// 归并分量
uf1.union(p, q);
StdOut.println(p + " " + q);
}
StdOut.println(uf1.count() + "components");
}
}
该算法相对quick-union算法来说只是加了一个数组sz[],该数组用来跟踪记录每一棵子树的权重,保证权重小的子树会添加到权重大的下。
算法效率分析
- 构造函数:N
- find(): log2N
- union():log2N
- 时间复杂度:O(log2N),能保证对数级别的性能
- 结论:加权quick-union算法是目前处理动态连通性问题的最优算法,适合处理大型问题
4. 路径压缩的加权quick-union算法
算法实现如下:
/**
* 通过回溯的方式找到根节点
*
* @param p
* @return
*/
private int find(int p) {
// 跟随链接找到根节点
while (p != id[p]) {
id[p] = id[id[p]];
p = id[p];
}
return p;
}
我们发现该算法相对于 加权重的quick-union算法 改动只是在find()函数中,只加了一行:id[p] = id[id[p]],该行的作用就是将每棵子树直接连在另一棵大子树的根节点上,这也就是该算法的思想:既然分层越少越好,那直接就将子树连接到根节点
算法效率分析
- 构造函数:N
- find(): 均摊成本,不可控
- union():无限接近1但仍然没有达到1