自己动手写一个轻巧,高效的正则表达式引擎
http://www.graphviz.org/
原文地址:
http://swtch.com/~rsc/regexp/regexp1.html
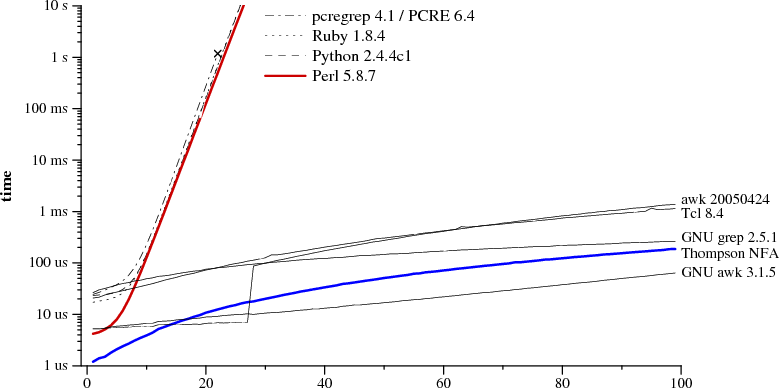
下面两张表是两种正则表达式引擎的表现。其中一种用在许多语言的标准解释器,有Perl。另外一种用在为数不多的地方,主要是awk和grep。这两种引擎有着极为不同的性能表现
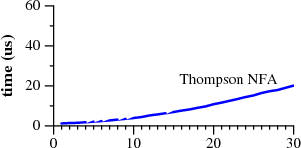
图1 a?(n)a(n)匹配a(n)用时
用(n)代表字符的重复次数,a?(3)a(3)就是a?a?a?aaa的简写。两张图代表了a?(n)a(n)匹配a(n)的用时。
注意Perl用了60多秒匹配29个字符。另外一个,Thompson NFA,只花了20微秒。Thompson NFA在29个字符的表现上比Perl快100000倍。这个趋势往后还是一样的。Thompson处理100个字符不到200毫秒,而Perl要花10e15年。(Perl只是一个典型,这张表可以换成Python,PHP,Ruby或者其他)
似乎难以置信:也许你用过Perl,似乎正则匹配实际上没有这么慢。大多情况,它在Perl这是很快的。尽管,你可以写出这种非主流的表达式,而且Perl的表现也很慢。然而,在Thompson NFA的实现中,没有这种非主流的的正则表达式。对比这两张图,产生了一个问题,为什么Perl不用Thompson NFA。本是可以用,也应该用。这是下文要说的。
历史上,正则表达式是计算科学当中理论指导实际编程的精彩案例。它原本只是被理论家发展为一种简单的计算机模型,后来被Ken Thompson介绍给了CTSS项目的QED编辑器器的开发人员。Dennis Ritchie随后在GE-TSS的QED中也引入了正则表达式。这两人税后从事Unix开发,引入了正则表达式。在70年代末,正则表达式成为了Unix平台许多工具的关键特性,像ed,sed,grep, awk,lex。
今天,正则表达式变成了,好的理论有着差的实现的典型例子。今天许多工具用到的正在表达式实现版本,比起30年前的Unix上工具用到的要慢上许多。
这篇文章涉及的理论有:正则表达式,有限自动机,正则表达式搜索算法(KenTompson在60年代中期发明)。理论也要联系实际,描述下Thompson算法的简单实现,400行不到的C代码,比起Perl当中的性能好很多。比起很多Perl,Python, PCRE等语言中的实现要好很多。最后讨论一下理论是如何被转化为实现的。
正则表达式
正则表达式描述字符的集合。当某个字符串在这个集合中,就达成了匹配。最简单的正则表达式是一个文字字母。除了元字符 *+()| 以外,字符匹配自身。要匹配一个元字符,在前面加上反斜杠:\+ 匹配文字+字符。
两个表达式可以并行或串行连接成为一个新的表达式:如果e1匹配s,e2匹配t,那么e1|e2匹配s或者t,e1e2匹配st。
元字符 *,+,?是重复运算符:e*匹配的是0个或多个可以不同的字符串,每个字符串和e匹配;e+匹配一次或多次;e?匹配0次或1次。
运算符的优先级,从最低到最高,首先是并行符,然后是串行符,最后是重复符号。括号和算术表达式中一样可是改变结合性。就像是这样:ab|cd等同于(ab)|(cd);ab*等同a(b*)。
现在为止描述的语法只是传统Unix egrep正则表达式语法的子集。这个子集足以描述所有的正则语言:宽泛地说,正则语言是:在使用有限的内存下,遍历一次就能匹配的字符的集合。新的的正则表达式设施,像Perl当中,已经添加了许多新的运算符和专业序列。这些扩充使其更加简洁,因为使用传统的语法要更长一些。但有时显得得隐晦,甚至常常不是那么有用。
正则表达式当中一项常用而有用的扩展是后向引用。\1和\2这样的后向引用,匹配前面带有括号的表达式匹配过的字符,(cat|dog)\1匹配 catcat和dogdog,而不是catdog,dogcat。从理论上来说,带有后向引用的正则表达式不是正则表达式。后向引用带来了巨大的消耗:最坏情况下,已知的最佳搜索算法需要指数复杂度,和Perl一样。Perl不可能去掉后向引用的支持,但是不涉及后向引用的地方可以用高效算法。本文就是要描述高效算法。
有限自动机
另一种描述字符串集合的方式是有限自动机。有限自动机也叫状态机,下面会交替地用自动机,机器
下面是一个简单的例子,表达式a(bb)+a的状态机如何匹配字符串的:
图DFA for a(bb)+a
有限自动机总是处于某个状态,在途中用圆表示。圆中的数字是便于讨论的标记;本身不是状态机的操作。当它读取字符串时,就在转移状态。它有两个特别的状态:开始状态s0和匹配状态s4。开始状态由单箭头指向,匹配状态是两个圆。
状态机一次读取一个输入字符,随着输入的箭头转移状态。如果输入是abbbba。状态读取第一个字符,a,它在开始状态s0。跟着一个箭头到状态是s1。状态机读取余下的字符串继续上面的过程:b到s2,b到s3,b到s2,b到s3,最后a到s4。
图DFA运行在 abbbba上
状态机在S4结束,所以匹配这个字符串。如果在一个非匹配状态结束,就没有达成匹配。如果在状态机执行的任意时刻,如果没有箭头来转移当前的字符,状态机提早结束。
我们现在考虑的状态机被称为决定性有限自动机(DFA)。因为在任何状态,每个可能的输入字符,最多只会让它转到一个新的状态。我们也可以构造有多个后续转移状态的状态机。例如,这个状态机等效于前面的的,但非决定性。
图NFA a(bb)+a
上面的状态机不是确定性的,因为在s2读到b以后,有多种选择转移到下个状态:它可以转移到s1接下来来匹配bb,或者到s3匹配最后一个a。状态机在当前状态下不能提前看剩下的字符,所以不知道哪种选择才是正确的。这种情况下状态机能否猜中就变得有趣了。这种状态机就叫做非确定性有限自动机(NFAs或者NDFAs)。如果读取的字符串可以沿着箭头到达匹配状态,NFA就实现了匹配。
有时候,使得NFA中的箭头没有相应的输入字符也是很方便的。我们试着去掉箭头上的标记。一个NFA,仍何时候都能不读取输入的情况下,沿着一个非标记的箭头走。这个NFA等价于前两个,但是未标记的箭头最清晰地展现了与a(bb)+a地联系
图未标记的NFA
把正则表达式转换为NFA
正则表达式和NFAs本质是一样的:每个正则表达式有一个等效的NFA(它们匹配同样的字符串),反之亦然。(DFAs和它们也是等效;稍后会看到。)有多种把NFA转换为NFA的方法。这里描述的方法在Thompson 1968 CACM的论文中谈到。
正则表达式的NFA由子串的局部NFA构造而成,每个操作符的构造方式是不同的。局部NFAs没有匹配状态:它们有若干悬挂箭头。构造过程就是连接箭头和匹配状态。
匹配单个字符的NFAs是这样:
![]()
e1e2的连接NFA,是把e1的最后箭头和e2的头部相连:
![]()
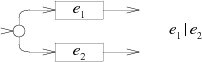
e1|e2的选择NFA,添加一个新的开始状态来二选一:
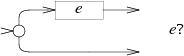
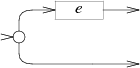
e?的NFA在e和一条空的路径间选择:
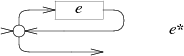
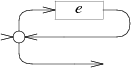
e*的NFA用了同样的选择,但是循环匹配e回到最初:
e+的NFA同样构造循环,但是至少通过e一次:
统计上面的图,正则表达式的每个字符或元字符产生了一个状态,包括括号。因此,NFA中的状态数最少是原始字符串长度。
正如上面的NFA,总是可以去掉未标记的箭头,也总是可以产生没有未标记箭头的NFA。未标记箭头的NFA便于阅读,也让C的实现简单,因而我们沿用下来。
正则表达式搜索算法
现在我们有办法测试一个正则表达式是否匹配一串字符:把正则表达式转换为一个NFA,然后把字符串作为输入来运行NFA。记住,NFA有正确猜出选择下个状态的能力:要在一台普通电脑上运行NFA ,就要找到模拟试探的方法。
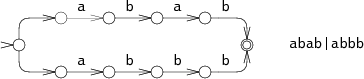
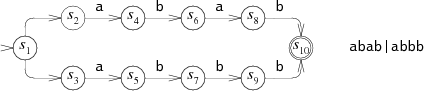
一种模拟完美猜测的方法猜一种情况,如果不可行,换另一种。例如,考虑abab|abbb的NFA跑在abbb上:
图abab|abbb的NFA
图abbb的回溯执行
在第0步,NFA必须做出选择:匹配 abab还是abbb。在图中,NFA尝试了abab,但是在第3步失败了。NFA然后尝试其他选择,到了第4步最后匹配成功。这种回溯方法有一个简单的递归实现,但是成功之前,要多次读取字符串。如果字符串是不可匹配的,状态机在失败前会走遍所有的执行路径。这个例子中NFA仅仅试了两条路径,但是最坏情况下,有可能有指数级别的路径,导致非常慢的运行时间。
更加有效但是复杂的方式是同时尝试所有选择。它让状态一次处于多个状态。处理每个字符时,它从每个状态沿着每个箭头匹配此字符。
图abbb的并行执行
状态机始于起始状态,以及所有源于始状态的没有标签箭头的状态。在步骤1和2,NFA同时在两个状态。只有在第3步,才到达单独的状态。这种多状态的方法读取字符串一次,同时探索所有路径。最坏情况下,NFA在每一步可能处于所有的状态,也因此每一步的开销和字符串的长度无关,是一个恒定的值。因此任意长度的字符串也能在线性时间处理。比起回溯算法的指数时间,这是巨大的改进。高小来源于探索可达状态的集合,而不是尝试每条路径去匹配。在一个有n个节点的NFA,每一步只有n个可达的状态,但是有可能有2的n次方条路径。
实现
Thompson在1968年的论文中介绍了多状态的算法。在他的公式里,NFA的状态的状态用短小机器码序列表示,状态的列表是一系列称为指令的函数。本质上,Thompson巧妙地把正则表达式编译为机器码。40年以后,电脑更快了,机器码的实现不是唯一。下面的部分给出一个简洁的ANSI C的实现。少于400行的源码和测试脚本在这里可以下载。不熟悉C和指针的读者可以阅读描述,忽略实际的代码
实现:编译为NFA
第一步,吧正则表达式编译为等效的NFA。在C程序中,用互相连接的状态结构体表示NFA:
struct State
{
int c;
State*out;
State*out1;
intlastlist;
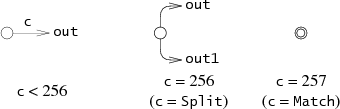
};每个状态代表三个NFA局部之一,由c值决定。Lastlist在下面会解释
图可能的NFA局部。
Thompson的论文,编译器以后缀表达式建立NFA,这些表达式加上了”.”显示地表达连接运算符。函数re2post把一个中缀的正则表达式如“a(bb)+a”转换一个等效的后缀表达式“abb.+.a”。真实的实现当中用点作为“任意字符”的元字符而不是连接符号。真实的实现也是在解析表达式中建立一个合适的NFA,而不是显式地建一个后缀表达式。然而,后缀的版本更加方便,和Thompson的论文联系得更紧密。
当编译器查看后缀表达式时,维持了NFA局部的一个栈。依次把NFA局部压入栈中,如果遇到运算符,把NFA局部弹出栈,然后压入一个新的局部。例如,编译完abb的abb.+.a,栈中包含了a,b,b的NFA局部。编译到“.”时,把两个b的局部弹出,然后压入一个bb的连接。每个NFA的局部定义为其实状态和它的转移箭头:
struct Frag
{
State *start;
Ptrlist *out;
};Start指向这个局部的开始状态,out是指针列表,指向未连接任何状态的State*指针。因此它们是悬挂指针。
一些处理指针列表的辅助函数:
Ptrlist *list1(State **outp);
Ptrlist *append(Ptrlist *l1, Ptrlist *l2);
void patch(Ptrlist *l, State *s);List1建立一个包含单个指针outp的指针列表。Append连接器两个指针列表。Patch把列表1中的悬挂指针和状态s连接起来:让列表l中的每个outp,*outp=s。
有了这些辅助函数和NFA局部的栈,编译器遍历这个后缀表达式。最后,剩下一个单独的局部,然后补上一个匹配状态就完成了NFA。
State* post2nfa(char *postfix)
{
char *p;
Frag stack[1000], *stackp, e1, e2, e;
State *s;
#define push(s) *stackp++ = s
#define pop() *--stackp
stackp = stack;
for(p=postfix; *p; p++){
switch(*p){
/* compilation cases, described below */
}
}
e = pop();
patch(e.out, matchstate);
return e.start;
}下面的编译过程模拟了上面描述的解析过程。
文字字符:
default:
s = state(*p, NULL, NULL);
push(frag(s, list1(&s->out));
break;连接符号:
![]()
case '.':
e2 = pop();
e1 = pop();
patch(e1.out, e2.start);
push(frag(e1.start, e2.out));
break;选择符号:
case '|':
e2 = pop();
e1 = pop();
s = state(Split, e1.start, e2.start);
push(frag(s, append(e1.out, e2.out)));
break;重复0次或1次符号:
case '?':
e = pop();
s = state(Split, e.start, NULL);
push(frag(s, append(e.out, list1(&s->out1))));
break;重复0次或多次:
case '*':
e = pop();
s = state(Split, e.start, NULL);
patch(e.out, s);
push(frag(s, list1(&s->out1)));
break;重复1次或多次:
case '+':
e = pop();
s = state(Split, e.start, NULL);
patch(e.out, s);
push(frag(e.start, list1(&s->out1)));
break;实现:模拟NFA
现在NFA已经建立,我们开始运行。模拟需要跟踪状态集合,它们存在一个简单的线性表当中:
struct List
{
State **s;
int n;
};模拟用两个表:clist是NFA当前的状态集合,nlist是NFA处理完当前字符下面要进入的状态集合。初始化时,clist只有开始状态,然后每次走一步。
int
match(State *start, char *s)
{
List *clist, *nlist, *t;
/* l1 and l2 are preallocated globals */
clist = startlist(start, &l1);
nlist = &l2;
for(; *s; s++){
step(clist, *s, nlist);
t = clist; clist = nlist; nlist = t; /* swap clist, nlist */
}
return ismatch(clist);
} 为了避免在每一次迭代中申请内存, match用两个预先申请的表l1和l2作为clist和nlist,每一步交换二者。
如果最后的状态列表包含匹配状态,就达成了匹配。
int
ismatch(List *l)
{
int i;
for(i=0; in; i++)
if(l->s[i] == matchstate)
return 1;
return 0;
} addstate添加一个状态到列表中,但是已经在里面了不会添加。每一次添加的时候都要遍历整个列表很低效;实际上listid作为列表的生成数。当addstate添加s,它在s->lastlist记录listid。如果两者相同,s在列表创建时已经在其中了。Addstate也接受未标记的箭头:如果s是带有两个未标记箭头,且指向新的状态的Split状态,addstate把这些状态添加到list中而不是s。
void
addstate(List *l, State *s)
{
if(s == NULL || s->lastlist == listid)
return;
s->lastlist = listid;
if(s->c == Split){
/* follow unlabeled arrows */
addstate(l, s->out);
addstate(l, s->out1);
return;
}
l->s[l->n++] = s;
} startlist通过加入开始状态创建初始列表:
List*
startlist(State *s, List *l)
{
listid++;
l->n = 0;
addstate(l, s);
return l;
} 最后,step用单个字符推进NFA,用当前列表clist计算后续列表nlist。
void
step(List *clist, int c, List *nlist)
{
int i;
State *s;
listid++;
nlist->n = 0;
for(i=0; in; i++){
s = clist->s[i];
if(s->c == c)
addstate(nlist, s->out);
}
} 性能
刚才描述的C实现没有可以追求性能。即使这样, 规模上去以后,线性算法的普通实现也可以轻松赶超指数时间算法的优化实现。用一个不合理的正则表达式测试多种流行的正则表达式引擎很好地证明这一点。
用a?(n)a(n)来说。匹配字符串a(n),a?没有匹配任何字符,整个字符串由a(n)匹配。回溯算法的正则表达式引擎处理匹配0次或1次的“?”符号时,先匹配1次,然后匹配0次。要做n次这样的选择,总共2的n次方种可能。只有最后一种可能,对于所有的“?”做0次匹配,才能匹配。回溯算法需要O(2的n次方)时间复杂度,因此不能n不能超过25。
相对来说,Thompson的算法维持长度几乎是n的状态列表,处理长度是n的字符串,总共是O(n平方)时间复杂度。(运行时间是超线性的,因为输入增加时,正则表达式不是恒定的。长度为m的正则表达式匹配长度为n的文本时,Thompson NFA需要O(mn)的复杂度。)
下面的图描绘了检查a?(n)a(n)匹配a(n)的用时:
从图中看,Perl,PCRE,Python和Ruby用的是递归回溯算法。PCRE在n=23时停止执行,因为超过最大步数后就放弃递归回溯。在Perl 5.6中,除非使用回溯算法,声称Perl的正则表达式引擎会记录下递归回溯搜索,这样耗费一定内存,避免消耗指数时间。正如性能图上显示,记忆表并不完善:Perl即使在不用回溯算法,运行时间指数增长。虽然没有测量,Java也适用回溯实现。实际上,java.util.regex接口需要回溯实现,因为任何Java代码可以被替换为匹配路径。PHP用的是PCRE库。
蓝色的粗线是C实现的Thompson算法。Awk,Tcl,GNU grep,GNU awk建立DFAs,通过预先处理或者用下面要说的飞一般的构建方法。
有人会说测试对回溯算法不公平,因为用的都是极端测试用例。这种说法忽略了:一种算法对所有的输入都有可预计,恒定,快速的运行时间;另一个平常运行很快但是在一些用例上要数年的CPU时间。是你,选哪一个?尽管这么的的差距的在实际中很少产生,但是差距依然存在。例如用(.*) (.*) (.*) (.*) (.*)来分开五个用空格隔开的部分,或是在选择符号中最常出现的分支不是排在前面。总之,程序员总是避免耗时的部分,否则就要进行优化。Thompson的NFA就不需要这样的调整:没有低效的正则表达式。
缓存NFA建立DFA
回想DFA比NFA更加高效,因为DFA同一时间只处于一个状态:它不会有多个后续状态。任何的NFA都可以转化为等效的DAF,其中DFA的各个状态对应NFA的一系列状态。
例如,abab|abbb的NFA是:
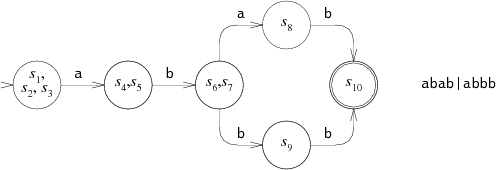
等效的DFA是:
DFA中的各个状态对应NFA的一系列状态。
某种意义上,Thompson的NFA的演算就是执行等效的DFA:各个列表对应DFA的一些状态,step函数在一个列表和后续字符下,计算下个进入的DFA状态。Thompson的算法通过重构DFA的状态模拟DFA。如果不丢掉每一步的计算,缓存列表,避免以后重复计算,只要DFA必要的计算。这节讨论这种算法的实现。从上节的NFA实现开始,我们只有添加不到100行代码完成DFA的实现。
要实现缓存,先引入一个DFA的数据类型:
struct DState
{
List l;
DState *next[256];
DState *left;
DState *right;
};DState是列表l的缓存拷贝。数组next包含了每个可能输入字符的后续状态的指针:如果当前状态是d,下面的输入字符是c,d->next[c]是后续状态。如果d->next[c]是null,后续状态就还没有算出来。NextState计算,记录,返回给定状态,字符的后续状态。
正则表达式匹配重复d->next[c],调用nextstate计算新的状态。
int
match(DState *start, char *s)
{
int c;
DState *d, *next;
d = start;
for(; *s; s++){
c = *s & 0xFF;
if((next = d->next[c]) ==NULL)
next = nextstate(d, c);
d = next;
}
return ismatch(&d->l);
}所有已经计算的DState存在一个结构体里,可以通过它的List查询DState。因此,使用二叉树的结构,用有序的List当作键值。dstate函数对给定的List返回DState,必要时做内存申请:
DState*
dstate(List *l)
{
int i;
DState **dp, *d;
static DState *alldstates;
qsort(l->s, l->n, sizeofl->s[0], ptrcmp);
/* look in tree for existingDState */
dp = &alldstates;
while((d = *dp) != NULL){
i = listcmp(l, &d->l);
if(i < 0)
dp = &d->left;
else if(i > 0)
dp = &d->right;
else
return d;
}
/* allocate, initialize newDState */
d = malloc(sizeof *d + l->n*sizeofl->s[0]);
memset(d, 0, sizeof *d);
d->l.s = (State**)(d+1);
memmove(d->l.s, l->s,l->n*sizeof l->s[0]);
d->l.n = l->n;
/* insert in tree */
*dp = d;
return d;
}nextstate运行NFA的step返回相应的DState:
DState*
nextstate(DState *d, int c)
{
step(&d->l, c, &l1);
return d->next[c] =dstate(&l1);
}最后,DFA的开始状态时DState,对应NFA的开始列表:
DState*
startdstate(State *start)
{
return dstate(startlist(start,&l1));
}(在NFA匹配时,l1时预先申请的List)
DState对应DFA的状态,但是DFA是在需要时建立:如果DFA状态在搜索时没有遇到,就不存在缓存中。选择运算符会立即计算整个DFA。如此一来,去掉了条件分支,match会快一些,但是增加了开始时间和内存使用。
这种DFA可以飞速运行了,构造时的内存使用如何呢。由于DState仅仅是step函数的缓存,如果缓存增加过快,dstate的实现可以扔掉整个DFA。这种缓存策略仅仅需要在dstate和nextstate中,添加额外的几行代码,加起来差不多50行的内存分配代码。这里有一种实现。(Awk也用了相似的大小限制的缓存策略,固定的32大小的缓存状态;这解释了上图中n=28,性能的非连续性。)
正则表达式的NFA倾向于展示好的局部特性:在多数文本上,它们总是一遍遍访问同一个状态和选择同一个转换箭头。缓存因此变得有意义:一个箭头第一次被选择了后,后续状态需要被计算出来,但是以后访问这个箭头只是内存的访问。实际基于DFA的实现可以利用其他的优化跑得更快。这篇文章的姊妹篇(还没写)要讨论基于DFA的正则表达式更多的细节。
实际世界当中的正则表达式
实际编程的正则表达式比起上面描述的实现要复杂得多。这部分简单地描述它的的基本复杂性,完整的细节超出了这篇介绍文章的范畴。if(/([0-9]+-[0-9]+-[0-9]+) ([0-9]+:[0-9]+)/){
print "date: $1, time: $2\n";
} 断言(Assertions)。传统正则表达式的元字符^和$可以视为对文本的断言:^断言前面的字符是一个换行(或者是字符串的开头),而$断言下一个字符是换行(或者字符串的结尾)。Perl添加更多的断言,像词边界\b,它断言前一个字符是字母数字但是下一个不是,反之亦然。Perl甚至泛化到任意条件,称为前向断言:(?=re)断言当前输入位置后面的文本匹配re。(?|re)是相似的但是断言文本不匹配re。后向断言 (?<=re) (?<|re)是相似的,但是对当前输入位置前面的文本做断言。像^,$和\b可以简单用到NFA中,延迟一个字节的匹配。泛化的断言较难调整,但是理论上可以用到NFA中。