Python绘制流程图

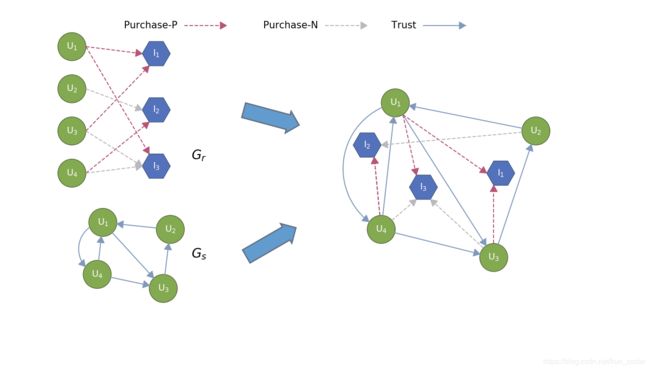
欢迎大神尝试

import matplotlib.pyplot as plt
import numpy as np
import matplotlib.patches as mpatches
plt.subplots_adjust(left=0.00, bottom=0.0, right=1.00, top=0.95, wspace=0.0, hspace=0.00)


def hexagon_with_text(ax,x,y,text,size,**kwargs):
    xy=np.array([x,y])
    hexagon = mpatches.RegularPolygon(xy, 6, radius=size,facecolor='#5472bb',edgecolor='#3f597c', orientation=np.pi / 2)
    ax.add_patch(hexagon)
    ax.text(xy[0],xy[1],text,fontsize=size*14,color='white',va='center',ha='center')

def circle_with_text(ax,x,y,text,size,**kwargs):
    xy=np.array([x,y])
    circle = mpatches.Circle(xy, radius=size,facecolor='#83aa51',edgecolor='#546538')
    ax.add_patch(circle)
    ax.text(xy[0],xy[1],text,fontsize=size*14,color='white',va='center',ha='center')

def arrow(ax,x,y,size,**kwargs):
    ax.plot(x,y,**kwargs)
    theta=np.arctan2(x[1]-x[0],y[1]-y[0])
    xy=np.array([x[1]-size*np.sin(theta),y[1]-size*np.cos(theta)])
    triangle = mpatches.RegularPolygon(xy, 3, radius=size,color=kwargs['color'], orientation=-theta)
    ax.add_patch(triangle)

def arrow_with_rad(ax,x,y,radius,size,**kwargs):
    d=np.sqrt((x[1]-x[0])**2+(y[1]-y[0])**2)

    theta=np.arctan2(x[1]-x[0],y[0]-y[1])

    x0=(x[0]+x[1])/2+np.cos(theta)*np.sqrt(radius**2-(d/2)**2)
    y0=(y[0]+y[1])/2+np.sin(theta)*np.sqrt(radius**2-(d/2)**2)

    theta1=np.arctan2(y[0]-y0,x[0]-x0)
    theta2=np.arctan2(y[1]-y0,x[1]-x0)

    arc_x = []
    arc_y = []

    for theta in np.arange(theta1,theta2+(np.pi*2),np.pi/180):
        temp_x=x0 + radius * np.cos(theta)
        temp_y=y0 + radius * np.sin(theta)
        if((temp_x-x[0])**2+(temp_y-y[0])**2>1 and (temp_x-x[1])**2+(temp_y-y[1])**2>1):
            arc_x.append(temp_x)
            arc_y.append(temp_y)
    ax.plot(arc_x,arc_y,**kwargs)

    theta=np.arctan2(arc_y[-2]-arc_y[-1],arc_x[-2]-arc_x[-1])
    xy=np.array([arc_x[-1]+size*np.cos(theta),arc_y[-1]+size*np.sin(theta)])
    triangle = mpatches.RegularPolygon(xy, 3, radius=size,color=kwargs['color'], orientation=np.pi/2+theta)
    ax.add_patch(triangle)

ax=plt.subplot(1,1,1,aspect='equal')
ax.axis('off')

circle_with_text(ax,2,23,'$\mathrm{U_{1}}$',1)
circle_with_text(ax,2,20,'$\mathrm{U_{2}}$',1)
circle_with_text(ax,2,17,'$\mathrm{U_{3}}$',1)
circle_with_text(ax,2,14,'$\mathrm{U_{4}}$',1)

hexagon_with_text(ax,8,22.5,'$\mathrm{I_{1}}$',1)
hexagon_with_text(ax,8,18.5,'$\mathrm{I_{2}}$',1)
hexagon_with_text(ax,8,14.5,'$\mathrm{I_{3}}$',1)

arrow(ax,[3,8+np.cos(np.pi*3/3)],[23,22.5+np.sin(np.pi*3/3)],0.3,color='#b65576',linestyle='--')
arrow(ax,[3,8+np.cos(np.pi*2/3)],[23,14.5+np.sin(np.pi*2/3)],0.3,color='#b65576',linestyle='--')
arrow(ax,[3,8+np.cos(np.pi*4/3)],[17,22.5+np.sin(np.pi*4/3)],0.3,color='#b65576',linestyle='--')
arrow(ax,[3,8+np.cos(np.pi*4/3)],[14,18.5+np.sin(np.pi*4/3)],0.3,color='#b65576',linestyle='--')

arrow(ax,[3,8+np.cos(np.pi*3/3)],[20,18.5+np.sin(np.pi*3/3)],0.3,color='#b9b8bd',linestyle='--')
arrow(ax,[3,8+np.cos(np.pi*3/3)],[17,14.5+np.sin(np.pi*3/3)],0.3,color='#b9b8bd',linestyle='--')
arrow(ax,[3,8+np.cos(np.pi*3/3)],[14,14.5+np.sin(np.pi*3/3)],0.3,color='#b9b8bd',linestyle='--')

ax.text(10.5,15,'${G_{r}}$',fontsize=20)

circle_with_text(ax,4.2,10.5,'$\mathrm{U_{1}}$',1)
circle_with_text(ax,9.0,10.0,'$\mathrm{U_{2}}$',1)
circle_with_text(ax,8.5,5.8,'$\mathrm{U_{3}}$',1)
circle_with_text(ax,3.8,6.8,'$\mathrm{U_{4}}$',1)

theta=-np.pi/2-np.arctan2(9.0-4.2,10.0-10.5)
arrow(ax,[9.0+np.cos(theta),4.2-np.cos(theta)],[10.0+np.sin(theta),10.5-np.sin(theta)],0.3,color='#8199bb')

theta=-np.pi/2-np.arctan2(8.5-9.0,5.8-10.0)
arrow(ax,[8.5+np.cos(theta),9.0-np.cos(theta)],[5.8+np.sin(theta),10.0-np.sin(theta)],0.3,color='#8199bb')

theta=-np.pi/2-np.arctan2(3.8-4.2,6.8-10.5)
arrow(ax,[3.8+np.cos(theta),4.2-np.cos(theta)],[6.8+np.sin(theta),10.5-np.sin(theta)],0.3,color='#8199bb')

theta=-np.pi/2-np.arctan2(3.8-8.5,6.8-5.8)
arrow(ax,[3.8+np.cos(theta),8.5-np.cos(theta)],[6.8+np.sin(theta),5.8-np.sin(theta)],0.3,color='#8199bb')

theta=-np.pi/2-np.arctan2(4.2-8.5,10.5-5.8)
arrow(ax,[4.2+np.cos(theta),8.5-np.cos(theta)],[10.5+np.sin(theta),5.8-np.sin(theta)],0.3,color='#8199bb')

arrow_with_rad(ax,[4.2,3.8],[10.5,6.8],1.9,0.3,color='#8199bb')

ax.text(10.5,8,r'${G_s}$',fontsize=20)

circle_with_text(ax,25.0,19.0,'$\mathrm{U_{1}}$',1)
circle_with_text(ax,35.0,17.0,'$\mathrm{U_{2}}$',1)
circle_with_text(ax,32.0,8.0,'$\mathrm{U_{3}}$',1)
circle_with_text(ax,24.0,10.0,'$\mathrm{U_{4}}$',1)

hexagon_with_text(ax,32.5,14.0,'$\mathrm{I_{1}}$',1)
hexagon_with_text(ax,23.0,16.0,'$\mathrm{I_{2}}$',1)
hexagon_with_text(ax,27.0,13.0,'$\mathrm{I_{3}}$',1)

theta=-np.pi/2-np.arctan2(35.0-25.0,17.0-19.0)
arrow(ax,[35.0+np.cos(theta),25.0-np.cos(theta)],[17.0+np.sin(theta),19.0-np.sin(theta)],0.3,color='#8199bb')

theta=-np.pi/2-np.arctan2(24.0-25.0,10.0-19.0)
arrow(ax,[24.0+np.cos(theta),25.0-np.cos(theta)],[10.0+np.sin(theta),19.0-np.sin(theta)],0.3,color='#8199bb')

theta=-np.pi/2-np.arctan2(24.0-32.0,10.0-8.0)
arrow(ax,[24.0+np.cos(theta),32.0-np.cos(theta)],[10.0+np.sin(theta),8.0-np.sin(theta)],0.3,color='#8199bb')

theta=-np.pi/2-np.arctan2(32.0-35.0,8.0-17.0)
arrow(ax,[32.0+np.cos(theta),35.0-np.cos(theta)],[8.0+np.sin(theta),17.0-np.sin(theta)],0.3,color='#8199bb')

theta=-np.pi/2-np.arctan2(25.0-32.0,19.0-8.0)
arrow(ax,[25.0+np.cos(theta),32.0-np.cos(theta)],[19.0+np.sin(theta),8.0-np.sin(theta)],0.3,color='#8199bb')

theta=-np.pi/2-np.arctan2(24.0-23-np.cos(np.pi*5/3),10.0-16.0-np.sin(np.pi*5/3))
arrow(ax,[24.0+np.cos(theta),23.0+np.cos(np.pi*5/3)],[10.0+np.sin(theta),16.0+np.sin(np.pi*5/3)],0.3,color='#b65576',linestyle='--')

theta=-np.pi/2-np.arctan2(32.0-32.5-np.cos(np.pi*4/3),8.0-14.0-np.sin(np.pi*4/3))
arrow(ax,[32.0+np.cos(theta),32.5+np.cos(np.pi*4/3)],[8.0+np.sin(theta),14.0+np.sin(np.pi*4/3)],0.3,color='#b65576',linestyle='--')

theta=-np.pi/2-np.arctan2(25.0-32.0-np.cos(np.pi*2/3),19.0-8.0-np.sin(np.pi*2/3))
arrow(ax,[25.0+np.cos(theta),27.0+np.cos(np.pi*2/3)],[19.0+np.sin(theta),13.0+np.sin(np.pi*2/3)],0.3,color='#b65576',linestyle='--')
arrow(ax,[25.0+np.cos(theta),32.5+np.cos(np.pi*3/3)],[19.0+np.sin(theta),14.0+np.sin(np.pi*3/3)],0.3,color='#b65576',linestyle='--')

theta=-np.pi/2-np.arctan2(24.0-23-np.cos(np.pi*5/3),10.0-16.0-np.sin(np.pi*5/3))
arrow(ax,[24.0+np.cos(theta),23.0+np.cos(np.pi*5/3)],[10.0+np.sin(theta),16.0+np.sin(np.pi*5/3)],0.3,color='#b65576',linestyle='--')

theta=-np.pi/2-np.arctan2(35.0-23-np.cos(np.pi*0/3),17.0-16.0-np.sin(np.pi*0/3))
arrow(ax,[35.0+np.cos(theta),23.0+np.cos(np.pi*0/3)],[17.0+np.sin(theta),16.0+np.sin(np.pi*0/3)],0.3,color='#b9b8bd',linestyle='--')

theta=-np.pi/2-np.arctan2(24.0-27-np.cos(np.pi*4/3),10.0-13.0-np.sin(np.pi*4/3))
arrow(ax,[24.0+np.cos(theta),27.0+np.cos(np.pi*4/3)],[10.0+np.sin(theta),13.0+np.sin(np.pi*4/3)],0.3,color='#b9b8bd',linestyle='--')

theta=-np.pi/2-np.arctan2(32.0-27-np.cos(np.pi*5/3),8.0-13.0-np.sin(np.pi*5/3))
arrow(ax,[32.0+np.cos(theta),27.0+np.cos(np.pi*5/3)],[8.0+np.sin(theta),13.0+np.sin(np.pi*5/3)],0.3,color='#b9b8bd',linestyle='--')

arrow_with_rad(ax,[25,24],[19,10],4.8,0.3,color='#8199bb')

bbox_props = dict(boxstyle="rarrow,pad=0.3", fc="#629cce", ec="#657084", lw=2)

ax.text(16, 18, " "*15, ha="center", va="center", rotation=345,
            size=15,
            bbox=bbox_props)

ax.text(16, 9, " "*15, ha="center", va="center", rotation=30,
            size=15,
            bbox=bbox_props)

arrow(ax,[10,13],[24.5,24.5],0.3,color='#b65576',linestyle='--')
arrow(ax,[20,23],[24.5,24.5],0.3,color='#b9b8bd',linestyle='--')
arrow(ax,[27,30],[24.5,24.5],0.3,color='#8199bb')

ax.text(9.5,24.5,'Purchase-P',fontsize=15,va='center',ha='right')
ax.text(19.5,24.5,'Purchase-N',fontsize=15,va='center',ha='right')
ax.text(26.5,24.5,'Trust',fontsize=15,va='center',ha='right')

fig=plt.gcf()
fig.set_size_inches(14, 8)

ax.set_xlim(0,40)
ax.set_ylim(0,25)

plt.show()

运行效果如下：