【AI测试】也许这有你想知道的人工智能(AI)测试--第四篇 --机器学习模型评估,算法测试
模型评估测试
Accuracy(准确率)
Precision(精确率)
Recall(召回率)
F1值
P-R(Precision-recall )曲线
ROC曲线
AUC值
Kappa系数
OOB误差
Accuracy、Precision、Recall
对于二值分类器,或者说分类算法,如分类猫和狗,分类性别男和女。
TP、FP、TN、FN,即:
True Positive, False Positive, True Negative, False Negative
预测值与真实值相同,记为T(True)
预测值与真实值相反,记为F(False)
预测值为正例,记为P(Positive)
预测值为反例,记为N(Negative)
TP:预测类别是正例,真实类别是正例
FP:预测类别是正例,真实类别是反例
TN:预测类别是反例,真实类别是反例
FN:预测类别是反例,真实类别是正例

计算举例: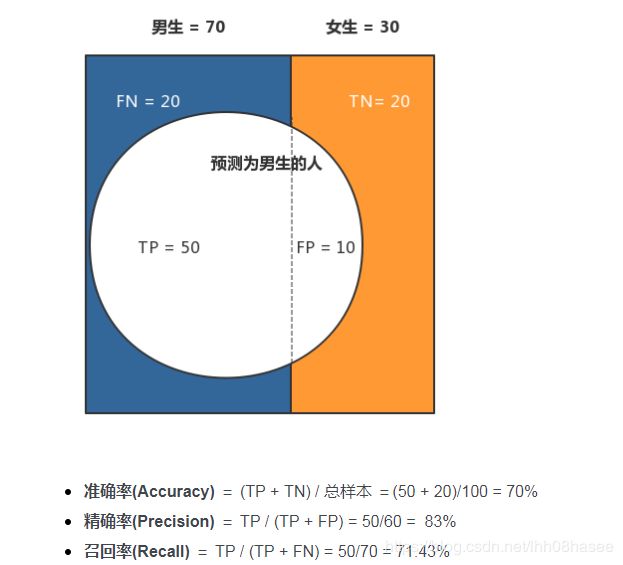
F1值
ROC曲线、AUC
受试者操作特征曲线(receiver operating characteristic curve),是反映敏感性和特异性连续变量的综合指标,roc曲线上每个点反映着对同一信号刺激的感受性。
要理解ROC曲线,先要了解TPR 和FPR
AUC
ROC曲线的面积就是AUC(Area Under the Curve)。AUC用于衡量“二分类问题”机器学习算法性能(泛化能力)。
样本中的真实正例类别总数即TP+FN。TPR即True Positive Rate
TPR = TP/(TP+FN)。
样本中的真实反例类别总数为FP+TN。FPR即False Positive Rate
FPR=FP/(TN+FP)
横轴:FPR
代表分类器预测的正类中实际负实例占所有负实例的比例。
纵轴:TPR
代表分类器预测的正类中实际正实例占所有正实例的比例。
sklearn接口文档代码示例
import numpy as np
import matplotlib.pyplot as plt
from itertools import cycle
from sklearn import svm, datasets
from sklearn.metrics import roc_curve, auc
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import label_binarize
from sklearn.multiclass import OneVsRestClassifier
from scipy import interp
# Import some data to play with
iris = datasets.load_iris()
X = iris.data
y = iris.target
# Binarize the output
y = label_binarize(y, classes=[0, 1, 2])
n_classes = y.shape[1]
# Add noisy features to make the problem harder
random_state = np.random.RandomState(0)
n_samples, n_features = X.shape
X = np.c_[X, random_state.randn(n_samples, 200 * n_features)]
# shuffle and split training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.5,
random_state=0)
# Learn to predict each class against the other
classifier = OneVsRestClassifier(svm.SVC(kernel='linear', probability=True,
random_state=random_state))
y_score = classifier.fit(X_train, y_train).decision_function(X_test)
# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
fpr[i], tpr[i], _ = roc_curve(y_test[:, i], y_score[:, i])
roc_auc[i] = auc(fpr[i], tpr[i])
# Compute micro-average ROC curve and ROC area
fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), y_score.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])
plt.figure()
lw = 2
plt.plot(fpr[2], tpr[2], color='darkorange',
lw=lw, label='ROC curve (area = %0.2f)' % roc_auc[2])
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()
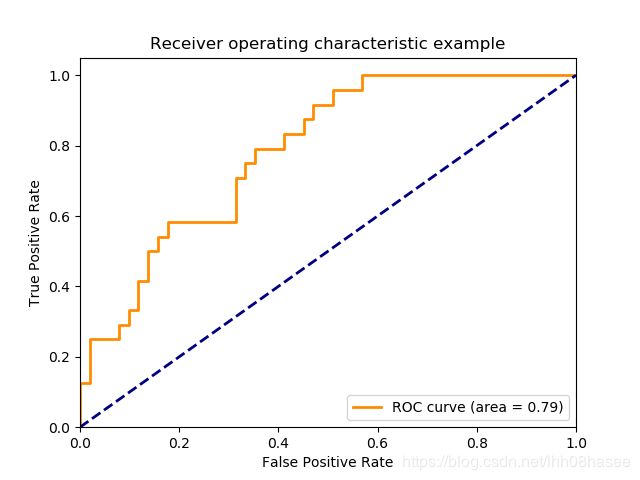
sklearn.metrics中的评估方法介绍(accuracy_score, recall_score, roc_curve, roc_auc_score, confusion_matrix)
https://blog.csdn.net/CherDW/article/details/55813071
P-R曲线
P-R曲线用来衡量分类器性能的优劣,横轴为recall ,纵轴为precision。
P-R 曲线越靠近右上角性能越好。
如果有多个分类器,则可以画出P-R曲线,若一个分类器A的P-R曲线把另外一个分类器B覆盖,则在一方面可以说明 A的分类器性能比B分类器好。
有交叉时,用平衡点(BEP)来衡量。平衡点即precision 等于 recall 时的值。那么可以认为A优于B。
画出P-R曲线:
算法对样本进行分类时,通常都会有个阈值,或者超参数,需要调。
不同的阈值时,就可以得出不同的精确率和召回率,从而画出P-R曲线图。

平衡点还是过于简化,于是有了 F1 值这个新的评价标准,它是精确率和召回率的调和平均值。
ROC曲线和P-R曲线的选择
ROC曲线由于兼顾正例与负例,所以适用于评估分类器的整体性能,相比而言PR曲线完全聚焦于正例。
如果有多份数据且存在不同的类别分布,如果想测试不同类别分布下对分类器的性能的影响,则PR曲线比较适合。
Kappa系数
Kappa系数是一种度量分类结果一致性的统计量, 是度量分类器性能稳定性的依据, Kappa系数值越大, 分类器性能越稳定。
kappa系数是用在统计学中评估一致性的一种方法,我们可以用他来进行多分类模型准确度的评估,这个系数的取值范围是[-1,1],实际应用中,一般是[0,1]
0.0~0.20极低的一致性(slight)
0.21~0.40一般的一致性(fair)
0.41~0.60 中等的一致性(moderate)
0.61~0.80 高度的一致性(substantial)
0.81~1几乎完全一致(almost perfect)
几个数字解释,帮忙更好理解:
664 = 239+ 16+6 + 21 +73+9 + 16+4+280
261 = 239+16+6
276 = 239+21+16
python代码实现
import numpy as np
def kappa(matrix):
n = np.sum(matrix)
sum_po = 0
sum_pe = 0
for i in range(len(matrix[0])):
sum_po += matrix[i][i]
row = np.sum(matrix[i, :])
col = np.sum(matrix[:, i])
sum_pe += row * col
po = sum_po / n
pe = sum_pe / (n * n)
return (po - pe) / (1 - pe)
matrix = [
[239, 21, 16],
[16, 73, 4],
[6, 9, 280]]
matrix = np.array(matrix)
print(kappa(matrix))
输出结果 0.823444037801766
OOB误差
随机森林算法利用OOB误差估计作为对预测误差的无偏估计, 评估模型性能, 值越小, 说明模型精度越高。

只是用于 随机森林算法。

