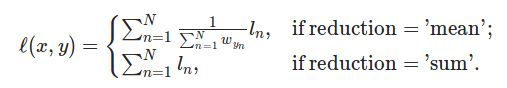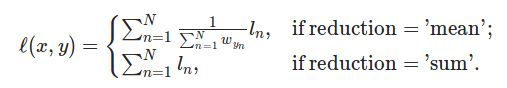TensorFlow 和 Pytorch 中交叉熵 Cross Entropy Loss 的代码实现和手动实现方式

TensorFlow中交叉熵的实现

手动实现

import tensorflow as tf
# logits 为输出层输出
logits = tf.constant([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]])
# softmax
soft_y = tf.nn.softmax(logits)
# label y_
y_ = tf.constant([[0.0, 0.0, 1.0], [0.0, 0.0, 1.0], [0.0, 0.0, 1.0]])
# negative log 
neg_soft_log= y_ * tf.log(soft_y)
# cross entorpy
cross_entropy = -tf.reduce_sum(neg_soft_log)

调库实现

# softmax_cross_entropy_with_logits
soft_ce_logits=tf.nn.softmax_cross_entropy_with_logits_v2(logits=logits, labels=y_)
# sum all negitive log
cross_entropy_tf = tf.reduce_sum(soft_ce_logits)

代码验证

with tf.Session() as sess:
    softmax = sess.run(soft_y)
    ce = sess.run(cross_entropy)
    ce_tf = sess.run(cross_entropy_tf)
    print('softmax(y):')
    print(softmax)
    print()
    print('negative log: - y_ * log(y)')
    print(sess.run(neg_soft_log))
    print()
    print("softmax result")
    print(ce)
    print()
    print('soft cross entropy logits:')
    print(sess.run(soft_ce_logits))
    print("softmax_cross_entropy_with_logits")
    print(ce_tf)

输出结果

softmax(y):
[[0.09003057 0.24472848 0.66524094]
 [0.09003057 0.24472848 0.66524094]
 [0.09003057 0.24472848 0.66524094]]
 
 negative log: - y_ * log(y)
[[-0.         -0.         -0.407606  ]
 [-0.         -0.         -0.407606  ]
 [-0.         -0.         -0.40760598]]
 
softmax result
1.222818

soft cross entropy logits:
[0.40760595 0.40760595 0.40760595]
softmax_cross_entropy_with_logits
1.2228179

Pytorch中交叉熵的实现

手动实现

y = torch.Tensor([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]])
# softmax
soft_y = torch.nn.Softmax(dim=-1)(y)
print("step1:softmax result=")
print(soft_y)
print()
# label  y_
y_ = torch.Tensor([[0.0, 0.0, 1.0], [0.0, 0.0, 1.0], [0.0, 0.0, 1.0]])
log_soft_y=torch.log(soft_y)
print('log soft y:')
print(log_soft_y)
print()
ce=-torch.mean(y_*log_soft_y)
print('tf way ce: ', ce)
y_2 = torch.LongTensor([2, 2, 2])
ce_torch=torch.nn.NLLLoss()(log_soft_y,y_2)
print('torch way ce :',ce_torch)

调库实现

ce_loss_torch=torch.nn.CrossEntropyLoss()(y,y_2)
print('ce in torch nn')
print(ce_loss_torch)

输出结果

softmax result=
tensor([[0.0900, 0.2447, 0.6652],
        [0.0900, 0.2447, 0.6652],
        [0.0900, 0.2447, 0.6652]])

log soft y:
tensor([[-2.4076, -1.4076, -0.4076],
        [-2.4076, -1.4076, -0.4076],
        [-2.4076, -1.4076, -0.4076]])
        
tf way ce:  tensor(0.1359)
torch way ce : tensor(0.4076)
ce in torch nn
tensor(0.4076)

结论

TensorFlow 没有求平均，Pytorch对输出结果求了平均！