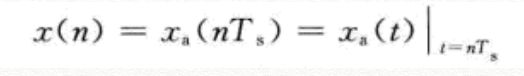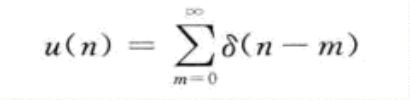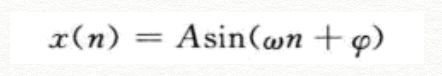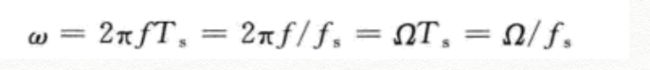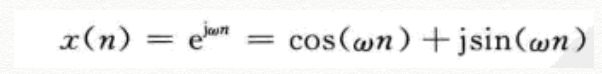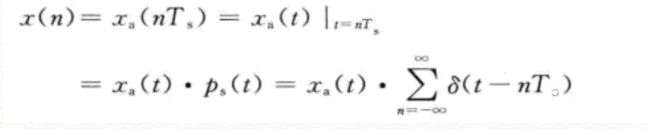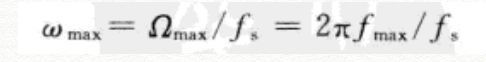数字信号入门笔记1 — 离散时间信号
数字信号入门笔记1 — 离散时间信号
目录
数字信号入门笔记1 — 离散时间信号
知识点提要:
1.1信号的概念与分类
1.2信号时域描述
1.3信号频域描述
1.3.1采样与混叠
1.3.2信号恢复
本节主要记录数字信号相关概念,常见信号,信号的描述方法(时域描述/频域描述),以及模型信号和数字信号转换及其中产生的问题。
知识点提要:
- 单位冲击信号的时域描述,作为最基本的离散时域信号,可以表示其他离散时域信号。
- 模拟角频率单位为Hz,代表每秒转多少周期 模拟角频率Ω代表每秒转到少弧度(rad/s). 数字频率w 每个采样点间弧度rad
- 复正弦信号由欧拉公式得到,建立了三角函数和复向量间关系,常用于代码实现信号相关算法
- DTFT(区别于DFT ) 离散信号的DTFT是连续的(数字频率w为连续的)
- 时域采样->频谱混叠->周期延拓 频域解释-w周期为2Pi 时域解释-由采样点可以恢复出不同频率的正弦信号
- 采样与奈奎斯特采样定理解释
- 数字信号恢复到模拟信号
1.1信号的概念与分类
信号是携带信息的物理量或物理现象。信号通常是随时间变化的有限实函数,满足“实值性”和“有限性”。
实值性
自然界大部分信号是连续变化的模拟信号,其取值都是实数,目前自然界还没有发现复信号,不是整数或复数。但是信号处理中大量用到了复数,是因为复数可以简化运算。
有限性
信号的值必须有限。
常见信号分类方法
1.确定信号与随机信号。
2.连续时间信号与离散时间信号。
3.模拟信号与数字信号。
1.2信号时域描述
离散时间信号指离散时间有定义的信号,若从模拟信号均匀采样得到,则可以表示为:
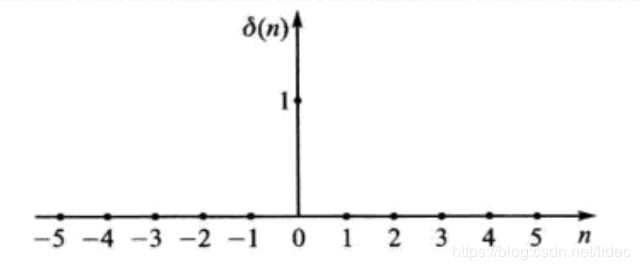
可以理解为每隔Ts时间采样一次Xa下面介绍几个典型信号的时域描述,特别要注意单位冲击信号,可以用单位冲击信号表征其他信号或系统。单位冲击信号,也称单位抽样信号,定义如下:
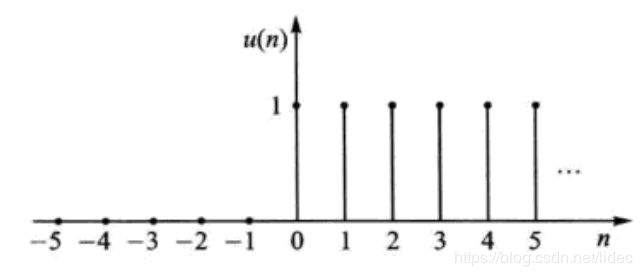
是最基本的离散时间信号。这里需要注意,在连续信号中,冲击信号是时间无限短,幅度无限大的,但是在离散信号中,单位冲击信号赋值为1。单位阶跃信号是单位冲击信号的求和,可以表示为如下公式:
或
其中A为幅度,fi为初相,w为角速度,也称为数字频率,单位是弧度,表征信号变化快慢。上式可以看作是由下式的模拟信号采样而来
其中f成为模拟频率,Ω=2*Pi*f称为模拟角频率,单位rad/s,我理解为把信号周期T映射到2Pi上,Ts为采样周期。可以理解为吧2Pif每隔Ts取一个点。
复正弦信号建立了三角函数和复指数函数的关系,这里是由欧拉公式得到,可以用它来表征线性时不变系统,同时也是傅立叶变换的基函数。另外在代码实现时,可以用三角函数和虚数的这种方式来表示一个向量。
1.3信号频域描述
离散信号傅立叶变换称为离散时间傅立叶变换(DTFT)
如果离散信号x(n)绝对可和,则其DTFT存在且连续。这里可以看到,每个DTFT值都是随数字频率w变化的,W是连续变化,所以虽然是离散信号x(n) ,但是它的DTFT确是连续的。另外,w是以2Pi为周期的,所以DTFT的结果也是周期性的。x(n)可以看作是由连续模拟信号xa(t) 采样得到,DTFT结果则可以看作是xa(t) 频谱的周期延拓。这里是从频域角度(数字频率w是周期性的角度)来说明为什么时域采样信号经过DTFT到了频域,频域会出现周期延拓。
1.3.1采样与混叠
下面从是时域角度说明为什么时域采样后频域会周期延拓(或者说为什么时域采样后会对应多个频域值,而且这些频域值还是周期性的)。从下图看,不同频率的正弦信号,时域采样后可能结果是一样的。下图中如果一次采样6个点,只能恢复出曲线2正弦对应频率,必须增加采点数,也就是提高采样频率,才能恢复出真实的曲线1的正弦信号。这种由采样导致的不确定性,称为混叠。
C中高频信号实际位7个周期,频率为7,如果采样频率为6HZ,那么采到的信号恰好为1个周期,也就是通过采样后恢复的信号是一个1Hz的正弦信号,这样显然是错的。
采样频率一般需要一些先验知识,比如人耳可以听到最高频率为20kHz左右,所以音频信号一般最高采样率为44100Hz,这样就可以恢复到录音时所有人耳可以听到的频率。那么需要把采样频率提升到多少才能完全恢复出原始信号呢?至此,大家肯定想到了奈奎斯特采样定理,也就是采样频率必须高于信号频率的2倍。
下面是一个比较傻但是经常犯疑问的问题。如果给一个随机的周期信号,是否只要采样频率为随机周期信号频率的2倍以上,就可以恢复这个随机周期信号呢?显然不是,这里可以恢复的都是单频的正弦信号。那么不能恢复随机的周期信号,采样定理由什么用呢?由傅立叶级数知道任何信号都可以分解为正弦信号,所以一般会把时域信号变换到频域,当成多个正弦信号的叠加,处理好单个的正弦信号,复杂信号由傅立叶反变换回即可。所以如果想恢复这段随机的周期信号,采样频率必须大于其中最高频率正弦信号频率的2倍。
下面回到主线,需要把采样频率提升到多少才能完全恢复出原始信号呢?这里需要先看一下采样的数学解释:
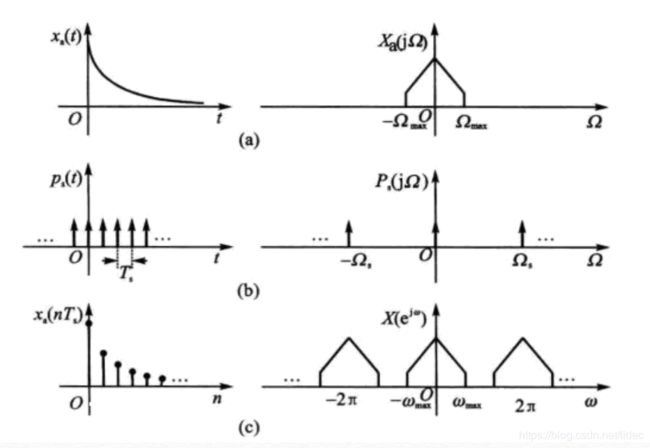
采样的过程相当于模拟信号与一串单位冲击信号相乘,
a为模拟信号xa(t)和这个信号对应的频谱。Ωmax是最大角频率,对应xa(t)的最大频率为fmax = Ω/2Pi。
b为单位冲击信号和其对应的频域,冲激串的频谱依然是冲击串,时域间隔Ts,频域间隔Ωs。Ωs=2Pi/Ts=2*Pi*fs。可以理解为采样点得到的频率可以是真正频率的周期倍数。对应到w就是每次踩点对应到转过多少rad,整数周期对应到rad也就是2π。Ω是每秒转过多少弧度,fs是每秒采样多少点,w=Ω/fs,把每秒转过的角度归到每个采样点上,是对Ω在采样频率上的映射,也就是每采样一个点转过的角度,采样频率越大,w越小,越不容易混叠。
c相当于模拟信号与采样信号时域相乘,做傅立叶变换对应的频谱。
1.3.2信号恢复
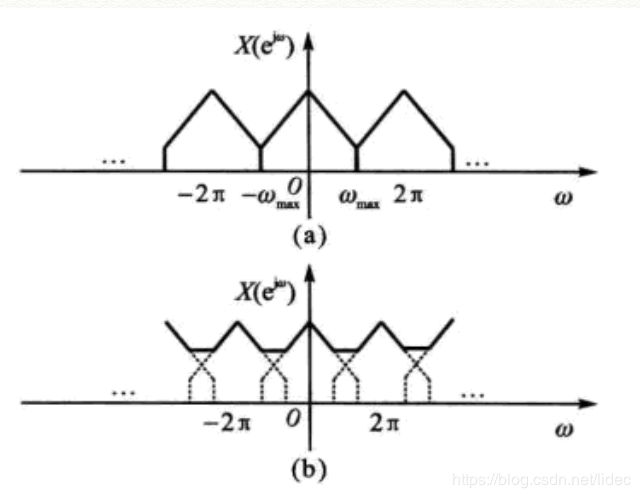
下面是模拟角频率Ω(rad/s)与w数字频率的对应关系,模拟角频率/采样频率得到的结果就是数字频率。
这里采样频率fs会决定数字频率的大小。如果fs太小,也就是采样率低,那么最大的数字频率就会增加。这里根据wmax=2*Pi*fmax/fs可知,当fs=2*fmax的时候,频谱延拓的区域刚好相接 如下图a,如果fs<2*fmax,则wmax会增大,导致频域发生重叠,如下图b。
谈完了采样,在看一下恢复,也就是数字信号恢复成模拟信号时遇到的问题。由上文可知,在满足采样定理的条件下,模拟信号和数字信号包含的信息是一样的,另一方面,采样得到数字信号的频谱是延拓的,这样就会导致除了真正的信号,还可能包含相位相差2Pi的高频信号。所以在输出时需要一个低通滤波器,在频域上圈住-Pi~Pi的范围,这样就去除了高频延拓,用这样的频域信号恢复到时域就是原先的时域信号。
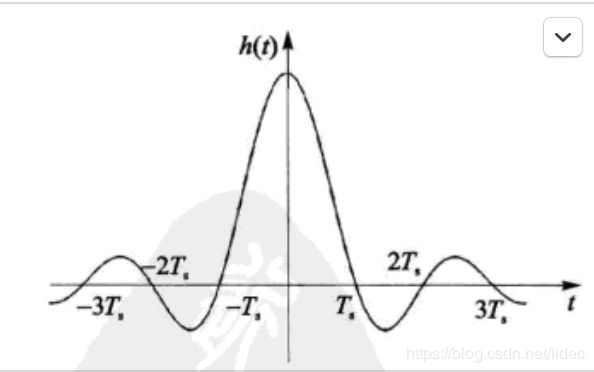
上图虚线理想重构器就是一个这样的低通滤波器。这个方块滤波器在时域的波形如下
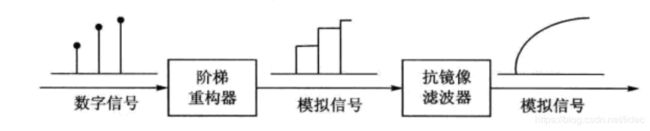
也就是说恢复成模拟信号后,相当于需要在时域卷积一个上图类型的信号,相当于进行一次低通滤波。这里需要记一个结论,形如上图的波形和矩形框这种的波形互为傅立叶变换对,后面还会多次用到这个结论。实际恢复过程中,由于保持器恢复的时候还会引入高频,一般处理流程是在保持器后增加一个叫做康镜像滤波器的低通滤波器。