跨媒体检索(关联)之基于CCA的方法大总结
跨媒体检索相关英文论文下载地址
文章目录
- 背景
- 1 2010-A New Approach to Cross-Modal Multimedia Retrieval[1]
- 1.1 主要思想
- 1.2 模型
- 1.2.1 问题
- 1.2.2 CM
- 1.2.3 SM
- 1.2.4 SCM
- 1.3 实验
- 1.4 讨论
- 2 2013-Deep Canonical Correlation Analysis[2]
- 2.1 主要思想
- 2.2 KCCA
- 2.3 DCCA
- 2.4 实验
- 3 2014-Cluster Canonical Correlation Analysis[4]
- 3.1主要思想
- 3.2 模型
- 3.3 实验
- 3.3.1 数据集
- 3.3.2 预处理和结果
- 3.4 结论
- 4 2014-On the Role of Correlation and Abstraction in Cross-Modal Multimedia Retrieval[5]
- 4.1 主要思想
- 4.2 模型
- 4.2.1 相关匹配(CM)
- 4.2.2 语义匹配(SM)
- 4.2.3 语义相关篇匹配(SCM)
- 4.3 实验
- 4.4 讨论
- 5 2015- Multi-Label Cross-modal Retrieval[6]
- 5.1 主要思想
- 5.2 模型
- 5.3 多标签典型相关分析算法(Multi-Label C anonical Correlation Analysis,ml-CCA)
- 5.4 实验
- 参考文献
背景
跨媒体既表现为包括文本、图像、音频、视频等媒体类型混合并存,又表现为各种媒体类型形成复杂的关联关系和组织结构。如何在不同媒体之间建立一种联系使得能够统一的表达跨媒体信息是目前跨媒体研究的一个重要挑战。
常见的方法是建立一个共享子空间,不同媒体类型的数据对象的相似性可以映射到这个子空间中使用常见的距离度量(如欧几里得和余弦距离)算法直接计算。
本文依据几篇经典的论文,介绍了几种基于典型相关分析(CCA)的方法。
1 2010-A New Approach to Cross-Modal Multimedia Retrieval[1]
1.1 主要思想
本文研究多媒体文本和图像联合建模问题。
- 表示:
文本使用LDA(latent Dirichlet allocation)模型表示。
图像使用SIFT特征表示。 - 学习模型:CM/SM/SCM
- 数据集:Wikipedia dataset.
- 创新之处:
提出三种子空间学习模型。
增加语义层的推断。例如,将层次主题模型用于文本聚类或层次语义表示用于图像检索。通过将图像和文档利用逻辑回归算法建模为关于一组预定义文档类的后验概率向量,并与通过CCA学习后的子空间联合,提出一个语义相关匹配(SCM)跨媒体检索模型。
1.2 模型
1.2.1 问题
在 R I 和 R T R^I和R^T RI和RT特征空间中表示图像和文本向量,每个文档和图像与各自的空间中的点建立一对一的映射。目标是给定一个查询文本(图像) T q ∈ R T ( I q ∈ R I ) T_q ∈R^T(I_q ∈R^I) Tq∈RT(Iq∈RI),检索模型在图像空间 R I R^I RI(文本空间 R T R^T RT)中返回最相近的匹配。
一般情况下,在 R I R^I RI和 R T R^T RT建立一个可逆映射,如:
M : R T → R I M: R^T→R^I M:RT→RI
给定一个 T q i n R T T_q \ in\ R^T Tq in RT,返回一个最近匹配 M ( T q ) i n R I M(T_q ) \ in\ R^I M(Tq) in RI,反之同。
但由于文本和图像的表示方法不同,因此上述表示不能直接建立。一种方法是,建立两个中间空间用来映射这两种表示,如:
M I : R I → U I M_I: R^I→U^I MI:RI→UI M T : R T → U T M_T: R^T→U^T MT:RT→UT
U I , U T U^I,U^T UI,UT 空间是同构的,因此可以建立一个映射,如:
M : U T → U I . M: U^T→U^I. M:UT→UI.
给定一个 T q i n R T T_q \ in\ R^T Tq in RT。返回最近匹配 M I − 1 ∘ M ∘ M T ( T q ) i n R I M_I^{-1}∘M∘M_T (T_q ) \ in\ R^I MI−1∘M∘MT(Tq) in RI,反之,给定 I q i n R I I_q \ in\ R^I Iq in RI,返回 M T − 1 ∘ M − 1 ∘ M I ( I q ) i n R T . M_T^{-1}∘M^{-1}∘M_I (I_q ) \ in\ R^T. MT−1∘M−1∘MI(Iq) in RT.
所以在这种情况下,目标是学习 U I , U T U^I,U^T UI,UT。
论文提出3种方法,分别是 C o r r e l a t i o n m a t c h i n g ( C M ) Correlation matching(CM) Correlationmatching(CM), S e m a n t i c m a t c h i n g ( S M ) Semantic matching(SM) Semanticmatching(SM), S e m a n t i c c o r r e l a t i o n m a t c h i n g ( S C M ) Semantic correlation matching(SCM) Semanticcorrelationmatching(SCM).
1.2.2 CM
第一种方法,建立两个线性投影矩阵:
P T : R T → U T P_T: R^T→U^T PT:RT→UT P I : R I → U I P_I: R^I→U^I PI:RI→UI
分别将 R I , R T R^I,R^T RI,RT映射到相关的d维子空间 U I , U T U^I,U^T UI,UT,其维持了表示的抽象层级。
这里使用了典型相关分析(Canonical correlation analysis ,CCA)方法学习子空间 U I ⊂ R I U^I⊂R^I UI⊂RI, U T ⊂ R T U^T⊂R^T UT⊂RT。CCA是一种类似于PCA的数据分析和降维方法,和PCA不同的是CCA可以对两个空间进行降维,并提供相同的异构表示。
定义 w i ∈ R I , w t ∈ R T w_i∈R^I,w_t∈R^T wi∈RI,wt∈RT,目标是最大化文本和图像变量的相关性,如,
max w i ≠ 0 , w t ≠ 0 w i T ∑ I T w t w i T ∑ I I w i w t T ∑ T T w t (1-1) \max_{w_i\neq0,w_t\neq0} \frac{w_i^T\sum_{IT}w_t} {\sqrt{w_i^T\sum_{II}w_i}\sqrt{w_t^T\sum_{TT}w_t}} \tag{1-1} wi=0,wt=0maxwiT∑IIwiwtT∑TTwtwiT∑ITwt(1-1)
∑ I I \sum_{II} ∑II 和 ∑ T T \sum_{TT} ∑TT分别表示图像 I 1 , . . . , I ( ∣ D ∣ ) {I_1,...,I_(|D|)} I1,...,I(∣D∣) 和文本${T_1,…,T_(|D|)} 经 验 协 相 关 矩 阵 ∑ I T 经验协相关矩阵\sum_{IT} 经验协相关矩阵∑IT = = = ∑ T I T \sum_{TI}^T ∑TIT是其交叉-协相关矩阵。
公式(1-1)可以转化为一个一般的求特征值的问题(generalized eigenvalue problem,GEV)。首先利用LDA优化问题,固定分母,求分子最大化。如:
m a x i m i z e w i T ∑ I T w t s . t . w i T ∑ I I w i = 1 , w t T ∑ T T w t = 1 (1-2) max \ imize \ w_i^T\sum_{IT}w_t \\ s.t. \ w_i^T\sum_{II}w_i=1,w_t^T\sum_{TT}w_t=1 \tag{1-2} max imize wiTIT∑wts.t. wiTII∑wi=1,wtTTT∑wt=1(1-2)
求解此问题可以用拉格朗日乘数法,令:
L = w i T ∑ I T w t − λ 2 ( w i T ∑ I I w i − 1 ) − θ 2 ( w t T ∑ T T w t − 1 ) , (1-3) L = w_i^T\sum_{IT}w_t - \frac {\lambda}{2}({w_i^T\sum_{II}w_i-1})-\frac {\theta}{2}(w_t^T\sum_{TT}w_t-1) , \tag{1-3} L=wiTIT∑wt−2λ(wiTII∑wi−1)−2θ(wtTTT∑wt−1),(1-3)
对(1-3)求偏导,得到 ∂ L ∂ w i \frac{\partial L} {\partial w_i} ∂wi∂L和 ∂ L ∂ w t \frac{\partial L} {\partial w_t} ∂wt∂L,令其等于0,得:
{ ∑ I T w t − λ ∑ I I w i = 0 , ∑ T I w i − θ ∑ T T w t = 0. (1-4) \begin{cases} \sum_{IT}w_t-\lambda \sum_{II}w_i=0,\\\sum_{TI}w_i-\theta \sum_{TT}w_t=0. \end{cases} \tag{1-4} {∑ITwt−λ∑IIwi=0,∑TIwi−θ∑TTwt=0.(1-4)
公式(1-4)可以转化为一个求特征值问题,简化得:
( 0 ∑ I T ∑ T I 0 ) ( w i w t ) = λ ( ∑ I I 0 0 ∑ T T ) ( w i w t ) . (1-5) \begin{pmatrix} 0 & \sum_{IT} \\\\ \sum_{TI} & 0 \\ \end{pmatrix} \begin{pmatrix} w_i \\\\ w_t \\ \end{pmatrix} = \lambda \begin{pmatrix} \sum_{II} &0 \\\\ 0 & \sum_{TT}\end{pmatrix} \begin{pmatrix} w_i \\\\ w_t \\ \end{pmatrix}. \tag{1-5} ⎝⎛0∑TI∑IT0⎠⎞⎝⎛wiwt⎠⎞=λ⎝⎛∑II00∑TT⎠⎞⎝⎛wiwt⎠⎞.(1-5)
最终求出 λ λ λ和 w i , w t w_i,w_t wi,wt.
应用于跨媒体检索中,每个文本 T ∈ R T T∈ R^T T∈RT被映射到其投影 p T = P T ( T ) p_{T}=P_T (T) pT=PT(T)到 w ( t , k ) k = 1 d {w_(t,k)}_{k=1}^d w(t,k)k=1d上,图像与之类似。这样向量 p T p_T pT和 p I p_I pI分别是两个同构d维子空间 U T 和 U I U^T和U^I UT和UI的坐标,它们也被认为是属于通过 U T U^T UT和 U I U^I UI叠加而形成的单个空间 U U U.
给定一个图像 I q I_q Iq,且 p I = P ( I q ) p_I=P(I_q) pI=P(Iq),目标是求使得公式(1-6)最小的 p T = P T ( T ) p_T=P_T (T) pT=PT(T)的值 ( T ∈ R T ) (T ∈ R^T) (T∈RT),并返回最相似的匹配 T T T,式(1-6)如下:
D ( I , T ) = d ( p I , p T ) (1-6) D(I,T)= d(p_I,p_T) \tag{1-6} D(I,T)=d(pI,pT)(1-6)
式(1-6)中 d d d是一种距离度量公式。
以上检索类型被定义为 c o r r e l a t i o n m a t c h i n g correlation matching correlationmatching.
1.2.3 SM
第二种方法,建立两个非线性转换:
L T : R T → S T L_T: R^T→S^T LT:RT→ST L I : R I → S I L_I: R^I→S^I LI:RI→SI
将 R I , R T R^I,R^T RI,RT映射到一对语义空间 S T , S I , s . t . S T = S I S^T, S^I, s.t. S^T= S^I ST,SI,s.t.ST=SI。其增加了表示的语义抽象。
首先在数据库中定义语义概念词典 V = { v 1 , … , v K } V=\lbrace{ v_1,…,v_K }\rbrace V={v1,…,vK},其中 v K v_K vK表示一个类,比如“History” 或者 “Biology”。
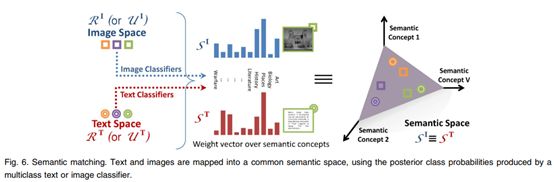
L T L_T LT 将一个文本 T ∈ R T T \in R^T T∈RT映射到一个后验概率向量 P ( V ∣ T ) ( v i │ T ) , i ∈ { 1 , … , K } P_(V|T) (v_i│T),i∈\lbrace{1,…,K}\rbrace P(V∣T)(vi│T),i∈{1,…,K}.这些向量构成一个语义空间 S T S^T ST,类似地,图像的语义空间为 S I S^I SI。
一种求后验概率分布的方法是多类逻辑回归算法。逻辑回归通过训练数据得到一个回归函数,从而计算一个类j的后验概率。回归函数公式如下:
P V ∣ X ( j ∣ x ; w ) = 1 Z ( x , w ) e x p ( w j T x ) (1-7) P_{V|X}(j|x;w)=\frac{1}{Z(x,w)}exp(w_j^Tx) \tag{1-7} PV∣X(j∣x;w)=Z(x,w)1exp(wjTx)(1-7)
其中 Z ( x , w ) = ∑ j e x p ( w j T x ) Z(x,w)=∑_jexp(w_j^T x) Z(x,w)=∑jexp(wjTx) 是归一化常数, V V V代表类别集合, X X X是输入的特征向量集合, w j w_j wj是类 j j j的参数向量。
由于 S T S^T ST 和 S I S^I SI 在相同的文档类中表示的后验概率向量空间,因此 S T S^T ST和 S I S^I SI是同构的,即认为 S T = S I S^T=S^I ST=SI。
给定一个图像 I q I_q Iq,将其表示为概率向量 π I ∈ S I π_I∈S^I πI∈SI,通过最小化公式(1-8)得到 π T ∈ S T π_T∈S^T πT∈ST,公式如下:
D ( I , T ) = d ( π I , π T ) (1-8) D(I,T)=d(\pi_I,\pi_T) \tag{1-8} D(I,T)=d(πI,πT)(1-8)
这种检索类型被定义为 s e m a n t i c m a t c h i n g semantic matching semanticmatching。
1.2.4 SCM
第三种方法,将1,2联合。
首先,使用CCA学习子空间 U I ⊂ R I , U T ⊂ R T U^I⊂R^I,U^T⊂R^T UI⊂RI,UT⊂RT,然后用逻辑回归算法在第一步基础上学习语义空间 S T S^T ST 和 S I S^I SI,最后根据公式(1-8)检索,其中 π I = L I ( P I ( I ) ) , π T = L T ( P T ( T ) ) π_I=L_I (P_I (I)), π_T=L_T (P_T (T)) πI=LI(PI(I)),πT=LT(PT(T)).
这种检索类型被定义为 s e m a n t i c c o r r e l a t i o n m a t c h i n g ( S C M ) semantic correlation matching (SCM) semanticcorrelationmatching(SCM).
1.3 实验
1.4 讨论
CCA方法只能解决线性表示的数据,Hwang[3]等人提出KCCA,可以表示非线性数据。
KCCA相对CCA的优势是:
- 由于其复杂的函数空间,使用足够的训练数据可以用来表示更高的相关性。
- 可以生成特征以提高分类器性能。
不足: - 训练速度慢。
- 测试时需要用到训练集,因此事先要存储训练集。
- 模型难以解释。
以上参考网站
2 2013-Deep Canonical Correlation Analysis[2]
2.1 主要思想
本文提出DCCA。实验表明,相比于CCA和KCCA,使用DCCA在相关性测量上具有更好的表示。
2.2 KCCA
原论文见[3],关于KCCA的详细原理见博客。
普通的线性CCA只能探索两组随机变量之间的线性关系,而在实际情况中,变量间的关系往往是非线性的,于是非线性的CCA出现了,KCCA就是一种常用的非线性CCA算法。
KCCA是把核函数的思想引入CCA中,思想是把低维的数据映射到高维的特征空间(核函数空间),并通过核函数方便地在核函数空间进行关联分析。
2.3 DCCA
KCCA方法虽然解决了数据的非线性问题,但是由于其核函数选取的不可知性,训练开销较大,模型较为复杂,因此DCCA被提出以解决这些问题。
神经网络解决非线性问题的时候,是通过嵌入每个层次的非线性函数来解决的,Deep CCA就是先用深度神经网络分别求出两个视图的经过线性化的向量,然后求出两个投影向量的最大相关性,最后求出新的投影向量。用这个投影向量加入到机器学习算法进行分类,聚类回归。
关于DCCA的详细原理见博客和原论文[2]。
2.4 实验
DCCA也能解决非线性问题,论文中的实验室在2种数据集(MNIST handwritten digits和Articulatory speech data)上进行,在这两个数据集上做相关性测试。结果略。
3 2014-Cluster Canonical Correlation Analysis[4]
3.1主要思想
本文解决了CCA要求数据必须是配对的条件限制。何为配对限制?一句话解释即运用CCA算法处理两个模态的数据时,必须一个文本对应一个图像且同时处理。
本文提出的cluster-CCA、mean-CCA和cluster-KCCA可以解决上述问题。
关于以上提到的几种方法,图3.1可以帮助我们更好的理解。
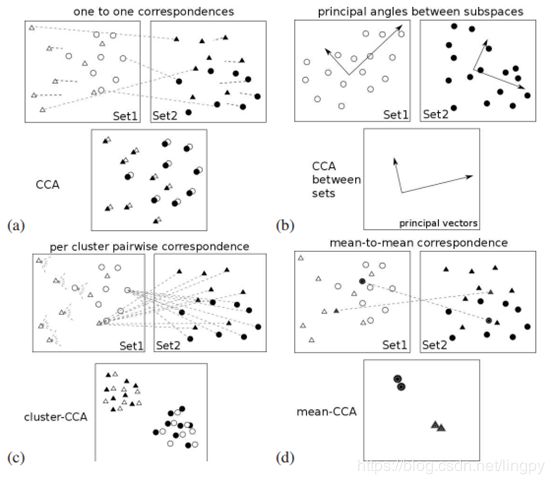
- CCA:使用集合之间的成对对应关系,不能分离两个集合
- CCA for sets:计算两个子空间之间的主角,不能处理多个集合
- cluster-CCA:使用集群内的所有成对对应
- Mean-CCA:计算平均聚类向量之间的CCA
3.2 模型
有两组数据,每组数据分为C个不同但相互对应的类,令 T x = { X 1 , X 2 , … , X C } T_x=\lbrace{X_1,X_2,…,X_C}\rbrace Tx={X1,X2,…,XC}和 T y = { Y 1 , Y 2 , … , Y C } T_y=\lbrace{Y_1,Y_2,…,Y_C}\rbrace Ty={Y1,Y2,…,YC},其中 X c = { x 1 C , … , x ∣ X c ∣ C } X_c=\lbrace{x_1^C,…,x_{|X_c|}^C}\rbrace Xc={x1C,…,x∣Xc∣C}和 Y c = { y 1 C , … , y ∣ Y c ∣ C } Y_c=\lbrace{y_1^C,…,y_{|Y_c |}^C}\rbrace Yc={y1C,…,y∣Yc∣C}分别为集合中第C类的数据点。
通过选择方向 w w w和 v v v找到 X X X和 y y y的新坐标,使得 T x T_x Tx和 T y T_y Ty在 w w w和 v v v上的投影有最大的相关性,同时,类之间可以很好地分离。但是无法直接计算这些投影之间的相关性,因为他们在 w w w和 v v v上的投影没有任何直接的对应关系。因此提出了Mean-CCA与Cluster-CCA。
关于这两个模型的详细解释参考博客。
3.3 实验
3.3.1 数据集
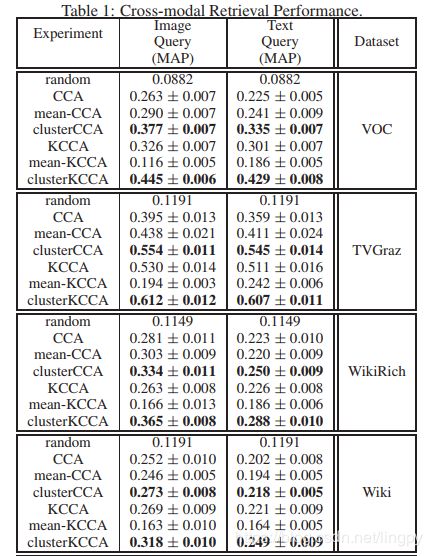
本文使用了5种数据集:Pascal VOC 2007, TVGraz, Wiki Text-Image Dataset, Heterogeneous Face Biometrics (HFB) and Materials Dataset.
3.3.2 预处理和结果
举例,预处理wiki数据集,采用10-主题LDA模型提取文本特征,dense SIFT BOW提取图像特征。
跨媒体检索-PR曲线
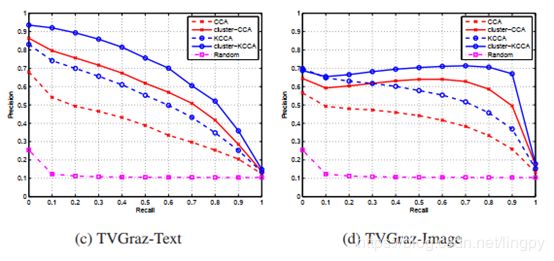
从图3.3看出,mean-CCA的性能高于CCA,KCCA的性能也不是太好,而cluster-CCA和cluster-KCCA的性能明显优于其他算法。
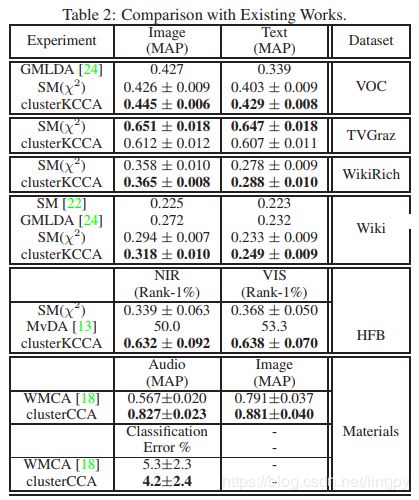
与现存的方法比较。其中 S M ( χ 2 ) SM(χ^2 ) SM(χ2)是 S M SM SM方法使用了 S V M SVM SVM作为分类器。
3.4 结论
将CCA和cluster-CCA核化后,可以将其应用范围扩展至非线性,将CCA改进至cluster- CCA后,可以改进CCA只能应用于所有数据必须成对对应的数据集的性能,即:拓宽了应用范围。当然,也是有一定弊端的,就是在大型数据集上使用时,计算量很大,因为它在计算协方差的时候对数据的数量呈平方的关系增长。
4 2014-On the Role of Correlation and Abstraction in Cross-Modal Multimedia Retrieval[5]
4.1 主要思想
本文实际上是对2010年论文[1]所提出方法的一个整合,使其更加完整。同样包括CM、SM、SCM算法。
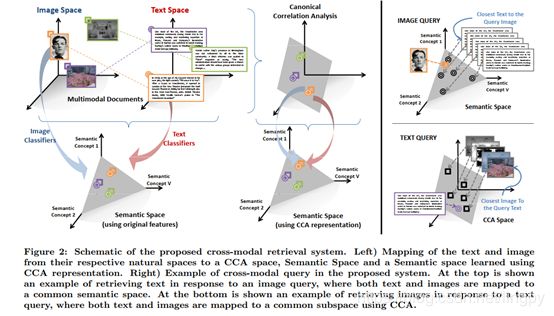
本文给出一个CCA方法如何学习子空间的原理图,笔者认为这个图很形象的解释了CM方法。
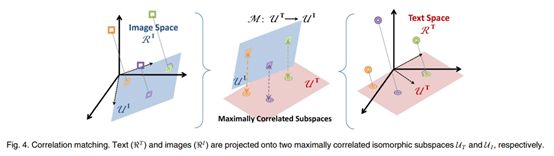
同样,本文也给出了SM方法原理图。 (同样很形象)
4.2 模型
大体上与[1]类似。相对于[1],本文对跨媒体检索方法做了一些分类,包括以下几个方面。
4.2.1 相关匹配(CM)
关于CM详见1.2.2。本文总结了4个部分,分别是线性子空间学习、非线性子空间学习、图像和文本投影以及相关匹配(最后两个部分见1.2.2)。
- 线性子空间学习。包括CFA(如下图)和CCA算法(见1.2.2)。
- 非线性子空间学习。主要指KCCA算法,详见2.2。
4.2.2 语义匹配(SM)
这一部分与1.2.3方法类似。不同之处是增加了另外两种分类器。
原1.2.3在求语义空间的映射矩阵时用到了逻辑回归算法。本文又增加了SVM算法和Boosting方法。其相关原理简单介绍如下。
SVM学习两个类之间最大边距的分离超平面,其优化函数如下:
min w , b , ξ 1 2 w ′ w + C ∑ i ξ i s . t . y i ( w ′ x i + b ) ≥ 1 − ξ i , ∀ i ξ i ≥ 0 , (1-9) \min_{w,b,\xi}\frac{1}{2}w'w+C\sum_i\xi_i \\ s.t.\ y_i(w'x_i+b) \geq 1-\xi_i,\forall i \ \xi_i \geq0, \tag{1-9} w,b,ξmin21w′w+Ci∑ξis.t. yi(w′xi+b)≥1−ξi,∀i ξi≥0,(1-9)
w w w和 b b b是超平面参数, y i y_i yi是类标签, x i x_i xi是输入特征向量, ξ i ξ_i ξi是松弛变量, C > 0 C>0 C>0是异常值(孤立点)的惩罚系数,
Boosting方法通过联合一系列弱学习器变为一个强规则学习器。详细描述自行百度or谷歌。
4.2.3 语义相关篇匹配(SCM)
见本文1.2.4。
4.3 实验
本文实验更加丰富,并加入了一些优化方法。
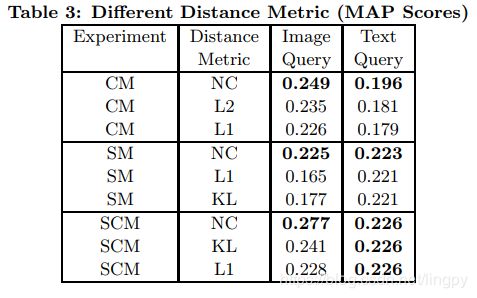
首先进行了使用不同距离度量方法的实验,包括Kullback-Leibler divergence(KL),l_1和l_2范数,normalized correlation (NC) 和 centered normalized correlation (NC_c)。实验结果表明NC_c性能最好,因此将使用NC_c作为实验的距离度量。
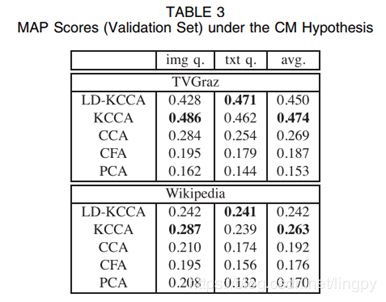
在进行CM实验时,加入了线性判别KCCA方法,最终结果表明KCCA和LD-KCCA性能较好。如下图。
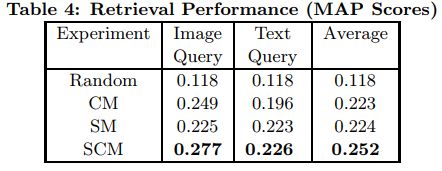
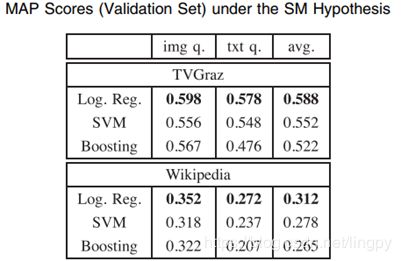
然后是SM实验。论文比较了3种分类器,结果表明逻辑回归分类器性能最好。如下图。
最后进行了整体的跨媒体检索实验,包括CM、SM、SCM和Baseline的对比实验。如图所示。
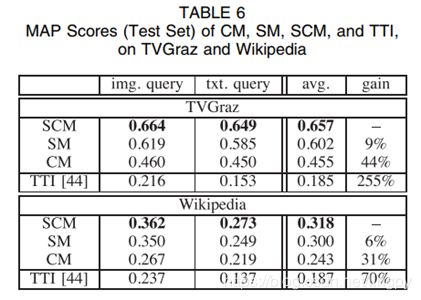
实验表明,SCM算法获得了最好的检索效果。
4.4 讨论
本文是[1]的扩充版,更加详细的介绍了CM、SM、SCM算法。
5 2015- Multi-Label Cross-modal Retrieval[6]
5.1 主要思想
本文提出多标签典型相关分析,以解决多标签注释的跨媒体检索问题。
常用的CCA方法由于简单性和高效率而广受欢迎,但它有几个缺点。最明显的缺点是CCA无法考虑高级的语义信息,比如数据的类标签。
本文提出的多标签典型相关分析(ml-CCA),可以利用多标签信息,同时学习两种模态的共同语义空间。此外也提出了fast ml-CCA,相比于ml-CCA,大大提高了效率。
5.2 模型
对于多标签数据集,不同模态之间存在自然的多对多对应关系,即来自一种模态的每个数据点与来自另一模态的若干其他数据点相关。如图5.1所示。
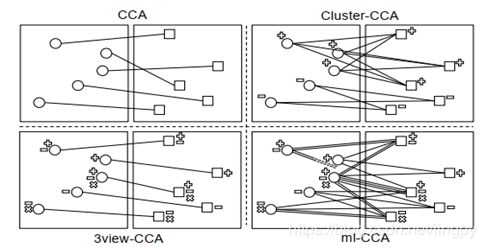
5.3 多标签典型相关分析算法(Multi-Label C anonical Correlation Analysis,ml-CCA)
见论文[6] 3.2节。
5.4 实验
略。
参考文献
[1] N. Rasiwasia et al., “A new approach to cross-modal multimedia retrieval,” in Proc. ACM Int. Conf.
Multimedia (ACM MM), 2010, pp. 251–260.
[2] G. Andrew, R. Arora, J. Bilmes, and K. Livescu, “Deep canonical correlation analysis,” in Proc. Int. Conf. Mach. Learn. (ICML), 2013, pp. 3408–3415.
[3] S. J. Hwang and K. Grauman, “Learning the relative importance of objects from tagged images for retrieval and cross-modal search,” Int. J. Comput. Vis., vol. 100, no. 2, pp. 134–153, 2012.
[4] N. Rasiwasia, D. Mahajan, V. Mahadevan, and G. Aggarwal, “Cluster canonical correlation analysis,” in Proc. Int. Conf. Artif. Intell. Statist. (AISTATS), 2014, pp. 823–831.
[5] J. C. Pereira et al., “On the role of correlation and abstraction in crossmodal multimedia retrieval,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 36, no. 3, pp. 521–535, Mar. 2014.
[6] V. Ranjan, N. Rasiwasia, and C. V. Jawahar, “Multi-label cross-modal retrieval,” in Proc. IEEE Int. Conf. Comput. Vis. (ICCV), Dec. 2015, pp. 4094–4102.