机器学习从零开始系列连载(五)——纯Python手写感知机模型
文章目录
- 感知机实现原理
- 感知机python代码实现
- 准备数据
- 取数据并且定义初始化与sign函数
- 训练结果可视化
- perceptron类封装
感知机是二类分类的线性分类模型,其输入为实例的特征向量,输出为实例的类别,取+1和-1二值。感知机对应于输入空间(特征空间)中将实例划分为正负两类的分离超平面,属于判别模型。感知机学习旨在求出将训练数据进行线性划分的分离超平面,为此,导入基于误分类的损失函数,利用梯度下降法对损失函数进行极小化,求得感知机模型。感知机学习算法简单并且容易实现,分为原始形式和对偶形式。

感知机实现原理
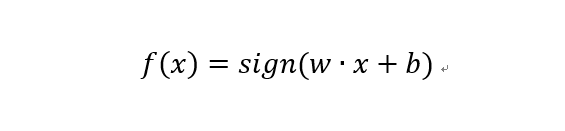
其中sign符号函数为:
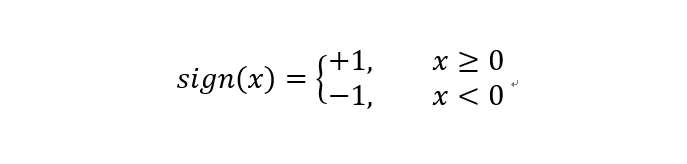 w和b为感知机模型参数,也是感知机要学习的东西。w和b构成的线性方程wx+b=0极为线性分离超平面。
w和b为感知机模型参数,也是感知机要学习的东西。w和b构成的线性方程wx+b=0极为线性分离超平面。
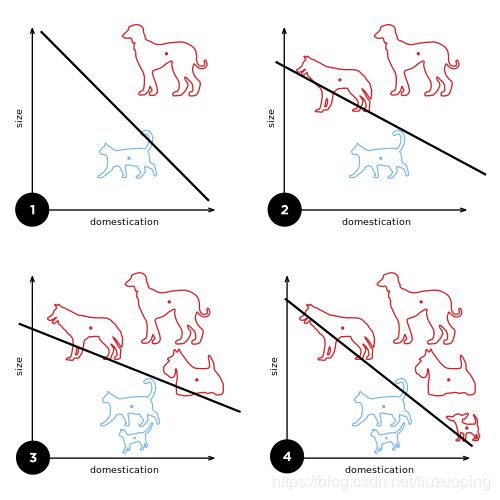
有且仅在数据线性可分的情况下,感知机才能奏效。感知机模型简单,但这也是其缺陷之一。所谓线性可分,也即对于任何输入和输出数据都存在某个线性超平面wx+b=0能够将数据集中的正实例点和负实例点完全正确的划分到超平面两侧,这样数据集就是线性可分的。 感知机的训练目标就是找到这个线性可分的超平面。为此,定义感知机模型损失函数如下:
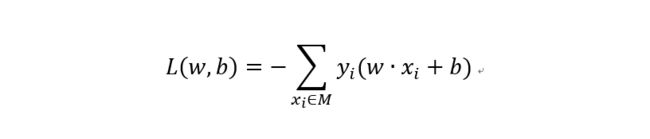 要优化这个损失函数,可采用梯度下降法对参数进行更新以最小化损失函数。计算损失函数关于参数w和b的梯度如下:
要优化这个损失函数,可采用梯度下降法对参数进行更新以最小化损失函数。计算损失函数关于参数w和b的梯度如下:
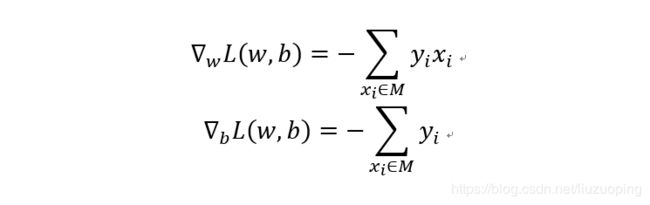
感知机python代码实现
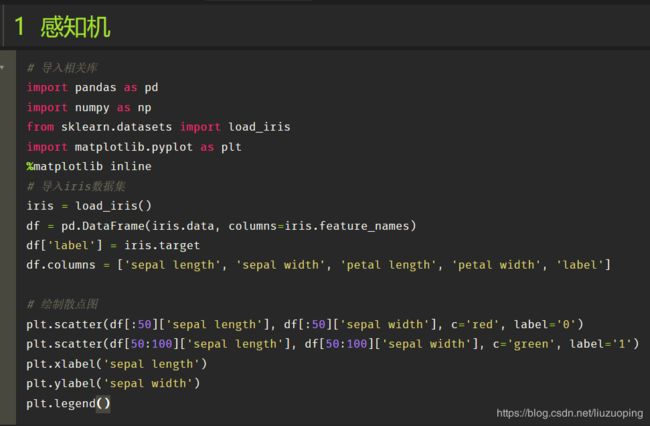
完整的感知机算法包括参数初始化、模型主体、参数优化等部分,我们便可以按照这个思路来实现感知机算法。在正式写模型之前,我们先用sklearn的iris_data准备一下示例数据。
准备数据
取数据并且定义初始化与sign函数
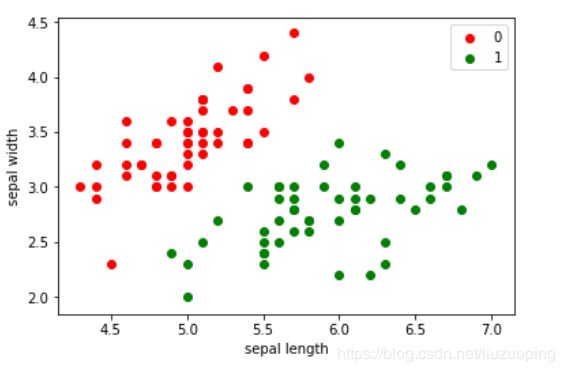
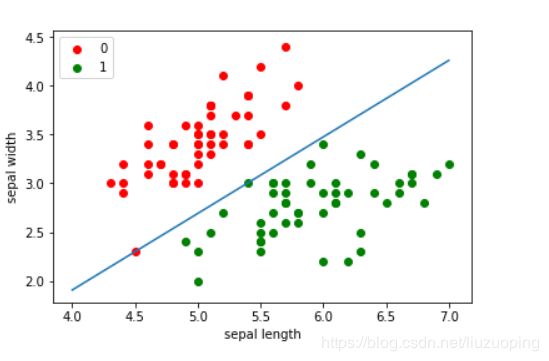
训练结果可视化
perceptron类封装
class Perceptron:
def __init__(self):
pass
def sign(self, x, w, b):
return np.dot(x, w) + b
def train(self, X_train, y_train, learning_rate):
# 参数初始化
w, b = self.initilize_with_zeros(X_train.shape[1])
# 初始化误分类
is_wrong = False
while not is_wrong:
wrong_count = 0
for i in range(len(X_train)):
X = X_train[i]
y = y_train[i]
# 如果存在误分类点
# 更新参数
# 直到没有误分类点
if y * self.sign(X, w, b) <= 0:
w = w + learning_rate*np.dot(y, X)
b = b + learning_rate*y
wrong_count += 1
if wrong_count == 0:
is_wrong = True
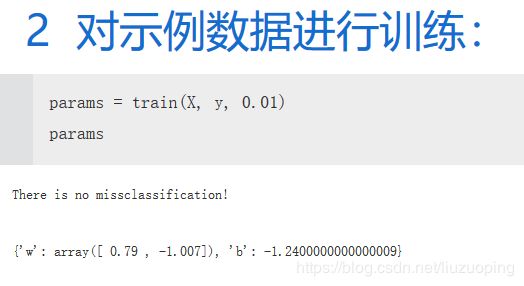
print('There is no missclassification!')
# 保存更新后的参数
params = {
'w': w,
'b': b
}
return params