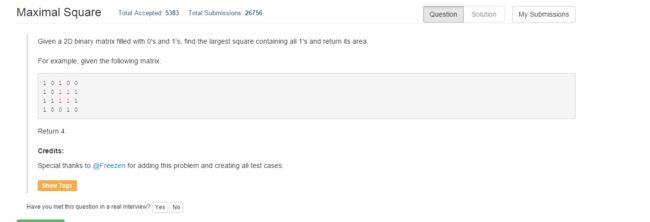
Question:
My code:
public class Solution {
private int width;
private int height;
public int maximalSquare(char[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0)
return 0;
width = matrix[0].length;
height = matrix.length;
int max = 0;
for (int i = 0; i < height; i++) {
if (max < matrix[i][0] - '0') {
max = 1;
break;
}
}
for (int i = 0; i < width; i++) {
if (max < matrix[0][i] - '0') {
max = 1;
break;
}
}
for (int i = 1; i < height; i++) {
for (int j = 1; j < width; j++) {
if (matrix[i][j] == '1')
matrix[i][j] = (char)(Math.min(matrix[i][j - 1] - '0', Math.min(matrix[i - 1][j] - '0', matrix[i - 1][j - 1] - '0')) + 1 + '0');
}
}
for (int i = 0; i < height; i++) {
for (int j = 0; j < width; j++) {
if (max < matrix[i][j] - '0')
max = matrix[i][j] - '0';
}
}
return max * max;
}
public static void main(String[] args) {
char[][] a = new char[5][4];
a[0][0] = '0';
a[0][1] = '0';
a[0][2] = '0';
a[0][3] = '1';
a[1][0] = '1';
a[1][1] = '1';
a[1][2] = '0';
a[1][3] = '1';
a[2][0] = '1';
a[2][1] = '1';
a[2][2] = '1';
a[2][3] = '1';
a[3][0] = '0';
a[3][1] = '1';
a[3][2] = '1';
a[3][3] = '1';
a[4][0] = '0';
a[4][1] = '1';
a[4][2] = '1';
a[4][3] = '1';
Solution test = new Solution();
System.out.println(test.maximalSquare(a));
}
}
My test result:
这次作业也是挺难的。然后我自己做出来的那个版本跑的时间过长,测试过不了。后来看了别人的提示,发现这道题目有两种解法,我重点研究了第二种解法。用动态规划来求解。
我的方法是。从最大的正方形开始找。如果不是,则把这个正方形分成四个子次大正方形,递归下去进行判断,直到找到最大的。但其中存在大量的重复,所以时间上过长是可以理解的。
展示下我写的代码,愚蠢的代码:
public class Solution {
private int width;
private int height;
public int maximalSquare(char[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0)
return 0;
width = matrix[0].length;
height = matrix.length;
int max = 0;
if (width > height) {
for (int i = 0; i <= width - height; i++) {
if (max < getMax(0, i, height, matrix))
max = getMax(0, i, height, matrix);
}
}
else {
for (int i = 0; i <= height - width; i++) {
if (max < getMax(i, 0, width, matrix))
max = getMax(i, 0, width, matrix);
}
}
return max;
}
private int getMax(int x, int y, int lengthOfSide, char[][] matrix) {
if (lengthOfSide <= 0 || x < 0 || x >= height || y < 0 || y >= width)
return 0;
boolean isSquare = true;
for (int i = x; i < x + lengthOfSide; i++) {
for (int j = y; j < y + lengthOfSide; j++) {
if (matrix[i][j] != '1') {
isSquare = false;
break;
}
}
if (!isSquare)
break;
}
if (isSquare)
return lengthOfSide * lengthOfSide;
else {
int a = getMax(x, y, lengthOfSide - 1, matrix);
int b = getMax(x, y + 1, lengthOfSide - 1, matrix);
int c = getMax(x + 1, y, lengthOfSide - 1, matrix);
int d = getMax(x + 1, y + 1, lengthOfSide - 1, matrix);
return Math.max(Math.max(a, b), Math.max(c, d));
}
}
public static void main(String[] args) {
char[][] a = new char[5][4];
a[0][0] = '0';
a[0][1] = '0';
a[0][2] = '0';
a[0][3] = '1';
a[1][0] = '1';
a[1][1] = '1';
a[1][2] = '0';
a[1][3] = '1';
a[2][0] = '1';
a[2][1] = '1';
a[2][2] = '1';
a[2][3] = '1';
a[3][0] = '0';
a[3][1] = '1';
a[3][2] = '1';
a[3][3] = '1';
a[4][0] = '0';
a[4][1] = '1';
a[4][2] = '1';
a[4][3] = '1';
Solution test = new Solution();
System.out.println(test.maximalSquare(a));
}
}
DP的思路是,从11的小正方形开始,再到 22 - 33-.....
直到最后。然后遍历整个矩阵,找出最大的那个。
判断某点是否是正方形一部分时,如果该点值是1,则其具有构成正方形的可能。就假设该点是正方形的最右侧点。然后检查其左边,上边,左上方,三个点,即。
(i-1,j) (i,j-1) (i-1,j-1)
取他们的最小值。如果三者有0,则最小值是0.然后该点的值继续保持1.表示他构成的正方形边长是一。如果三者都等于2.那么该点值就等于3.
因为那三者等于2,表示各自都是一个22正方形的右下方点。那么,再加上这个值为一的点,他们就能构成一个3*3的正方形。而该点恰是右下方点,值为3,表示其边长为3.
如此遍历大部分点。当遍历结束后,再次遍历整个矩阵。最大值即为最大边长。
然后展示下采用直方图那道题目 Largest Rectangle in Histogram 思想的截图代码:
其实和那道题目代码基本一致了。(搬运某个网友的代码)
相关链接:
http://blog.csdn.net/gldemo/article/details/46665019
public class Solution {
public int maximalRectangle(char[][] matrix) {
//边界处理
if(matrix == null || matrix.length == 0 || matrix[0].length == 0){
return 0;
}
int rLen = matrix.length;//row行数
int cLen = matrix[0].length;//column列数
int[] height = new int[cLen+1];
height[cLen] = 0;
int maxArea = 0;
for(int j=0;j indexStack = new Stack();
for(int i=0;i= height[indexStack.peek()]) {
indexStack.push(i);
} else {
while(!indexStack.empty() && height[i] < height[indexStack.peek()]) {
int top = indexStack.pop();
int curArea = height[top]*(indexStack.empty()?i:(i-indexStack.peek()-1));//i-indexStack.peek()-1也可以写成 i-top
if(curArea>maxArea){
maxArea = curArea;
}
}
indexStack.push(i);
}
}
}
return maxArea;
}
}
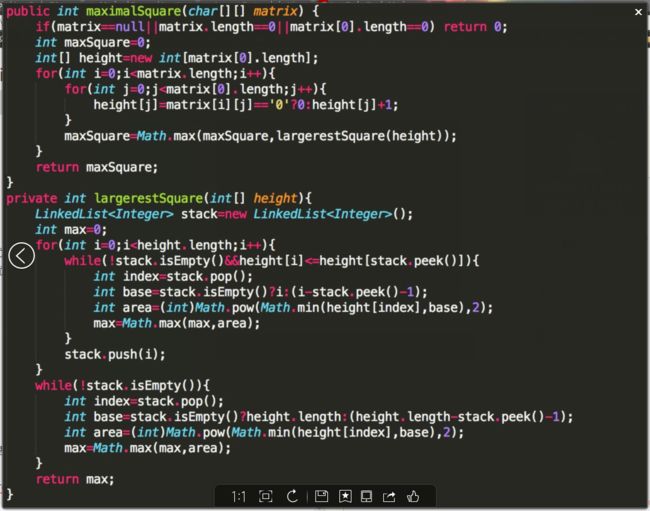
额。。。刚刚测试了下这个代码,发现是错的。因为他求的是矩形面积,和正方形还是有一些区别的,其实再稍微改下就差不多了。现在没精力了。贴一张正确代码的截图,也是别人的。
**
总结:没什么好总结的。。。感觉这就是一种思路。碰过了,就熟悉了。
**
希望,我们,一切顺利。希望你,平安,幸福,健康。
Anyway, Good luck, Richardo!
My code:
public class Solution {
public int maximalSquare(char[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return 0;
}
int row = matrix.length;
int col = matrix[0].length;
int[][] dp = new int[row][col];
for (int i = 0; i < col; i++) {
if (matrix[0][i] == '1') {
dp[0][i] = 1;
}
}
for (int i = 0; i < row; i++) {
if (matrix[i][0] == '1') {
dp[i][0] = 1;
}
}
for (int i = 1; i < row; i++) {
for (int j = 1; j < col; j++) {
if (matrix[i][j] == '1') {
int base = Math.min(dp[i - 1][j], Math.min(dp[i][j - 1], dp[i - 1][j - 1]));
if (base == 0) {
dp[i][j] = 1;
}
else {
dp[i][j] = base + 1;
}
}
}
}
int max = 0;
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
max = Math.max(max, dp[i][j]);
}
}
return max * max;
}
}
思路还是记得的。跟 triangle里面求最小路径差不多的思想。
Anyway, Good luck, Richardo! -- 08/18/2016