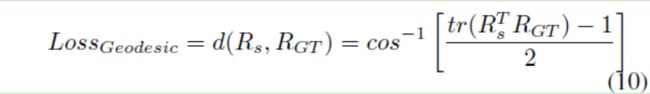【配准】2019医学图像配准中的深度学习综述论文解读(1)
这篇博文我转载到了知乎专栏上并进行了参考文献的扩充,可供参阅。
https://zhuanlan.zhihu.com/p/92032320
论文:Deep Learning in Medical Image Registration: A Survey
阅读中主要关注点:配准的各个流派大致的思路,比较有意思的想法,刚性配准的网络架构与目标函数
一、研究情况梗概
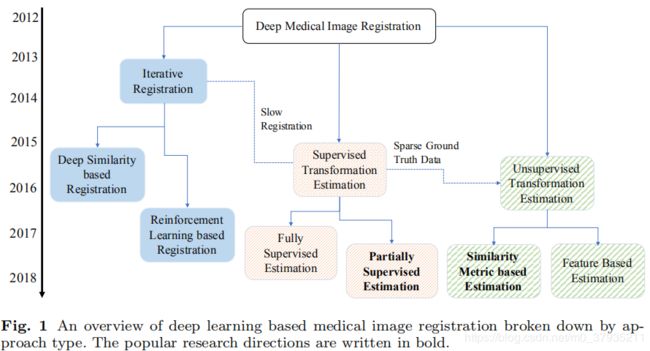
目前采用深度学习进行医学影像配准的方法大致可以分为三类:
- 深度迭代配准的方法。不断迭代优化相似性测度来实现配准。具体可以分为两种:传统配准方法的拓展,通常是采用深度学习方法提取特征描述子,再用传统方法迭代优化目标函数;另一种是采用深度强化学习。
- 采用监督学习或弱监督实现一步配准。监督学习的话金标准的制作是个较大的问题。因此目前弱监督是研究热点。
- 采用非监督学习实现一步配准。非监督一块目前基于相似性测度进行自监督学习是研究热点。但对于多模态配准问题,相似性测度的选择是一大挑战。
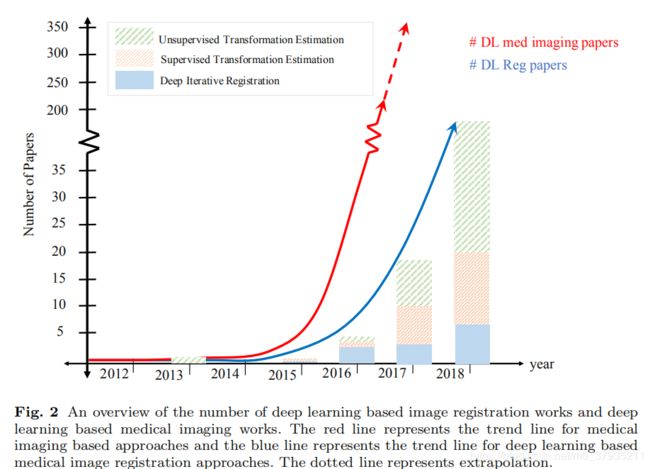
研究情况的发展趋势可以看这张图
差不多2016年才渐渐出现采用深度学习进行配准的论文。早期的研究业也以深度迭代学习的方法居多。由于对配准速度的需求,基于深度学习进行一步配准的方法开始出现,比如采用类似Unet的网络来学习形变场。这种方法需要真实的形变场作为金标准,而真实形变场很难得到,因此刺激了非监督学习方法的出现。该种方法面对的一大挑战是相似性测度的选择。最近的很多研究都是为了解决这一问题,比如采用基于信息论的相似性测度,比如弱监督方法,比如GAN的应用。
当前用于配准的深度学习模型主要有四类:
- 卷积神经网络。最常见,最普遍。
- 循环神经网络。目前的研究较少,文章中列举的上百篇参考文献中不超过5篇。但当前采用循环神经网络用于关键点检测的论文频繁出现,对配准可能有一定启发。
- 强化学习。已有的研究都是深度迭代学习的。差点跳过的坑不敢再跳了,这部分略过。
- 生成对抗网络。目前已有一定数量的论文出现,可能是下一步的研究热点。
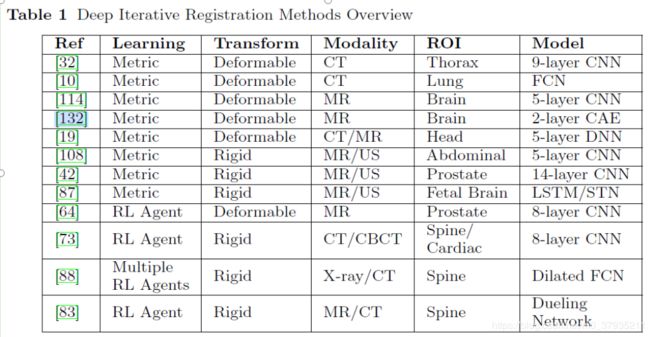
二、深度迭代学习
这是最早的将深度学习应用于医学图像配准的研究。我们先来看一下这之前的传统的配准方法。
I1,I2是待配准两副图像提取特征后得到的特征空间,也可以将原图所有像素作为特征空间,此时的I1,I2就是待配准的两张图像;我们选择一个合适的变换模型(比如仿射变换),将I2变换后得到I2*,选择合适的相似性测度计算I2*和I1的相似度,我们希望这个相似度越小越好,因此需要采用一种优化策略(或者说优化算法)来迭代优化目标函数相似度,找到合适的几何变换参数使得相似度最小。一些人工设计的相似性测度经常被使用,比如平方和误差(SSD),互相关函数(CC),互信息(MI),标准互相关函数(NCC),标准互信息(NMI)。
常见的配准方法有两种
- 基于体素的 上图的I1,I2替换为就是原图。难点在于相似性测度的设计。
- 基于特征点的。具体做法是提取特征,匹配特征,通过拟合或插值算法得到形变场。这种做法往往不涉及相似性测度,但特征的选择和匹配是难点。
那么深度学习是如何在传统的方法上进行改进的呢?
我们来看最早的文献的做法([132,133])
这篇论文提出了一种非监督的特征提取方法用于配准任务。它的想法是采用stack autoencode(SAE)网络来非监督学习特征,从而得到泛化能力更强更具有特征性的特征。
这种特征学习方法可以不仅可以融入到传统的基于特征点的配准方法中,也可以融入基于灰度的配准方法中。下面看一下融入HARMMER算法(基于特征点类型)的具体做法。
上图是SAE网络,蓝色的部分就是我们想要的特征向量。我们训练该网络希望该网络的输出ym与网络输入xm尽量相似。
首先是选择大量的关键点得到patch块来训练这个SAE网络。
然后就是配准两张图像:选择关键点,提取特征向量并匹配关键点,插值得到密集形变场,重复直到所有点都曾被选为关键点。
总而言之,该种做法的本质依然是传统的基于迭代优化的配准方法,只是不再采用传统的特征描述子,而是使用深度学习的做法来学习每个关键点的特征描述子来指导关键点的匹配。最近有研究表明,在单模态的情况,深度学习学到的特征描述子并不一定比手工设计的特征描述子效果好,通常两者的结合能取得更好的效果,因为往往前者可以是后者的一个信息补充。
刚刚提到的最早的那篇论文是用深度学习来学习特征描述子。关键点的匹配,形变模型的插值等方法依然是传统的方法。
还有一个研究方向是用深度学习来学习两个patch块的相似性测度从而衡量两个patch对应的特征点是否匹配。该种方法的思路是训练一个二分类的分类器来衡量两个点的匹配程度。可以看下图,输入两个patch块拉长的向量的串联,输出01或10代表匹配或者不匹配。通过这种监督学习的方式来实现相似性测度的学习。多用于多模态图像的配准。
三、带监督的形变场估计
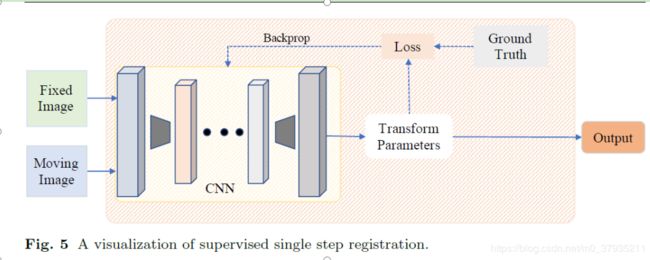
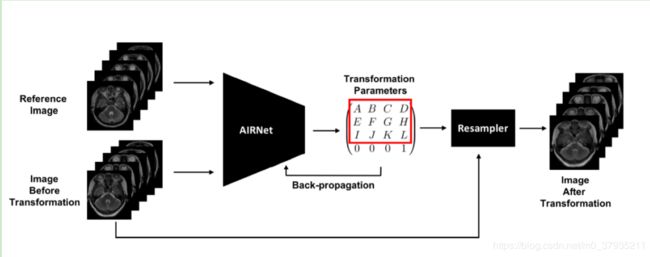
迭代学习的一大缺点就是速度很慢,无法满足实时配准的需求。因此通过神经网络直接估计形变场的方法开始出现。可以看下面这张图。
我们来看具体的做法,先看最简单粗暴的一些做法——采用全监督的形式进行刚性配准。
最早的论文[89,90]:把配准的问题当做回归问题解决,从图片中回归出变换参数。
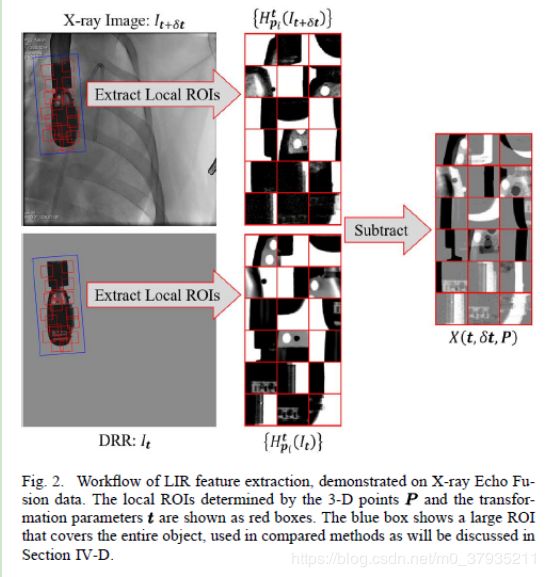
首先:提取出局部图像残差特征。
然后通过一个CNN回归出仿射矩阵的参数残差(下下图公式6)
贴一下相关公式:
需要说明的是,想要从配准的图像中直接回归中变换参数是很艰难的,作者为了简化这一问题采用了很多策略。如局部网络残差的计算,参数空间的划分。
2018年有一篇论文[16]采用的配准方法是利用一个回归网络直接从原图中回归出仿射矩阵的12个参数(三维图像配准)。目标函数就是这12个参数与金标准的MSE。这是目前更为常见的做法。
由于从现有的待配准的图像对中难以得到金标准,所以作者采用了自己生成的数据作为训练数据。我认为这篇论文比较有价值的有两点。一是网络架构:
它的网络分为编码网络和回归网络两部分。编码网络采用了DenseNet的模块来搭建,并采用了权值共享的方法来获得参考图像与浮动图像匹配的特征,同时减少参数数量。我们可以看到它的编码网络网络深度还挺深的,有70层(输入图像30*320*320),作者并没有提到如何选择网络的深度,但我个人认为可能是较浅的网络无法提取出复杂的特征用于回归。另外,这个回归网络层数也较深,一层一层神经元数量逐步减少,最终回归出12个参数,而不是从8192个神经元直接回归出12个。
二就是它数据生成的方法。对于配准问题数据量不够是个很让人头痛的问题。而现在很常见的一种数据增强方法就是自己生成待配准的数据。本文就是随机生成仿射变换矩阵,根据这个由参考图形生成浮动图像,变换矩阵就是金标准。
类似的论文还有[116],这篇论文是采用神经网络回归出MR slice刚性配准的三个参数,θ,tx,ty。这篇论文比较了两个网络架构作为回归网络的效果:CNN和FCN,区别是最后几层是全连接还是卷积,从实验结果看这两个区别不大。论文中提到设计网络时最好不要用最大池化层,因为最大池化层具有局部平移不变性,对平移参数的估计存在影响,这一点曾有论文讨论过该问题,我记得结论是最大池化是可以用的。论文还讨论了引入可逆性对配准结果的影响,实现结果发现引进可逆性之后配准效果并没有提升,作者没有分析原因。(我觉得该论文参考价值不太大。)
【106】这篇论文同样采用CNN回归出刚性配准的参数。我认为这篇论文的亮点在于geodesic loss的应用。我们现在看一下它的方法,再说这个loss。
整体的配准思路如下图
输入图片,提取特征,然后根据特征回归出变换参数。目前我看到的刚性配准的论文大多都是这个思路,通常能够创新的也就以下几点:
- 输入 如[89,90,143]先提取了局部特征再输入网络进行进一步的特征提取和回归。这样做能够降低网络设计和训练的难度,但不是端到端的学习,局部特征提取方法通常采用传统的算法,相对繁琐。个人认为并不是目前主流的研究方向。
- 网络架构 目前看到的网络架构通常都是借用的分类或者分割的网络,常见的就是FCN还有ResNet,也有很多是自己搭建的简单的网络序列,除了STN(Spatial Transformer Networks )目前尚没有看到较为新颖的网络模块的设计。较多的创新还是集中在配准思路的设计上,比如把配准分为两步,训练一个网络进行粗配准,另一个网络进行精细配准。(可能是我目前阅读的论文量还比较少,见识浅薄)
- 目标函数 监督学习部分目标函数多是MSE,而非监督,弱监督在这方面的改动就比较多了。而本文的创新点也在这部分。
上图是二维切片做三维姿态估计的网络架构。作者尝试了VGG16,ResNet18,DenseNet,发现ResNet18效果最好。回归部分分为两个部分,上面的支路回归出三维旋转变换的3个参数,其中pi tanh是用来限制旋转参数范围在[-pi,pi]。下面的支路回归出一个标量,代表位置。Loss采用的MSE
上图是三维图像块做姿态估计的网络架构。分为两步,第一步是估计出三维图像块的旋转角度(相对canonical坐标系),可视为粗配准,loss采用的常见的MSE。第二步是精细配准,将上一步得到的粗配准后的图像和参考图像输入网络,得到最终的变换参数(3个旋转参数,3个平移参数)。平移参数的loss依然是MSE,旋转参数的是geodesic loss。由于这篇论文的任务是姿态估计,并不是任意两张图像的配准,所以网络的输入一般是单幅图像,这里第二步输入了参考图像,这里的参考图像是通过梯度中心匹配算法计算出来的。
这篇论文配准的思路大体就是这样,并没有看到太吸引人的突破。但这篇论文发表在TMI上应该还是有其道理的。比如geodesic loss的应用。作者说MSE是一个凸函数,能很好地收缩学习过程中的搜索空间,解决常见的陷入局部最优问题。但是MSE并不能准确地表示两个旋转矢量之间的距离,所以为了提高准确度,作者采用了测地距离,也就是单位球面上两个点之间的最短距离。
这篇论文实验部分看着挺好的,有时间再细读。
监督学习的方法问题在于配准的质量对金标准的依赖大,而金标准的质量又依赖于制作者的专业程度;此外金标准的获取也是一个难题,尽管可以通过自己生成训练数据来解决这些问题,但是如何保证生成的数据和临床数据足够相似也是一个问题。
下一篇博文:解读双监督,弱监督和非监督部分。