机器学习 -- 支持向量机SVM（Ⅳ sklearn中的SVM）

使用SVM算法和使用kNN一样，要做数据标准化处理（涉及距离，需要统一量纲）。

（1）导入所需的模块和包

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

（2）加载并提取部分数据集

iris = datasets.load_iris()

X = iris.data
y = iris.target

X = X[y < 2, :2]
y = y[y < 2]

（3）绘制出提取的数据集的点

plt.scatter(X[y == 0, 0], X[y == 0, 1], color='r')
plt.scatter(X[y == 1, 0], X[y == 1, 1], color='b')
plt.show()

（4）数据集的归一化处理

from sklearn.preprocessing import StandardScaler

standardScaler = StandardScaler()
standardScaler.fit(X)
X_standard = standardScaler.transform(X)

（5）导入linearSVC线性分类支持向量机

from sklearn.svm import LinearSVC

（6）绘制决策边界的函数

def plot_decision_boundary(model, axis):
       x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100))
    )
    x_new = np.c_[x0.ravel(), x1.ravel()]
    
    y_predict = model.predict(x_new).reshape(x0.shape)
 
    from matplotlib.colors import ListedColormap
    
    custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])
    
    plt.contourf(x0,x1,y_predict, linewidth=5, cmap=custom_cmap)

（7）实例化linearSVC线性分类支持向量机对象并绘制图像

C越大，容错空间越小；C越小，容错空间越大。

① C取较大的数值时：

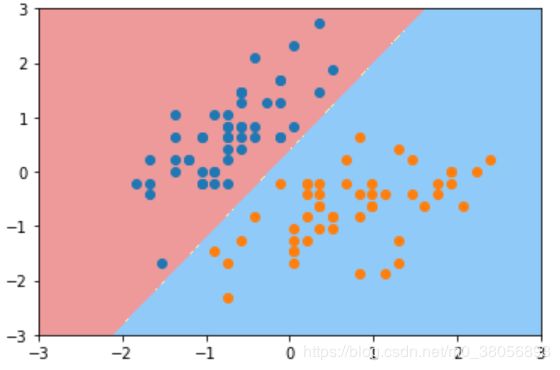
svc = LinearSVC(C=1e9)
svc.fit(X_standard, y)

plot_decision_boundary(svc, axis=[-3, 3, -3, 3])
plt.scatter(X_standard[y == 0, 0], X_standard[y == 0, 1])
plt.scatter(X_standard[y == 1, 0], X_standard[y == 1, 1])
plt.show()

② C取较小的数值时：

svc2 = LinearSVC(C=0.01)
svc2.fit(X_standard, y)

plot_decision_boundary(svc2, axis=[-3, 3, -3, 3])
plt.scatter(X_standard[y == 0, 0], X_standard[y == 0, 1])
plt.scatter(X_standard[y == 1, 0], X_standard[y == 1, 1])
plt.show()

（8）定义一个绘制svc决策边界的函数

def plot_svc_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100))
    )
    x_new = np.c_[x0.ravel(), x1.ravel()]
    
    y_predict = model.predict(x_new).reshape(x0.shape)
 
    from matplotlib.colors import ListedColormap
    
    custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])
    
    plt.contourf(x0,x1,y_predict, linewidth=5, cmap=custom_cmap)
    
    w = model.coef_[0]
    b = model.intercept_[0]
    
    # 决策边界直线方程： w0 * x0 + w1 * x1 + b = 0
    # => x1 = -b / w1 - w0 * x0 / w1
    plot_x = np.linspace(axis[0], axis[1], 200)
    up_y = -b/w[1] - w[0]/w[1] * plot_x + 1/w[1] 
    down_y = -b/w[1] - w[0]/w[1] * plot_x - 1/w[1] 
    
    # 过滤
    up_index = (up_y >= axis[2]) & (up_y <= axis[3])
    down_index = (down_y >= axis[2]) & (down_y <= axis[3])
    
    plt.plot(plot_x[up_index], up_y[up_index], color='black')
    plt.plot(plot_x[down_index], down_y[down_index], color='black')

（9）绘制图像，观察svc1和svc2区别

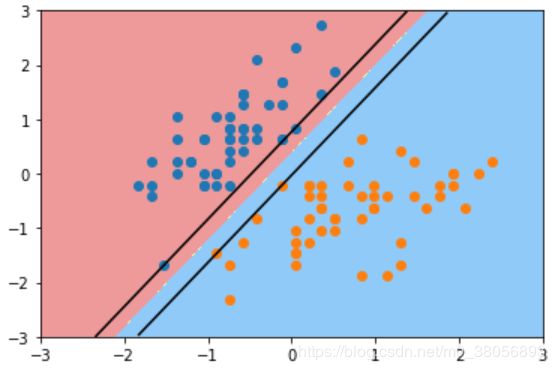
① svc1

plot_svc_decision_boundary(svc, axis=[-3, 3, -3, 3])
plt.scatter(X_standard[y == 0, 0], X_standard[y == 0, 1])
plt.scatter(X_standard[y == 1, 0], X_standard[y == 1, 1])
plt.show()

 

② svc2

plot_svc_decision_boundary(svc2, axis=[-3, 3, -3, 3])
plt.scatter(X_standard[y == 0, 0], X_standard[y == 0, 1])
plt.scatter(X_standard[y == 1, 0], X_standard[y == 1, 1])
plt.show()