运筹优化学习08：Repairing MIP infeasibility through local branching

寻找一般整数规划问题的可行解是一个比较困难的事情， feasibility pump和local branching方法的提出，为寻找MIP的可行解提供了新的思路，feasibility pump方法可以较低的成本提供局部分支过程的（不一定可行）初始解。在单纯形法中，通过引入人工变量求解增广模型，之后在迭代循环使人工变量的值趋于0，以获取问题的可行解。我们的方法也可以启发式的寻找最小基数约束集，将不可行的MIP转化为可行的MIP。

在实际的应用场景下，找到好的可行方案是商业发展的主要关注，局部搜索通常从一个初始的可行解出发，对其进行迭代改进，从而使算法终止于一个稳定的值。然而，有时找到一个初始解往往是比较困难且不必要的，因为可以通过修复策略使初始解变的可行并最终得到改进。基于上述分析，本文介绍求解MIP的 feasibility pump和local branching方法，这两种方法最初的设计理念就是为了寻找初始和改进初始可行解。

1 引言

1.1 基础模型

为了寻找到要研究问题的可行解决方案，我们首先定义包含0-1变量的MIP模型：

模型变量说明：

参数	描述
，	输入矩阵
	维度为m的向量
	维度为n的向量
	可分解为三个子集,分别表示0-1变量、整数变量和连续变量索引集

注意：

• 我们在这里假设存在0-1变量集，因为局部分支启发式算法需要基于这一假设。此外，也可以消除这一约束拓展我们的方法。
• 对于约束集(3)虽然呈现出不等式形式，但也包含了等式约束；可令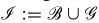表示所有的整数变量集合

 1.2 方法回顾：

• Fischetti提出所谓的局部分支启发时方法，来提升给定可行解的质量；【Fischetti M, LodiA. Local branching. Mathematical Programming 2003;98:23–47】
• Danna提出RINS启发式方法，需要一个初始可行解，但这对于一些MIP是比较困难的。【 Danna E, Rothberg E, Le Pape C. Exploring relaxation induced neighborhoods to improve MIP solutions. Mathematical Programming. 2005;102:71–90.】
•  Fischetti提出使用feasibility pump方法通过一系列巧妙的操作来发现MIP的可行或近似可行的解决方案。【Fischetti M, Glover F, LodiA. The feasibility pump. Mathematical Programming 2005;104:91–104.】

1.3 我们的工作

计算和分析了原始LB方法的简单变体，允许接受不可行的参考解，如使用FP返回的解；我们从FP以极小的计算成本提供的几乎可行的参考解出发，对每一个违反约束的MIP模型的约束通过以下三种形式进行放松：引入基于约束本身的人工连续变量、引入二进制人工变量；设置在必须使用人工变量才能满足的情况下将二进制变量设置为1的约束。最后目标函数被替换为类似于单纯形法第一阶段的二进制变量求和的形式。对于放松之后的模型，具有满足约束的可行初始解，其约束数目与违背初始约束的数目是一致的。我们使用标准的LB框架，减少目标函数的值，即不可行解的数目；对于初始问题，不可行解的数目为0时，便得到了它的可行解。尽管对于每一个违反的约束，连续性变量就足够了，但是LB使用二进制变量，则显示了更好的效果。

此外，我们的方法还产生了一个小的基数约束集，将其松弛可将不可行的MIP转化为可行的MIP，这对与分析不可行的MIP非常重要；换言之，可将其视为修复不可行MIP模型的工具，而不仅是修复不可行MIP解决方案的一种启发式方法，其思想与通常研究的寻找LP最大或最小子问题的可行解的理念是一致的。

2 局部分支和可行性泵方法

2.1 局部分支(Local Branching, LB)

基本原理如下：

对于问题给定一个可行的参考解，我们的目标是寻找距离并不太远的改进解。

令表示的二进制支持集，对于给定的正整数，定义的邻域为问题满足邻域分支约束的可行解：

左侧的两项分别为从1-0或0-1的二进制变量的翻转值；顾名思义，局部分支约束7可以用作问题P方案枚举的分支条件。实质上，若给定，与当前分支节点相关联的解空间做如下分解：

这里的邻域大小k应足够的小以保证在较短的时间内获得优化解，还应足够的大以保证能顾囊括比更好的解。

Fischetti(2003)的通过控制一个简单的外部分支框架，使用通用的MIP求解器作为一个黑箱工具来在子空间内搜索更合适的解，这个过程包含着著名的局部搜索元启发式算法理念，但是得到了包含邻域约束的MIP的局部分支约束(7)，这可以保证算法在一个更完美的框架下被开展实施。在MIP求解器中，通常采用的是精确求解算法策略，尽管LB算法是为了改进MIP求解器而做出的启发式行为。他利用战略级分支定义解的邻域，并在战术级层面上利用MIP求解器进行更优解探索。这一过程可视为一个两级分支策略，既能在早期对现有解进行更新，也能在计算的早期产生改进的解决方案。Fischetti(2003,2006)的研究结论表明，LB方法具有良好的性能，Hansen(2006)也采用变邻域搜索元启发式方法证明了这一点。

 Hansen P, Mladenovíc N, Urosevíc D. Variable neighborhood search and local branching. Computers and Operations Research 2006;33:3034–45.

 Fischetti M, Polo C, Scantamburlo M. A local branching heuristic for mixed-integer programs with 2-level variables. Networks 2004;44:61–72.

2.2 可行泵

表示与给定MIP的LP松弛相关的凸多面体，不失一般性，我们假设包含具有界限的变量集，这里对于所有的都有和。

3 从不可行解开始的局部分支方法

局部分支技术并不严格要求从一个可行解开始，也即一个部分可行的解也可以。通过以合适的方式对模型进行放松，我们有可能将一个不可行解通过局部分支启发式骑术使其逐步变更为可行解。

一种常用的实现方式为，为不可行解中的违反约束添加一个连续的人工变量，使用M对其进行惩罚，这种方法已经被测试是有效的，但是在实际应用中确定M是比较困难的。对于MIPLIB中的许多算例，他们的目标函数值是非常大的，使用M并不能体现出不可行解比可行解差的情形。LB采用了如下组合优化框架：