相关链接
在暑假里面粗略地学习了一下CS231n的课程,个人感觉非常有收获,对于入门深度学习中的计算机视觉特别有效。现在想通过写博客这种方式,来再一遍地找漏巩固。下面是一些课程的官方链接:
| 网页 | 说明 |
|---|---|
| 课程主页 | 这个网页上还有2015到2018的过去几年的课程链接 |
| 课程笔记 | 有三次作业链接和三个模块的笔记、教程 |
| 详细的教学大纲 | 有对应视频课程的slides,拓展阅读,也包含笔记 |
当然这么好的课程国内肯定会有翻译的:
| 网页 | 说明 |
|---|---|
| 9篇课程知识详解笔记的翻译 | 只是对应的是2016冬季课程的 |
| 课程视频 | B站上的中英字幕的,网易云课堂截止本博客发出仍处于下架状态 |
| 作业1代码 | 我写的针对2019春季课程的参考代码 |
Assignment 1
这个是作业链接及说明:Assignment #1: Image Classification, kNN, SVM, Softmax, Neural Network,里面需要用Ipython Notebook(关于这个工具的教程可看这里)的形式完成5个小问题:knn.ipynb、svm.ipynb、softmax.ipynb、two_layer_net.ipynb、features.ipynb(没有基础,想看一下python和numpy的简易教程的可以看这里),从这些问题文件的命名就可以大致看出要完成什么。想完成assignment1,主要要阅读完这两个笔记:
- Image Classification: Data-driven Approach, k-Nearest Neighbor, train/val/test splits
- Linear classification: Support Vector Machine, Softmax
KNN
这里有一点我写的关于KNN的理解,KNN其实是Nearest Neighbor的拓展,在训练阶段只做数据的记录,在预测的时候,通过某种指标来求得与输入的要预测图片“距离”最近的一张图片,将它的标签作为预测结果。KNN就是求出“距离”最近的K张图片,投票选出多数的标签作为结果。其中最好的K值由交叉验证决定(Cross-validation)。
knn.ipynb里面需要写三种计算”距离“的函数,还有一个预测函数:
用两个循环的很好理解,不用多解释
def compute_distances_two_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a nested loop over both the training data and the
test data.
Inputs:
- X: A numpy array of shape (num_test, D) containing test data.
Returns:
- dists: A numpy array of shape (num_test, num_train) where dists[i, j]
is the Euclidean distance between the ith test point and the jth training
point.
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
for i in range(num_test):
for j in range(num_train):
dists[i,j] = np.sqrt(np.sum((X[i,:] - self.X_train[j,:]) ** 2))
return dists
用一个循环的也很好理解:
def compute_distances_one_loop(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a single loop over the test data.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
for i in range(num_test):
dists[i,:] = np.sqrt(np.sum((X[i,:] - self.X_train) ** 2, 1))
return dists
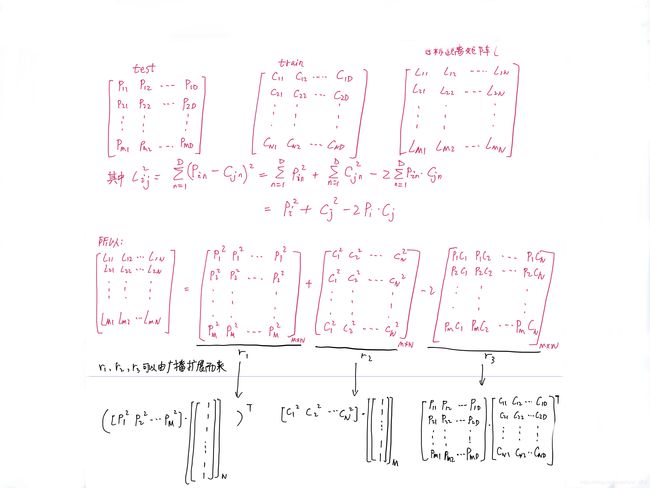
不用循环还一下想不到,其实要计算L2 distance,都是基于一个公式,只不过现在是矩阵而已。辅助理解1,辅助理解2,根据代码里面的提示,感觉辅助理解2里面更符合题目的意思:
再不理解可以看下面这张图:
def compute_distances_no_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using no explicit loops.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
r1=(np.sum(np.square(X), axis=1)*(np.ones((num_train, 1)))).T
r2=np.sum(np.square(self.X_train), axis=1)*(np.ones((num_test, 1)))
r3=-2*np.dot(X, self.X_train.T)
dists = np.sqrt(r1+r2+r3)
return dists
在预测函数里面主要用到了np.argsort函数和max函数的key:
def predict_labels(self, dists, k=1):
"""
Given a matrix of distances between test points and training points,
predict a label for each test point.
Inputs:
- dists: A numpy array of shape (num_test, num_train) where dists[i, j]
gives the distance betwen the ith test point and the jth training point.
Returns:
- y: A numpy array of shape (num_test,) containing predicted labels for the
test data, where y[i] is the predicted label for the test point X[i].
"""
num_test = dists.shape[0]
y_pred = np.zeros(num_test)
for i in range(num_test):
# A list of length k storing the labels of the k nearest neighbors to
# the ith test point.
closest_y = []
#########################################################################
# TODO: #
# Use the distance matrix to find the k nearest neighbors of the ith #
# testing point, and use self.y_train to find the labels of these #
# neighbors. Store these labels in closest_y. #
# Hint: Look up the function numpy.argsort. #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
idx = np.argsort(dists[i,:])[0:k]
closest_y = list(self.y_train[idx])
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
#########################################################################
# TODO: #
# Now that you have found the labels of the k nearest neighbors, you #
# need to find the most common label in the list closest_y of labels. #
# Store this label in y_pred[i]. Break ties by choosing the smaller #
# label. #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
y_pred[i] = max(closest_y, key=closest_y.count)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return y_pred
这是交叉验证的代码,是我第一次写的(那时还不会用一些函数),写的比较ugly,但还能运行,就先放上吧:
import copy
num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]
X_train_folds = []
y_train_folds = []
################################################################################
# TODO: #
# Split up the training data into folds. After splitting, X_train_folds and #
# y_train_folds should each be lists of length num_folds, where #
# y_train_folds[i] is the label vector for the points in X_train_folds[i]. #
# Hint: Look up the numpy array_split function. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
print(X_train.shape)
print(y_train.shape)
X_train_folds = np.array_split(X_train, num_folds, axis = 0)
y_train_folds = np.array_split(y_train, num_folds, axis = 0)
print(len(X_train_folds))
print(len(y_train_folds))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# A dictionary holding the accuracies for different values of k that we find
# when running cross-validation. After running cross-validation,
# k_to_accuracies[k] should be a list of length num_folds giving the different
# accuracy values that we found when using that value of k.
k_to_accuracies = {}
################################################################################
# TODO: #
# Perform k-fold cross validation to find the best value of k. For each #
# possible value of k, run the k-nearest-neighbor algorithm num_folds times, #
# where in each case you use all but one of the folds as training data and the #
# last fold as a validation set. Store the accuracies for all fold and all #
# values of k in the k_to_accuracies dictionary. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
for kk in k_choices:
# 现在X_train_folds,y_train_folds都是列表
accuracy = []
for fold in range(num_folds):
X_temp = copy.deepcopy(X_train_folds)
y_temp = copy.deepcopy(y_train_folds)
X_val = X_temp.pop(fold)
X_tra = np.concatenate(X_temp)
y_val = y_temp.pop(fold)
y_tra = np.concatenate(y_temp)
classifier.train(X_tra, y_tra)
y_val_pred = classifier.predict(X_val,k=kk,num_loops=0)
num_correct = np.sum(y_val_pred == y_val)
accuracy.append(float(num_correct) / X_val.shape[0])
k_to_accuracies[kk] = accuracy
print(k_to_accuracies)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# Print out the computed accuracies
for k in sorted(k_to_accuracies):
for accuracy in k_to_accuracies[k]:
print('k = %d, accuracy = %f' % (k, accuracy))
结果
这是我的交叉验证结果图,超参数k=10结果最好(肉眼估计的),其他结果可直接去看knn.ipynb
最后说一点:我个人认为,做这个cs231n的作业时,有时会遇到自己知识储备中非常陌生的,之前可能一次都没看过学过的知识点,这个时候是可以看一下别人的代码,回过头再有自己的思考,但必须是在自己很努力思考后还没有任何头绪的时候,否则会影响自己的成就感~~
链接
后面的作业博文请见:
- 后一篇的博文:SVM/Softmax classifier