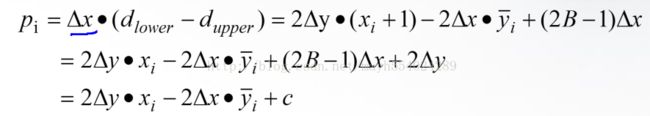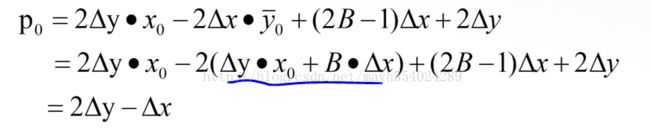bresenham直线，画圆算法（附OpenGL代码）

Bresenham算法画直线：          

  我们在电脑上看到的图像时由一个个像素点拼接而成，当你放大图像就可以观察到这点。以下是一条直线：

 

它是由这些像素点一个一个拼接而成，那么问题来了，怎样选取这些点，使我们看到的更像是一条直线呢？

我们的主要思路就是，谁靠近直线我们就选谁，近水楼台先得月。如下图，因为,所以我们选择直线下面的黄点作为画直线的点。

依照这个原则，直到终点。这样一条线就出来了。所以我们得比较这两个值的大小。我们只考虑0-45度的情况：

 

 

假设直线为 

这里的，而用计算机计算除法是比较耗时的，我们需要改进公式，使其运行更快。这里我们在这个等式前乘以,这样也不会改变等式符号，而我们最终的目的是判断正负，所以是对结果是无影响的。得到如下公式。

其中：

 

此时

对于pi还可以化简，就是将y= mx+b代入

化简得

如果你认为这里就足够简洁了，那么接下来还有更好的。

对pi的迭代：它的好处就是减少计算吧（个人认为，如有高见可探讨），只要判断前一个点的p的值得正负，就可推出下一个点的坐标。然后对进行赋值，再进行下一轮判断以此循环。

 

 bresenham算法画圆：

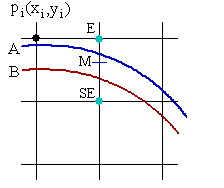
对于画圆算法，主要思路就是取可选点之间的中点，如下图的M：

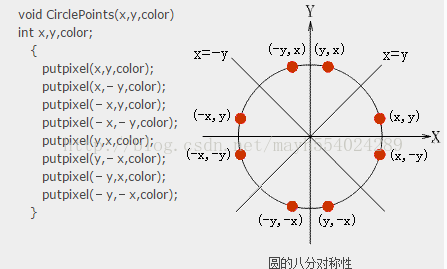
然后判断这个点是在圆内还是在圆外，据此判断所选取的点是E还是SE。然后通过迭代画出1/8个圆，根据八分法，就可以画出整个圆了。

类似直线，推导出的结果就是:

if(di<0) then

           

else

         

迭代至完成1/8圆。

八分法画圆：

       

关于推导，类似于直线，我觉得这两篇有关圆的算法推导写的很详细了，我就不再累赘。

参考文档: 

八分法画圆：http://blog.sina.com.cn/s/blog_9e9ce35f0101b9pd.html 

正负法画圆：http://blog.csdn.net/lwl_ls/article/details/2098659 

完整代码：

#include
#include
#include
using namespace std;

GLfloat pointsize = 1.0f;

void drawOneLine(GLint x, GLint y, GLint x1, GLint y1){
	GLint a = x;
	GLfloat m = (y1 - y)*1.0 / (x1 - x);       //斜率
	GLfloat b = y - m*x;                      
	GLfloat thethay = m*a + b - y;             //thetha y
	GLfloat d0 = 2 * thethay - 1;              //初始化d0
	glPointSize(pointsize);
	GLint cx = x, cy = y;
	glVertex2i(x, y);                         //画第一个点
	while (a <= x1){
		a++;
		thethay = m*a + b - cy;                //更新thetha y
		if (d0 <= 0){                          //更新d0
			d0 += 2 * thethay;
			cy = cy;
		}
		else{
			d0 += 2 * thethay - 2;
			cy = cy + 1;
		}
		glVertex2i(a, cy);
	}

}
void drawbresenhamcycle( GLint R){    //默认原点是0,0 bresenham算法画圆
	GLint a = 0;
	GLint y =(int)(R*1.0/(sqrt(2)));
	GLfloat d0 = 1.25 - R;
	GLfloat d;
	glPointSize(pointsize);
	GLint cx = 0, cy = R;
	glVertex2i(0, 0);
	while (a <= y){
		glVertex2i(a, cy);         //八分画圆
		glVertex2i(-a, -cy);
		glVertex2i(-a, cy);
		glVertex2i(a, -cy);
		glVertex2i(cy, -a);
		glVertex2i(-cy, -a);
		glVertex2i(-cy, a);
		glVertex2i(cy, a);

		a++;
		if (d0 <= 0){
			d0 = d0 + 2 * a + 3;
			cy = cy;
		}
		else{
			d0 = d0 + 2 * (a-cy) +5;
			cy = cy - 1;
		}
	}


}
void drawsigncycle(GLint R){         //正负法画圆
	GLint re = 0;
	GLint x = 0;
	GLint y = R;
	
	glVertex2i(0, 0);
	while (x < (int)(R*1.0 / sqrt(2))){

		glVertex2i(x, y);
		glVertex2i(-x, -y);
		glVertex2i(-x, y);
		glVertex2i(x, -y);
		glVertex2i(y, -x);
		glVertex2i(-y, -x);
		glVertex2i(-y, x);
		glVertex2i(y, x);
		if (re <= 0){
			re = re + 2 * x + 1;
			x = x + 1;
		}
		else{
			re = re - 2 * y + 1;
			y = y - 1;
		}
	}


}

void display(void){          //设置园的半径
	glClear(GL_COLOR_BUFFER_BIT);
	glColor3f(0.0, 1.0f, 0.0f);
	glBegin(GL_POINTS);

	drawOneLine(2, 2, 100, 200);
	drawbresenhamcycle(400);
	drawsigncycle(200);

	glEnd();
	glFlush();
}
int main(int argc, char** argv){
	glutInit(&argc, argv);
	glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
	glutInitWindowPosition(100, 100);
	glutInitWindowSize(800, 800);
	glutCreateWindow("test");
	glClearColor(0.0, 0.0, 0.0, 0.0);
	glMatrixMode(GL_PROJECTION);
	glLoadIdentity();
	gluOrtho2D(-500.0, 800.0,-500.0, 800.0);
	glutDisplayFunc(display);
	glutMainLoop();
	return 0;
}