吴恩达机器学习ex5：正则化线性回归和方差与偏差

1、正则化线性回归
1.1、数据集的可视化
训练数据集：X表示水位变化的历史记录，y表示流出大坝的水量；
交叉验证数据集：Xval，yval；
测试数据集：Xtest，ytest；

其中，训练数据集12组，交叉验证数据集21组，测试数据集21组。

1.2、正则化线性回归损失函数

不对theta0进行惩罚，lambda为正则化参数。
补充函数linearRegCostFunction：

J = (X*theta-y)'*(X*theta-y)/(2*m)+...
    (theta'*theta-theta(1)*theta(1))*lambda/(2*m);

计算得到：

J =

  303.9932

1.3、正则化线性回归梯度
梯度计算公式为：

补充函数linearRegCostFunction：

grad = (X*theta-y)'*X(:,2)/m+lambda*theta/m;
grad(1) = (X*theta-y)'*X(:,1)/m;

计算得到：

grad =

  -15.3030
  598.2507

1.4、训练神经网络
使用函数fmincg对神经网络进行训练，得到的theta为

theta =

   13.0879
    0.3678

作出其拟合函数 y = theta0 + theta1*x:

2、偏差与方差
偏差与方差的权衡是机器学习中的一个重要内容。高偏差的模型结构偏简单趋近于欠拟合，而高方差的模型模型复杂趋近于过拟合。
2.1、学习曲线
学习曲线对于调试学习算法是非常有效的，其横坐标为训练样本的数量，纵坐标为误差（训练误差和交叉验证误差）。
其中训练误差计算公式为：

交叉验证误差计算公式与此类似。
将函数learningCurve补充完整：

for i=1:1:m
    [theta] = trainLinearReg(X(1:i,:), y(1:i,:), lambda);
    error_train(i,1) = linearRegCostFunction(X(1:i,:),y(1:i,:),theta,0);
    error_val(i,1) = linearRegCostFunction(Xval,yval,theta,0);
end

运行程序得到：

# Training Examples	Train Error	Cross Validation Error
  	1		0.000000	205.121096
  	2		0.000000	110.300366
  	3		3.286595	45.010231
  	4		2.842678	48.368911
  	5		13.154049	35.865165
  	6		19.443963	33.829962
  	7		20.098522	31.970986
  	8		18.172859	30.862446
  	9		22.609405	31.135998
  	10		23.261462	28.936207
  	11		24.317250	29.551432
  	12		22.373906	29.433818

观察得知，随着训练样本的增加，训练误差和交叉验证样本误差都很高，这反映出是一个高偏差的问题，即选用的线性回归模型过于简单，不能很好的拟合数据集，为欠拟合状态，因此需要改用复杂的回归函数。
3、多项式回归
假设本次选用的复杂模型为：

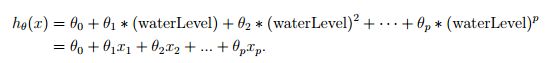
3.1、学习多项式回归
选取多项式次数为8，即p=8。
首先补充完整polyFeatures函数，该函数的目的是将一维X，扩大为p维X。

for i = 1:p
        X_poly(:,i) = X.^i;
end

p = 8;

% Map X onto Polynomial Features and Normalize
X_poly = polyFeatures(X, p);
[X_poly, mu, sigma] = featureNormalize(X_poly);  % Normalize
X_poly = [ones(m, 1), X_poly];                   % Add Ones

% Map X_poly_test and normalize (using mu and sigma)
X_poly_test = polyFeatures(Xtest, p);
X_poly_test = bsxfun(@minus, X_poly_test, mu);
X_poly_test = bsxfun(@rdivide, X_poly_test, sigma);
X_poly_test = [ones(size(X_poly_test, 1), 1), X_poly_test];         % Add Ones

% Map X_poly_val and normalize (using mu and sigma)
X_poly_val = polyFeatures(Xval, p);
X_poly_val = bsxfun(@minus, X_poly_val, mu);
X_poly_val = bsxfun(@rdivide, X_poly_val, sigma);
X_poly_val = [ones(size(X_poly_val, 1), 1), X_poly_val];           % Add Ones

对于该段代码解释如下：
X_poly = polyFeatures(X, p)是将特征参数扩大为多项式特征参数；
[X_poly, mu, sigma] = featureNormalize(X_poly)返回归一化后特征参数集，其中返回值mu为每个特征参数的均值（期望），返回值sigma为每个特征参数的标准差，其归一化方法为X-mu/sigma；
X_poly = [ones(m, 1), X_poly]增加第一列为1；

同理，对于X_poly_test特征参数：
X_poly_test = polyFeatures(Xtest, p)将特征参数矩阵扩大为p阶多项式特征参数；
X_poly_test = bsxfun(@minus, X_poly_test, mu)使用X_poly_test-mu按列进行处理；
X_poly_test = bsxfun(@rdivide, X_poly_test, sigma)使用X_poly_test/sigma按列进行处理，综合上行代码即为X_poly_test-mu/sigma，为归一化操作；

此处，仍然使用训练集的mu和sigma两个参数对于交叉验证集和测试集进行归一化的原因：此处的归一化后的特征参数集是为训练theta值准备的，而theta值只能从训练集中训练获得，若交叉验证集和测试集独立对自身进行归一化，此处将失去其验证集和测试集的功能定位，所以所有的参数均应该从训练集中获得，而交叉验证集和测试集仅为验证使用。

归一化后获取到的三个数据集为：



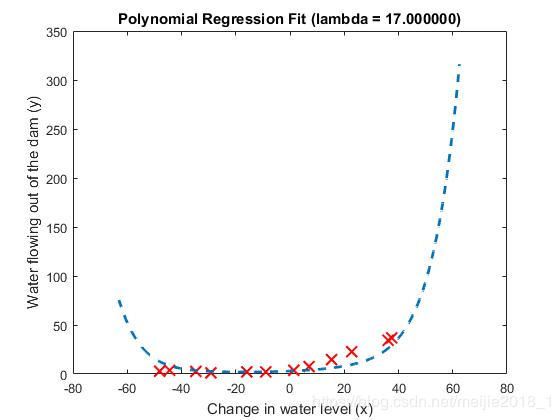
当lambda=0，绘制出拟合曲线有：

训练误差和交叉验证误差的关系：

可以看到交叉验证误差比训练误差高很多，并且越来越高，因此为高方差状态，过拟合，需要进行正则化。
3.3、正则化参数lambda的选择
补充完整validationCurve函数

function [lambda_vec, error_train, error_val] = ...
    validationCurve(X, y, Xval, yval)

% Selected values of lambda (you should not change this)
lambda_vec = [0 0.001 0.003 0.01 0.03 0.1 0.3 1 3 10 15 20 25]';

% You need to return these variables correctly.
error_train = zeros(length(lambda_vec), 1);
error_val = zeros(length(lambda_vec), 1);

for i = 1:length(lambda_vec)
    lambda = lambda_vec(i);
    [theta] = trainLinearReg(X, y, lambda);
    error_train(i,1) = linearRegCostFunction(X,y,theta,0);
    error_val(i,1) = linearRegCostFunction(Xval,yval,theta,0);
end
end

运行程序有：

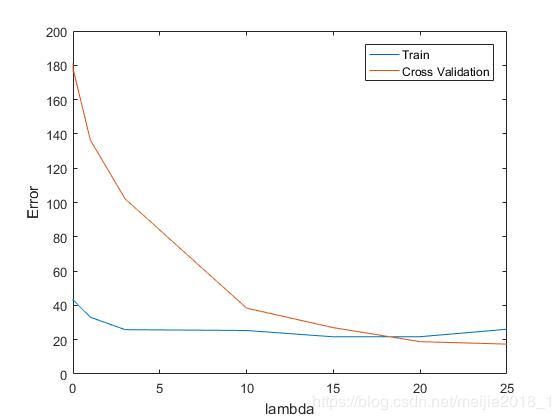
可知当正则化参数lambda=17左右时效果最佳。
返回3.1，设置lambda=17，绘制拟合曲线、训练误差和交叉验证误差有：