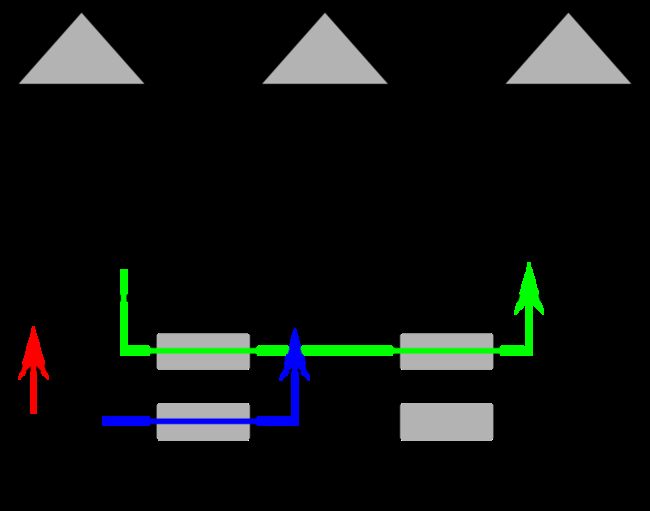
1020A - New Building for SIS
A. New Building for SIS
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output
You are looking at the floor plan of the Summer Informatics School's new building. You were tasked with SIS logistics, so you really care about travel time between different locations: it is important to know how long it would take to get from the lecture room to the canteen, or from the gym to the server room.
The building consists of n towers, h floors each, where the towers are labeled from 1 to n, the floors are labeled from 1 to h. There is a passage between any two adjacent towers (two towers i and i + 1 for all i: 1 ≤ i ≤ n - 1) on every floor x, where a ≤ x ≤ b. It takes exactly one minute to walk between any two adjacent floors of a tower, as well as between any two adjacent towers, provided that there is a passage on that floor. It is not permitted to leave the building.
The picture illustrates the first example.
You have given k pairs of locations (ta, fa), (tb, fb): floor fa of tower ta and floor fb of tower tb. For each pair you need to determine the minimum walking time between these locations.
Input
The first line of the input contains following integers:
- n: the number of towers in the building (1 ≤ n ≤ 108),
- h: the number of floors in each tower (1 ≤ h ≤ 108),
- a and b: the lowest and highest floor where it's possible to move between adjacent towers (1 ≤ a ≤ b ≤ h),
- k: total number of queries (1 ≤ k ≤ 104).
Next k lines contain description of the queries. Each description consists of four integers ta, fa, tb, fb (1 ≤ ta, tb ≤ n, 1 ≤ fa, fb ≤ h). This corresponds to a query to find the minimum travel time between fa-th floor of the ta-th tower and fb-th floor of the tb-th tower.
Output
For each query print a single integer: the minimum walking time between the locations in minutes.
Example
input
Copy
3 6 2 3 3 1 2 1 3 1 4 3 4 1 2 2 3
output
Copy
1 4 2
题意:有n栋楼,从一栋楼某个地方,到大另一栋楼的某个地方,每栋楼给了连接楼的天桥,每走一层或者穿个一栋楼花费一分钟,求出起点到大目的点最少花费的时间。
题解:模拟 分三种情况,细分的话就是四种,一是在同一楼移动,只需要算楼层差就行,二是起点和终点都在天桥上,所以要先王下走到达天桥,然后往上走,三是起点终点都天桥下,需要先往上走,到达天桥,穿过天桥,再往下,第四种就是斜走法,左上到右下,或者右下到左上,或者水平通过天桥。直接算坐标差。
c++:
#include
using namespace std;
int main()
{
int n,h,a,b,k,ta,fa,tb,fb,ans;
cin>>n>>h>>a>>b>>k;
while(k--)
{
cin>>ta>>fa>>tb>>fb;
ans=0;
if(ta==tb) ans=abs(fa-fb);
else if(fa>a&&fa>b&&fb>a&&fb>b) ans=abs(ta-tb)+abs(fa-fb)+min(fa-b,fb-b)*2;
else if(fa python:
n,h,a,b,k=map(int,input().split())
for i in range(k):
ans=0
ta,fa,tb,fb=map(int,input().split())
ans+=abs(ta-tb)+abs(fa-fb)
if ta!=tb:
if fa>b and fb>b:ans+=min(fa-b,fb-b)*2
if fa