Python实现FIR带通滤波器

1、FIR算法实现

$y(0)={\sum }_0^{N}h(i)x(i)$

class filter:
    def __init__(self,order,h):
        self.order=order
        self.h=h
        self.output=[]
    def FIR_Filter(self,vi):
        for i in range(len(vi)):
            sum=0
            if i < self.order:
                for j in range(i):
                    sum=sum + self.h[j]*vi[i-j]
            else:      
                for j in range(self.order):
                    sum=sum + self.h[j]*vi[i-j]
                
            self.output.append(sum)   
        return self.output
        
       

2、利用fdatool生成带通滤波参数

Weight=[ -0.001509991125, 0.001329824561, 0.005089743994,0.0004591136531,-0.003339873627,
   0.002003055066, -0.01155735459, -0.02634175681,  0.01259854902,    0.036990989,
   0.001854708185,  0.03572623804,  0.06532743573,  -0.1264344603,  -0.2432653308,
    0.07677905262,   0.3491531909,  0.07677905262,  -0.2432653308,  -0.1264344603,
    0.06532743573,  0.03572623804, 0.001854708185,    0.036990989,  0.01259854902,
   -0.02634175681, -0.01155735459, 0.002003055066,-0.003339873627,0.0004591136531,
   0.005089743994, 0.001329824561]

2.1 生成数据源

x=np.linspace(0,1,1200)
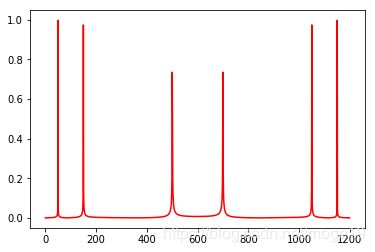
#设置需要采样的信号，频率分量有50，150和500
y=np.sin(2*np.pi*50*x) + np.sin(2*np.pi*150*x)+np.sin(2*np.pi*500*x)

利用FIR滤波：

FIR_filter=filter(32,Weight)
output = FIR_filter.FIR_Filter(y)

利用FFT分析比较：

分析源信号:

yy=fft(y)                     #快速傅里叶变换
yf=abs(fft(y))                # 取模
yf1=abs(fft(y))/((len(x)/2))           #归一化处理
yf2 = yf1[range(int(len(x)/2))]  #由于对称性，只取一半区间
plt.figure(1)
plt.plot(xf,yf1,'r') #显示原始信号的FFT模值

分析FIR滤波后的数据：

yy_1=fft(output)                     #快速傅里叶变换
yf_1=abs(fft(output))                # 取模
yf1_1=abs(fft(output))/((len(x)/2))           #归一化处理
yf2_1 = yf1_1[range(int(len(x)/2))]  #由于对称性，只取一半区间
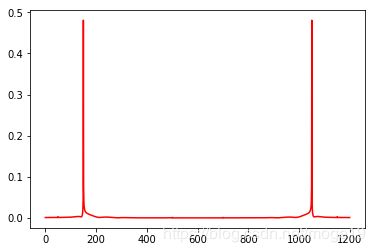
plt.plot(xf,yf1_1,'r') #显示原始信号的FFT模值

滤波后的信号与原数据比较：
参考源码：

Weight=[ -0.001509991125, 0.001329824561, 0.005089743994,0.0004591136531,-0.003339873627,
   0.002003055066, -0.01155735459, -0.02634175681,  0.01259854902,    0.036990989,
   0.001854708185,  0.03572623804,  0.06532743573,  -0.1264344603,  -0.2432653308,
    0.07677905262,   0.3491531909,  0.07677905262,  -0.2432653308,  -0.1264344603,
    0.06532743573,  0.03572623804, 0.001854708185,    0.036990989,  0.01259854902,
   -0.02634175681, -0.01155735459, 0.002003055066,-0.003339873627,0.0004591136531,
   0.005089743994, 0.001329824561]
class filter:
    def __init__(self,order,h):
        self.order=order
        self.h=h
        self.output=[]
    def FIR_Filter(self,vi):
        for i in range(len(vi)):
            sum=0
            if i < self.order:
                for j in range(i):
                    sum=sum + self.h[j]*vi[i-j]
            else:      
                for j in range(self.order):
                    sum=sum + self.h[j]*vi[i-j]
                
            self.output.append(sum)   
        return self.output
        

#采样点选择1400个，因为设置的信号频率分量最高为600Hz，根据采样定理知采样频率要大于信号频率2倍，所以这里设置采样频率为1400Hz（即一秒内有1400个采样点）
x=np.linspace(0,1,1200)
#设置需要采样的信号，频率分量有180，390和600
y=np.sin(2*np.pi*50*x) + np.sin(2*np.pi*150*x)+np.sin(2*np.pi*500*x)
yc=np.sin(2*np.pi*150*x)
yy=fft(y)                     #快速傅里叶变换
yf=abs(fft(y))                # 取模
yf1=abs(fft(y))/((len(x)/2))           #归一化处理
yf2 = yf1[range(int(len(x)/2))]  #由于对称性，只取一半区间
plt.figure(1)
plt.plot(xf,yf1,'r') #显示原始信号的FFT模值

#混合波的FFT（双边频率范围）
xf = np.arange(len(y))        # 频率
FIR_filter=filter(32,Weight)
output = FIR_filter.FIR_Filter(y)

yy_1=fft(output)                     #快速傅里叶变换
yf_1=abs(fft(output))                # 取模
yf1_1=abs(fft(output))/((len(x)/2))           #归一化处理
yf2_1 = yf1_1[range(int(len(x)/2))]  #由于对称性，只取一半区间

plt.figure(2)
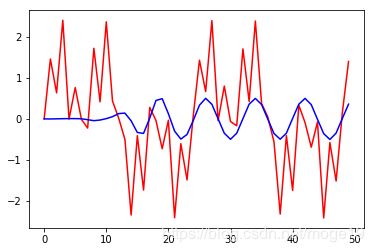
plt.plot(y[0:50],'r') #显示原始信号的FFT模值
plt.plot(output[0:50],'b') #显示原始信号的FFT模值
#plt.plot(yc[0:50],'y') #显示原始信号的FFT模值
plt.figure(3)
#plt.plot(xf,yf1,'b') #显示原始信号的FFT模值
plt.plot(xf,yf1_1,'r') #显示原始信号的FFT模值