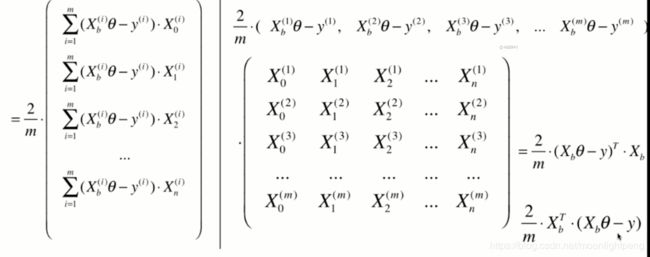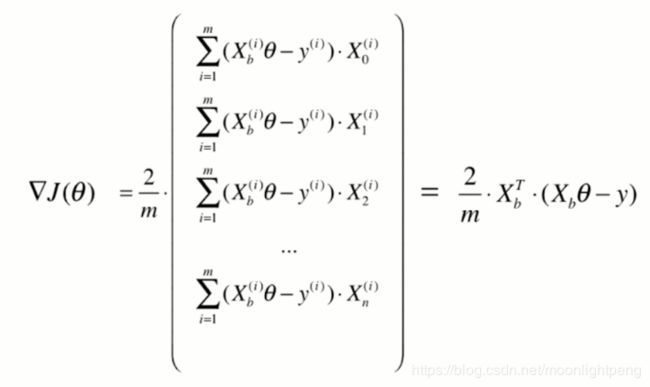第六章 线性回归 学习笔记中

 

目录

6.4在线性回归模型中使用梯度下降法04-Implement-Gradient-Descent-in-Linear-Regression

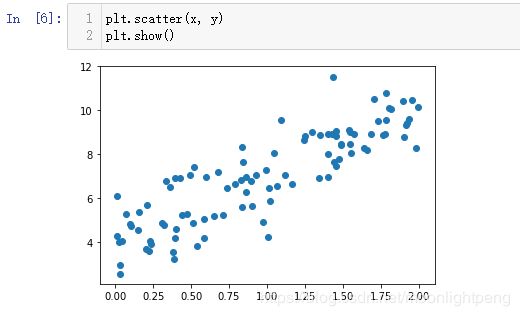
使用梯度下降法训练

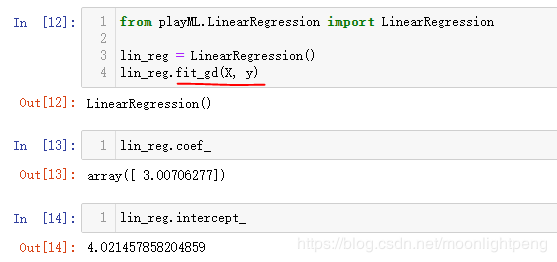
封装我们的线性回归算法

LinearRegression.py

6-5 梯度下降的向量化和数据标准化

梯度下降法的向量化

使用梯度下降法

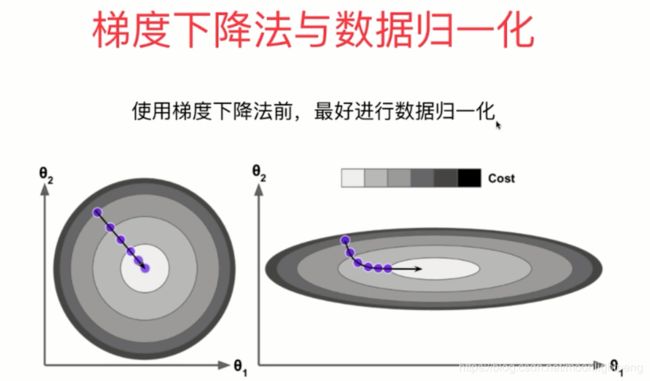
使用梯度下降法前进行数据归一化

梯度下降法的优势

6-6 随机梯度下降法

随机梯度下降法

---

 

在线性回归模型中使用梯度下降法04-Implement-Gradient-Descent-in-Linear-Regression

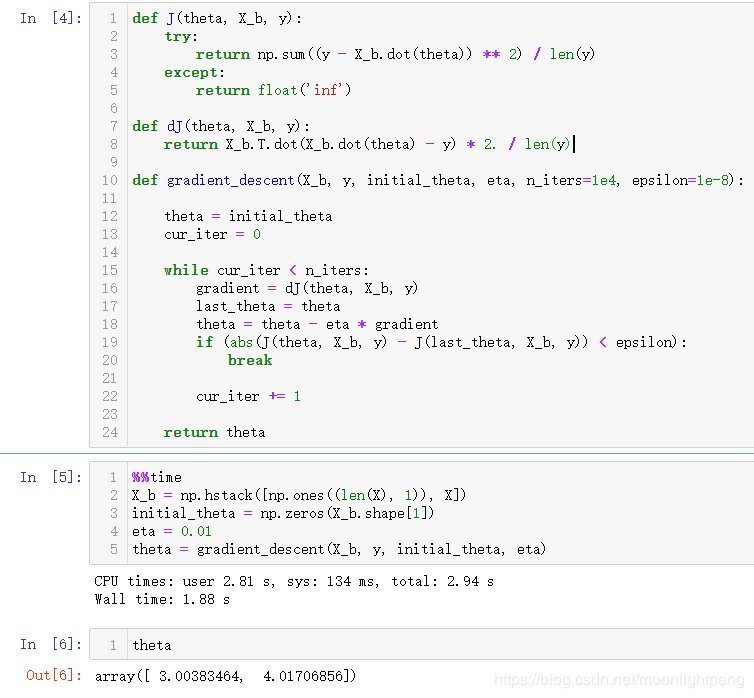
使用梯度下降法训练

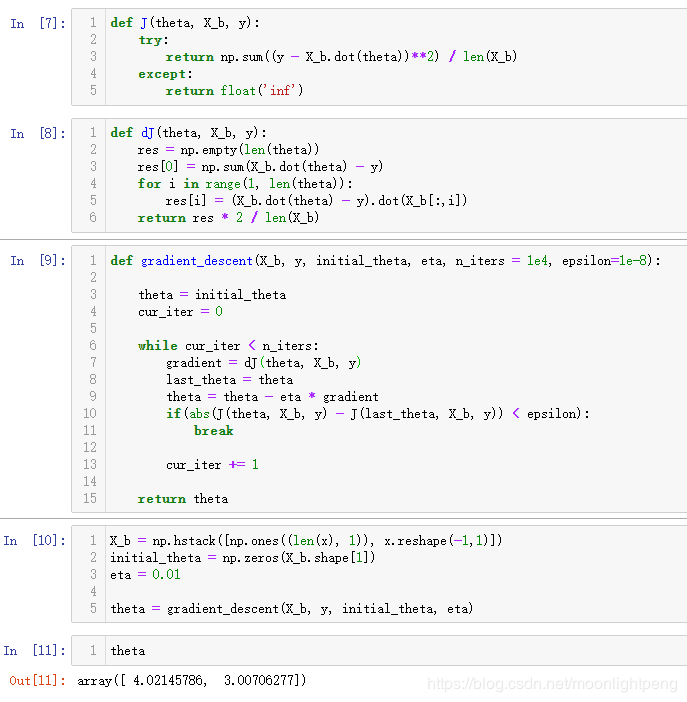
def J(theta, X_b, y):
    try:
        return np.sum((y - X_b.dot(theta))**2) / len(X_b)
    except:
        return float('inf')

def dJ(theta, X_b, y):
    res = np.empty(len(theta))
    res[0] = np.sum(X_b.dot(theta) - y)
    for i in range(1, len(theta)):
        res[i] = (X_b.dot(theta) - y).dot(X_b[:,i])
    return res * 2 / len(X_b)

res[0]的计算公式不懂，y,X_b都是矩阵呀？？？？？？？？

def gradient_descent(X_b, y, initial_theta, eta, n_iters = 1e4, epsilon=1e-8):
    
    theta = initial_theta
    cur_iter = 0

    while cur_iter < n_iters:
        gradient = dJ(theta, X_b, y)
        last_theta = theta
        theta = theta - eta * gradient
        if(abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
            break
            
        cur_iter += 1

    return theta

X_b = np.hstack([np.ones((len(x), 1)), x.reshape(-1,1)])
initial_theta = np.zeros(X_b.shape[1])
eta = 0.01

theta = gradient_descent(X_b, y, initial_theta, eta)

封装我们的线性回归算法

LinearRegression.py

import numpy as np
from .metrics import r2_score

class LinearRegression:

    def __init__(self):
        """初始化Linear Regression模型"""
        self.coef_ = None
        self.intercept_ = None
        self._theta = None

    def fit_normal(self, X_train, y_train):
        """根据训练数据集X_train, y_train训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"

        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)

        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
        """根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"

        def J(theta, X_b, y):
            try:
                return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
            except:
                return float('inf')

        def dJ(theta, X_b, y):
            res = np.empty(len(theta))
            res[0] = np.sum(X_b.dot(theta) - y)
            for i in range(1, len(theta)):
                res[i] = (X_b.dot(theta) - y).dot(X_b[:, i])
            return res * 2 / len(X_b)

        def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):

            theta = initial_theta
            cur_iter = 0

            while cur_iter < n_iters:
                gradient = dJ(theta, X_b, y)
                last_theta = theta
                theta = theta - eta * gradient
                if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
                    break

                cur_iter += 1

            return theta

        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        initial_theta = np.zeros(X_b.shape[1])
        self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)

        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def predict(self, X_predict):
        """给定待预测数据集X_predict，返回表示X_predict的结果向量"""
        assert self.intercept_ is not None and self.coef_ is not None, \
            "must fit before predict!"
        assert X_predict.shape[1] == len(self.coef_), \
            "the feature number of X_predict must be equal to X_train"

        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
        return X_b.dot(self._theta)

    def score(self, X_test, y_test):
        """根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""

        y_predict = self.predict(X_test)
        return r2_score(y_test, y_predict)

    def __repr__(self):
        return "LinearRegression()"

6-5 梯度下降的向量化和数据标准化

 

numpy中表示不分行和列向量，但上面是1*（n+1）的行向量

但计算时要区分,梯度是列向量，要转置 

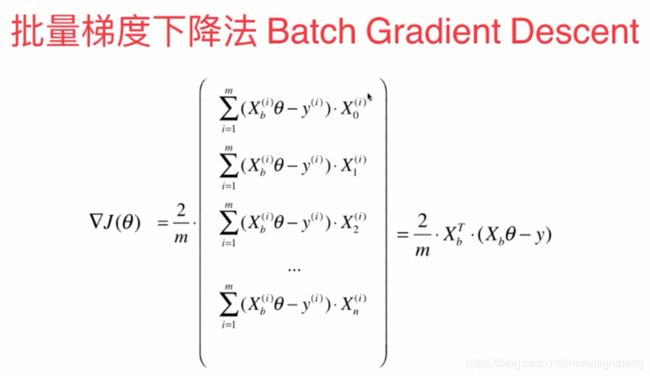
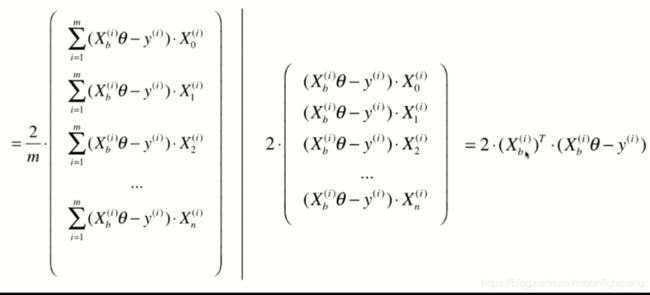
将求梯度的过程进行了向量化

梯度下降法的向量化

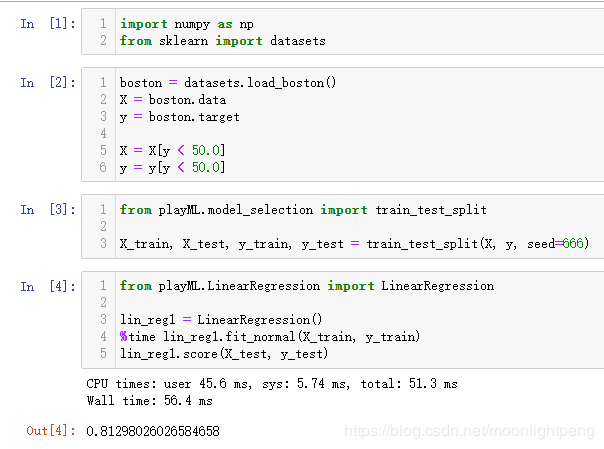
通过正规方程求解

model_selection.py

import numpy as np


def train_test_split(X, y, test_ratio=0.2, seed=None):
    """将数据 X 和 y 按照test_ratio分割成X_train, X_test, y_train, y_test"""
    assert X.shape[0] == y.shape[0], \
        "the size of X must be equal to the size of y"
    assert 0.0 <= test_ratio <= 1.0, \
        "test_ration must be valid"

    if seed:
        np.random.seed(seed)

    shuffled_indexes = np.random.permutation(len(X))

    test_size = int(len(X) * test_ratio)
    test_indexes = shuffled_indexes[:test_size]
    train_indexes = shuffled_indexes[test_size:]

    X_train = X[train_indexes]
    y_train = y[train_indexes]

    X_test = X[test_indexes]
    y_test = y[test_indexes]

    return X_train, X_test, y_train, y_test

 

LinearRegression.py

import numpy as np
from .metrics import r2_score

class LinearRegression:

    def __init__(self):
        """初始化Linear Regression模型"""
        self.coef_ = None
        self.intercept_ = None
        self._theta = None

    def fit_normal(self, X_train, y_train):
        """根据训练数据集X_train, y_train训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"

        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)

        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
        """根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"

        def J(theta, X_b, y):
            try:
                return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
            except:
                return float('inf')
            
        def dJ(theta, X_b, y):
            return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y)

        def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):

            theta = initial_theta
            cur_iter = 0

            while cur_iter < n_iters:
                gradient = dJ(theta, X_b, y)
                last_theta = theta
                theta = theta - eta * gradient
                if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
                    break

                cur_iter += 1

            return theta

        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        initial_theta = np.zeros(X_b.shape[1])
        self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)

        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def predict(self, X_predict):
        """给定待预测数据集X_predict，返回表示X_predict的结果向量"""
        assert self.intercept_ is not None and self.coef_ is not None, \
            "must fit before predict!"
        assert X_predict.shape[1] == len(self.coef_), \
            "the feature number of X_predict must be equal to X_train"

        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
        return X_b.dot(self._theta)

    def score(self, X_test, y_test):
        """根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""

        y_predict = self.predict(X_test)
        return r2_score(y_test, y_predict)

    def __repr__(self):
        return "LinearRegression()"

使用梯度下降法

报错了，有警告， overflow

coef是NAN是无穷大

之前的没有除m会出现这样的情况

这个真实的数据集，每一个特征的其规模不同有的0.1, 有的大于100

手动的给一个eta很小的值

现在没有错，但其结果不好，不是最小值，下降的很慢，也许需要更多的迭代次数才能有好的结果，n_iters = 1e6，这么多可能比较耗时，记时一下

0.754,可以需要更多的循环次数，但太耗时，所以其问题是其特征不在一个规模上，需要数据规一化处理

不在一个维度上其步长或者太大，或者太小

 

使用梯度下降法前进行数据归一化

梯度下降法的优势

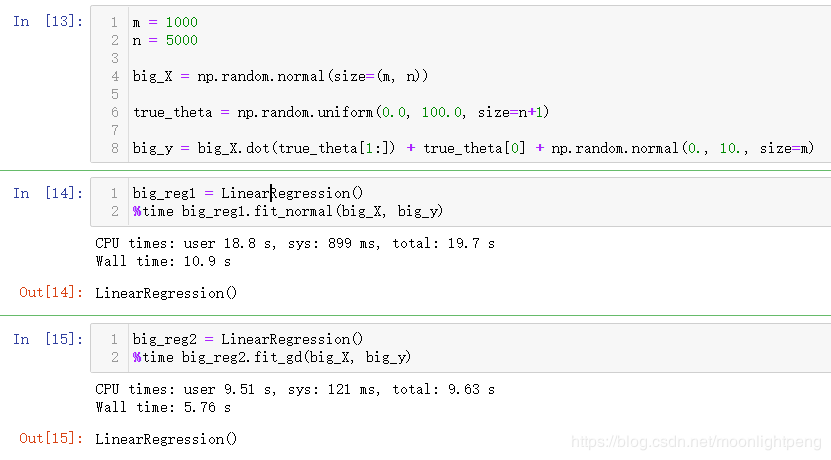
维数增大时，正规方程处理的矩阵耗时多，

样本数小于特征数，要让每一个样本都参与计算，这使得计算比较慢，有一个改进的方案即随机梯度下降法

6-6 随机梯度下降法

 

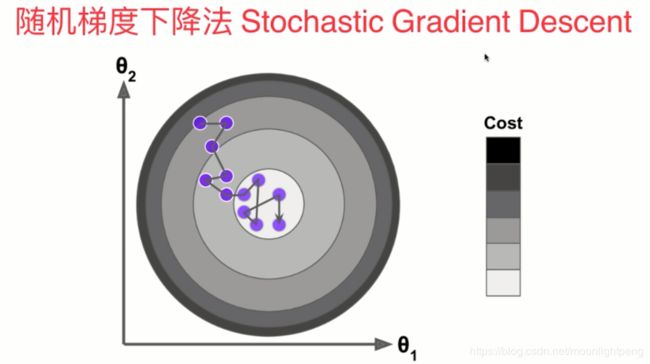
上面的所有样本都计算，所以称批量的，但样本太大时太耗时

随机一个，指搜索的方向，xb是一行，任意的取一个i值

批量的方向固定，一直向前

随机不能保证下降最快或在下降的方向，有一定的不可欲知性，但实验证明

如果样本太大时愿意用精度换时间

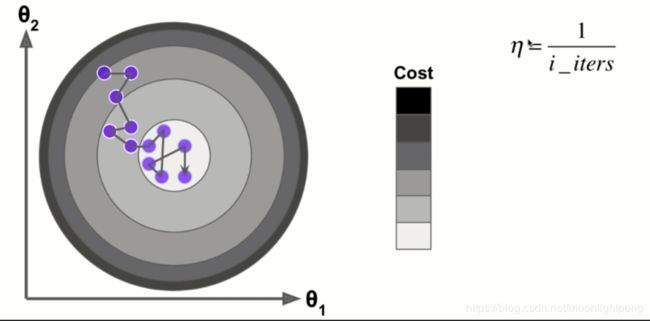
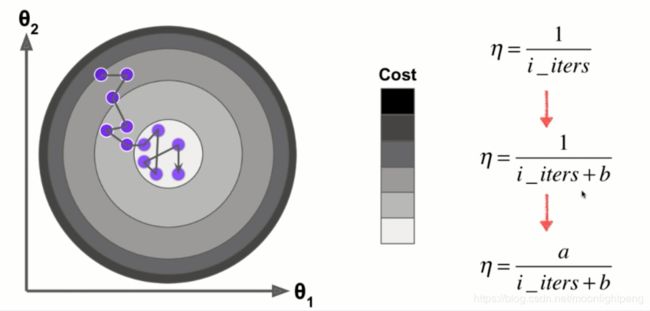
随机时其学习率的选择就非常重要，学习率前面大后面小，最简单的方法就是循环次数的倒数

其问题是循环次数太小时，其变化会非常快，前后其下降的比率差别太大

可改进为，同时分子为1有时也效果不太好，所以公式优化为

 

其逐渐下降的过程与模拟退火的思想一致

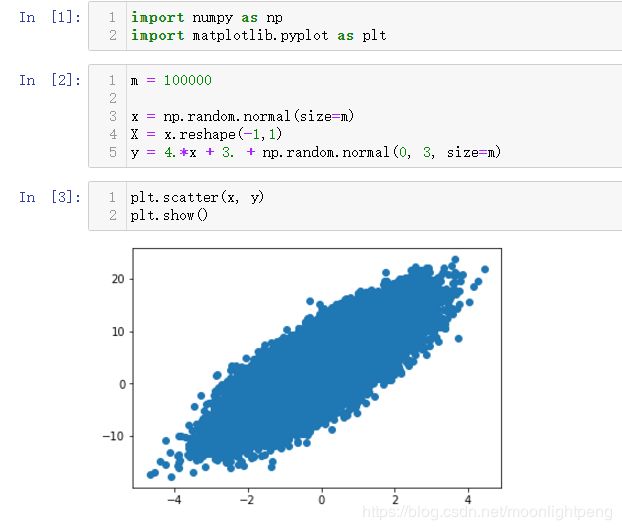
为了体现随机的优势其样本比较大

 

 

先使用正规方程的思路求解

def J(theta, X_b, y):
    try:
        return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
    except:
        return float('inf')
    
def dJ(theta, X_b, y):
    return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y)

def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):

    theta = initial_theta
    cur_iter = 0

    while cur_iter < n_iters:
        gradient = dJ(theta, X_b, y)
        last_theta = theta
        theta = theta - eta * gradient
        if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
            break

        cur_iter += 1

    return theta

 

随机梯度下降法

 

x_b是某一行，y也是一个值

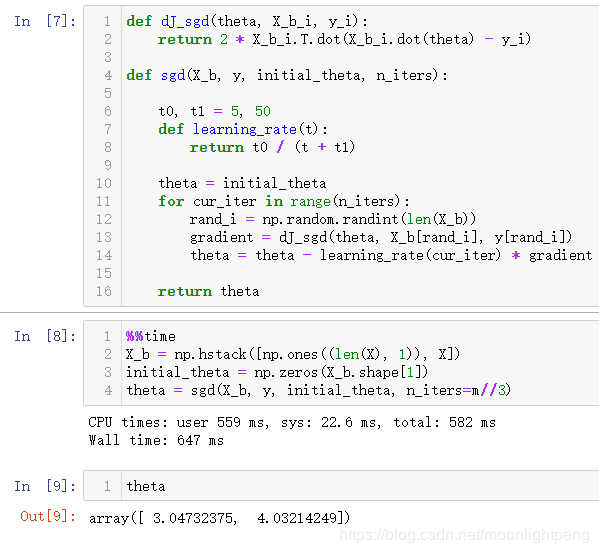
随机用了样本的三分之一，时间肯定要快

def dJ_sgd(theta, X_b_i, y_i):
    return 2 * X_b_i.T.dot(X_b_i.dot(theta) - y_i)

def sgd(X_b, y, initial_theta, n_iters):

    t0, t1 = 5, 50
    def learning_rate(t):
        return t0 / (t + t1)

    theta = initial_theta
    for cur_iter in range(n_iters):
        rand_i = np.random.randint(len(X_b))
        gradient = dJ_sgd(theta, X_b[rand_i], y[rand_i])
        theta = theta - learning_rate(cur_iter) * gradient

    return theta