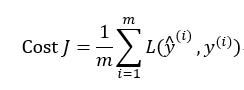B站吴恩达深度学习视频笔记(27)——为什么使用卷积
前言
啊,不得不说吴恩达使用的例子非常难描述。所以我偷懒用Keras做了卷积的小例子。但是这节课要用到之前的例子了,所以我不得不把应该在上节课的例子再补上。哎,该来的还是要来,逃不掉的。
卷积神经网络实例
构建全卷积神经网络的构造模块我们已经掌握得差不多了,下面来看个例子。
假设,有一张大小为32×32×3的输入图片,这是一张RGB模式的图片,你想做手写体数字识别。32×32×3的RGB图片中含有某个数字,比如7,你想识别它是从0-9这10个数字中的哪一个,我们构建一个神经网络来实现这个功能。
我用的这个网络模型和经典网络LeNet-5非常相似,灵感也来源于此。LeNet-5是多年前Yann LeCun创建的,我所采用的模型并不是LeNet-5,但是受它启发,许多参数选择都与LeNet-5相似。输入是32×32×3的矩阵,假设第一层使用过滤器大小为5×5,步幅是1,padding是0,过滤器个数为6,那么输出为28×28×6。将这层标记为CONV1,它用了6个过滤器,增加了偏差,应用了非线性函数,可能是ReLU非线性函数,最后输出CONV1的结果。
然后构建一个池化层,这里我选择用最大池化,参数f=2,s=2,因为padding为0,我就不写出来了。现在开始构建池化层,最大池化使用的过滤器为2×2,步幅为2,表示层的高度和宽度会减少一半。因此,28×28变成了14×14,通道数量保持不变,所以最终输出为14×14×6,将该输出标记为POOL1。
人们发现在卷积神经网络文献中,卷积有两种分类,这与所谓层的划分存在一致性。
一类卷积是一个卷积层和一个池化层一起作为一层,这就是神经网络的Layer1。
另一类卷积是把卷积层作为一层,而池化层单独作为一层。人们在计算神经网络有多少层时,通常只统计具有权重和参数的层。因为池化层没有权重和参数,只有一些超参数。
这里,我们把CONV1和POOL1共同作为一个卷积,并标记为Layer1。虽然你在阅读网络文章或研究报告时,你可能会看到卷积层和池化层各为一层的情况,这只是两种不同的标记术语。一般我在统计网络层数时,只计算具有权重的层,也就是把CONV1和POOL1作为Layer1。这里我们用CONV1和POOL1来标记,两者都是神经网络Layer1的一部分,POOL1也被划分在Layer1中,因为它没有权重,得到的输出是14×14×6。
我们再为它构建一个卷积层,过滤器大小为5×5,步幅为1,这次我们用10个过滤器,最后输出一个10×10×10的矩阵,标记为CONV2。
然后做最大池化,超参数f=2,s=2。你大概可以猜出结果,f=2,s=2,高度和宽度会减半,最后输出为5×5×10,标记为POOL2,这就是神经网络的第二个卷积层,即Layer2。
如果对Layer1应用另一个卷积层,过滤器为5×5,即f=5,步幅是1,padding为0,所以这里省略了,过滤器16个,所以CONV2输出为10×10×16。我们看看CONV2,这是CONV2层。
继续执行做大池化计算,参数f=2,s=2,你能猜到结果么?对10×10×16输入执行最大池化计算,参数f=2,s=2,高度和宽度减半,计算结果猜到了吧。最大池化的参数f=2,s=2,输入的高度和宽度会减半,结果为5×5×16,通道数和之前一样,标记为POOL2。这是一个卷积,即Layer2,因为它只有一个权重集和一个卷积层CONV2。
5×5×16矩阵包含400个元素,现在将POOL2平整化为一个大小为400的一维向量。我们可以把平整化结果想象成这样的一个神经元集合,然后利用这400个单元构建下一层。下一层含有120个单元,这就是我们第一个全连接层,标记为FC3。这400个单元与120个单元紧密相连,这就是全连接层。它很像我们在第一和第二门课中讲过的单神经网络层,这是一个标准的神经网络。它的权重矩阵为W1 ,维度为120×40。这就是所谓的“全连接”,因为这400个单元与这120个单元的每一项连接,还有一个偏差参数。最后输出120个维度,因为有120个输出。
然后我们对这个120个单元再添加一个全连接层,这层更小,假设它含有84个单元,标记为FC4。
最后,用这84个单元填充一个softmax单元。如果我们想通过手写数字识别来识别手写0-9这10个数字,这个softmax就会有10个输出。
此例中的卷积神经网络很典型,看上去它有很多超参数,关于如何选定这些参数,后面我提供更多建议。常规做法是,尽量不要自己设置超参数,而是查看文献中别人采用了哪些超参数,选一个在别人任务中效果很好的架构,那么它也有可能适用于你自己的应用程序,这块下周我会细讲。
现在,我想指出的是,随着神经网络深度的加深,高度n_H和宽度n_W通常都会减少,前面我就提到过,从32×32到28×28,到14×14,到10×10,再到5×5。所以随着层数增加,高度和宽度都会减小,而通道数量会增加,从3到6到16不断增加,然后得到一个全连接层。
在神经网络中,另一种常见模式就是一个或多个卷积后面跟随一个池化层,然后一个或多个卷积层后面再跟一个池化层,然后是几个全连接层,最后是一个softmax。这是神经网络的另一种常见模式。
接下来我们讲讲神经网络的激活值形状,激活值大小和参数数量。输入为32×32×3,这些数做乘法,结果为3072,所以激活值a^([0])有3072维,激活值矩阵为32×32×3,输入层没有参数。计算其他层的时候,试着自己计算出激活值,这些都是网络中不同层的激活值形状和激活值大小。
有几点要注意:
第一,池化层和最大池化层没有参数;
第二卷积层的参数相对较少,前面课上我们提到过,其实许多参数都存在于神经网络的全连接层。
观察可发现,随着神经网络的加深,激活值尺寸会逐渐变小,如果激活值尺寸下降太快,也会影响神经网络性能。示例中,激活值尺寸在第一层为6000,然后减少到1600,慢慢减少到84,最后输出softmax结果。我们发现,许多卷积网络都具有这些属性,模式上也相似。
神经网络的基本构造模块我们已经讲完了,一个卷积神经网络包括卷积层、池化层和全连接层。
许多计算机视觉研究正在探索如何把这些基本模块整合起来,构建高效的神经网络,整合这些基本模块确实需要深入的理解。
根据我的经验,找到整合基本构造模块最好方法就是大量阅读别人的案例。
下周会演示一些整合基本模块,成功构建高效神经网络的具体案例。希望下周的课程可以帮助你找到构建有效神经网络的感觉,或许你也可以将别人开发的框架应用于自己的应用程序,这是下周的内容。下节课,也是本周最后一节课,我想花点时间讨论下,为什么大家愿意使用卷积,使用卷积的好处和优势是什么,以及如何整合多个卷积,如何检验神经网络,如何在训练集上训练神经网络来识别图片或执行其他任务,我们下节笔记继续讲。
为什么使用卷积
我们来分析一下卷积在神经网络中如此受用的原因,然后对如何整合这些卷积,如何通过一个标注过的训练集训练卷积神经网络做个简单概括。和只用全连接层相比,卷积层的两个主要优势在于参数共享和稀疏连接,举例说明一下。
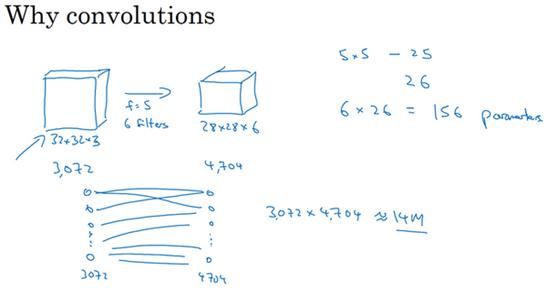
假设有一张32×32×3维度的图片,这是上节课的示例,假设用了6个大小为5×5的过滤器,输出维度为28×28×6。32×32×3=3072,28×28×6=4704。我们构建一个神经网络,其中一层含有3072个单元,下一层含有4074个单元,两层中的每个神经元彼此相连,然后计算权重矩阵,它等于4074×3072≈1400万,所以要训练的参数很多。
虽然以现在的技术,我们可以用1400多万个参数来训练网络,因为这张32×32×3的图片非常小,训练这么多参数没有问题。如果这是一张1000×1000的图片,权重矩阵会变得非常大。我们看看这个卷积层的参数数量,每个过滤器都是5×5,一个过滤器有25个参数,再加上偏差参数,那么每个过滤器就有26个参数,一共有6个过滤器,所以参数共计156个,参数数量还是很少。
卷积网络映射这么少参数有两个原因:
一是参数共享。
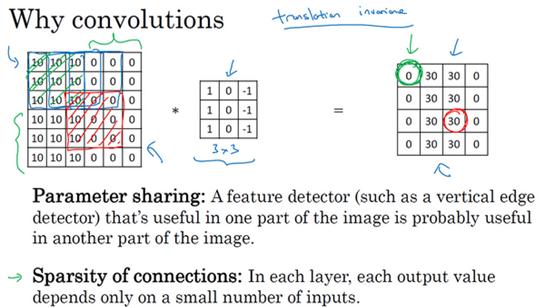
观察发现,特征检测如垂直边缘检测如果适用于图片的某个区域,那么它也可能适用于图片的其他区域。也就是说,如果你用一个3×3的过滤器检测垂直边缘,那么图片的左上角区域,以及旁边的各个区域(左边矩阵中蓝色方框标记的部分)都可以使用这个3×3的过滤器。每个特征检测器以及输出都可以在输入图片的不同区域中使用同样的参数,以便提取垂直边缘或其它特征。
它不仅适用于边缘特征这样的低阶特征,同样适用于高阶特征,例如提取脸上的眼睛,猫或者其他特征对象。即使减少参数个数,这9个参数同样能计算出16个输出。
直观感觉是,一个特征检测器,如垂直边缘检测器用于检测图片左上角区域的特征,这个特征很可能也适用于图片的右下角区域。因此在计算图片左上角和右下角区域时,你不需要添加其它特征检测器。假如有一个这样的数据集,其左上角和右下角可能有不同分布,也有可能稍有不同,但很相似,整张图片共享特征检测器,提取效果也很好。
第二个方法是使用稀疏连接
第二个方法是使用稀疏连接,我来解释下。这个0是通过3×3的卷积计算得到的,它只依赖于这个3×3的输入的单元格,右边这个输出单元(元素0)仅与36个输入特征中9个相连接。而且其它像素值都不会对输出产生任影响,这就是稀疏连接的概念(这个要搞清楚na,记住了)。
再举一个例子,这个输出(右边矩阵中红色标记的元素 30)仅仅依赖于这9个特征(左边矩阵红色方框标记的区域),看上去只有这9个输入特征与输出相连接,其它像素对输出没有任何影响。
神经网络可以通过这两种机制减少参数,以便我们用更小的训练集来训练它,从而预防过度拟合。
你们也可能听过,卷积神经网络善于捕捉平移不变。通过观察可以发现,向右移动两个像素,图片中的猫依然清晰可见,因为神经网络的卷积结构使得即使移动几个像素,这张图片依然具有非常相似的特征,应该属于同样的输出标记。
实际上,我们用同一个过滤器生成各层中,图片的所有像素值,希望网络通过自动学习变得更加健壮,以便更好地取得所期望的平移不变属性。
这就是卷积或卷积网络在计算机视觉任务中表现良好的原因。
最后,我们把这些层整合起来,看看如何训练这些网络。
比如我们要构建一个猫咪检测器,
我们有下面这个标记训练集,x表示一张图片,^y是二进制标记或某个重要标记。
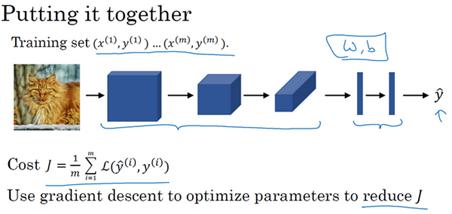
我们选定了一个卷积神经网络,输入图片,增加卷积层和池化层,然后添加全连接层,最后输出一个softmax,即^y。
卷积层和全连接层有不同的参数w和偏差b,我们可以用任何参数集合来定义代价函数。
一个类似于我们之前讲过的那种代价函数,并随机初始化其参数w和b,代价函数J等于神经网络对整个训练集的预测的损失总和再除以m
所以训练神经网络,你要做的就是使用梯度下降法,或其它算法,例如Momentum梯度下降法,含RMSProp或其它因子的梯度下降来优化神经网络中所有参数,以减少代价函数J的值。通过上述操作你可以构建一个高效的猫咪检测器或其它检测器。
你已经学习了卷积神经网络的所有基本构造模块,以及如何在高效图片识别系统中整合这些模块。
下周,我们将继续深入学习卷积神经网络。我曾提到卷积神经网络中有很多超参数,下周,我打算具体展示一些最有效的卷积神经网络示例,你也可以尝试去判断哪些网络架构类型效率更高。人们通常的做法是将别人发现和发表在研究报告上的架构应用于自己的应用程序。下周看过更多具体的示例后,相信你会做的更好。此外,下星期我们也会深入分析卷积神经网络如此高效的原因,同时讲解一些新的计算机视觉应用程序,例如,对象检测和神经风格迁移以及如何利用这些算法创造新的艺术品形式。期待与您再次相遇!
3 ↩︎