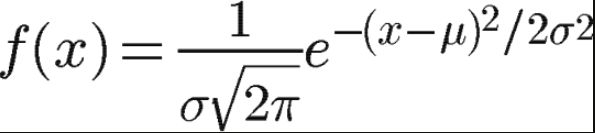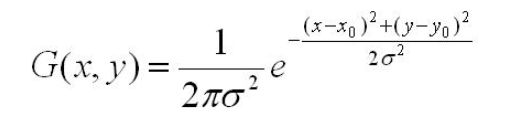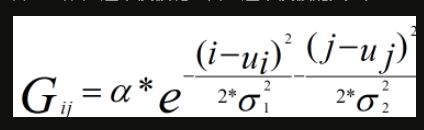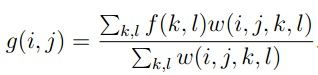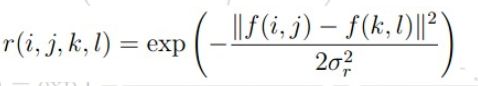opencv滤波及C++代码实现(高斯,中值,均值,双边)
图像平滑
图像平滑的目的之一是消除噪声,二是模糊图像。
从信号频谱的角度来看,信号缓慢变化的部分在频率域表现为低频,迅速变化的部分表现为高频。图像在获取、储存、处理、传输过程中,会受到电气系统和外界干扰而存在一定程度的噪声,图像噪声使图像模糊,甚至淹没图像特征,给分析带来困难。
滤波
分为 空间域滤波 和 频率域滤波
(1)空间域 指的是图像本身 直接对图像中的像素操作
(2)图像变换是将图像从空间域变换到某变换域(如 傅立叶变换中的频率域)的数学变换,在变换域 中进行处理,然后通过反变换把处理结果返回到空间域。
(3)图像在空域上具有很强的相关性,借助于正交变 换可使在空域的复杂计算转换到频域后得到简化
(4)借助于频域特性的分析,将更有利于获得图像的 各种特性和进行特殊处理
图像的空域滤波无非两种情况,线性滤波和非线性滤波。
滤波的意思就是对原图像的每个像素周围一定范围内的像素进行运算,运算的范围就称为掩膜。而运算就分两种了,如果运算只是对各像素灰度值进行简单处理(如乘一个权值)最后求和,就称为线性滤波;
而如果对像素灰度值的运算比较复杂,而不是最后求和的简单运算,则是非线性滤波;如求一个像素周围3x3范围内最大值、最小值、中值、均值等操作都不是简单的加权,都属于非线性滤波。
常见的线性滤波有:均值滤波、高斯滤波、盒子滤波、拉普拉斯滤波等等,通常线性滤波器之间只是模版系数不同。
非线性滤波利用原始图像跟模版之间的一种逻辑关系得到结果,如最值滤波器,中值滤波器和双边滤波器等。
一、下面先介绍均值滤波和高斯滤波
均值滤波:顾名思义就是求均值
均值滤波opencv C++API:blur(src,dst,Size ksize,Point anchor = Point(-1,-1),int borderType = BORDER_DEFAULT);
(1) src:输入图像,(2)dst:输出图像,大小类型与输入图像相同(3)ksize:模糊化的核大小(4)anchor:锚(mao)点,锚点为核中心。(5)像素外推法边缘的类型。 如: blur(src, dst, Size(3, 3));
高斯滤波:求高斯卷积核,然后卷积
一维高斯函数:
其中,μ是x的均值,σ是x的方差。因为计算平均值的时候,中心点就是原点,所以μ等于0。
二维高斯滤波公式:
1. 一维二维高斯函数中μ是服从正态分布的随机变量的均值,称为期望或均值影响正态分布的位置,实际的图像处理应用中一般取μ=0;σ是标准差,σ^2是随机变量的方差,σ定义了正态分布数据的离散程度,σ越大,数据分布越分散,σ越小,数据分布越集中。
在图形或滤波效果上表现为:σ越大,曲线越扁平,高斯滤波器的频带就越宽,平滑程度就越好,σ越小,曲线越瘦高,高斯滤波的频带就越窄,平滑程度也越弱;
2. 二维高斯函数具有旋转对称性,即滤波器在各个方向上的平滑程度是相同的.一般来说,一幅图像的边缘方向是事先不知道的,因此,在滤波前是无法确定一个方向上比另一方向上需要更多的平滑.旋转对称性意味着高斯平滑滤波器在后续边缘检测中不会偏向任一方向;
3. 高斯函数是单值函数。这表明,高斯滤波器用像素邻域的加权均值来代替该点的像素值,而每一邻域像素点权值是随该点与中心点的距离单调增减的。这一性质是很重要的,因为边缘是一种图像局部特征,如果平滑运算对离算子中心很远的像素点仍然有很大作用,则平滑运算会使图像失真;
4. 相同条件下,高斯卷积核的尺寸越大,图像的平滑效果越好,表现为图像越模糊,同时图像细节丢失的越多;尺寸越小,平滑效果越弱,图像细节丢失越少;
高斯滤波详解请看:https://www.cnblogs.com/invisible2/p/9177018.html
高斯滤波opencv C++API:
CV_EXPORTS_W void GaussianBlur( InputArray src, OutputArray dst, Size ksize,
double sigmaX, double sigmaY = 0,
int borderType = BORDER_DEFAULT ); InputArray src-----源图像
OutputArray dst-----目标图像
Size ksize----高斯内核大小,其中ksize.width和ksize.height可以不同,但是必须为正数和奇数,也可为零,均有sigma计算而来。
double sigmaX----表示高斯函数在X方向的标准偏差
double sigmaY---- 表示高斯函数在Y方向的标准偏差
若sigma为零,就将它设为sigmaX,如果两者均为零,就由ksize.width
和ksize.height计算出来。
int borderType -----用于推断图像外部像素的某种边界模式。
默认值 BORDER_DEFAULT C++代码表示均值滤波和高斯滤波:
// OpencvLvBo.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include
#include
#include
#include
#include
using namespace cv;
using namespace std;
void MeanFilter_my1(const Mat &src, Mat &dst, int ksize) //均值滤波 Scr 为要处理的图像,dst为目标图像,Ksize为卷积核的尺寸,卷积核的尺寸一般为 奇数
{
CV_Assert(ksize % 2 == 1); // 不满足这个条件,则返回一个错误。
int *kernel = new int[ksize*ksize]; // 卷积核的大小
for (int i = 0; i < ksize*ksize; i++) // 均值滤波所以都为1
kernel[i] = 1;
Mat tmp;
int len = ksize / 2;
tmp.create(Size(src.cols + len, src.rows + len), src.type()); //添加边框
dst.create(Size(src.cols, src.rows), src.type());
int channel = src.channels();
uchar *ps = src.data;
uchar *pt = tmp.data;
//添加边框是为了让图片周围的ksize/2 的像素都能进行均值滤波,若Ksize为3,,若是图片左上角的那个元素进行均值滤波,其实求的平均是 三个数(右、下、右下)的平均值。
for (int row = 0; row < tmp.rows; row++)//添加边框的过程
{
for (int col = 0; col < tmp.cols; col++)
{
for (int c = 0; c < channel; c++)
{
if (row >= len && row < tmp.rows - len && col >= len && col < tmp.cols - len)
pt[(tmp.cols * row + col)*channel + c] = ps[(src.cols * (row - len) + col - len) * channel + c];
else
pt[(tmp.cols * row + col)*channel + c] = 0;
}
}
}
uchar *pd = dst.data;
pt = tmp.data;
for (int row = len; row < tmp.rows - len; row++)//卷积的过程
{
for (int col = len; col < tmp.cols - len; col++)
{
for (int c = 0; c < channel; c++)
{
short t = 0;
for (int x = -len; x <= len; x++)
{
for (int y = -len; y <= len; y++)
{
t += kernel[(len + x) * ksize + y + len] * pt[((row + x) * tmp.cols + col + y) * channel + c];
}
}
pd[(dst.cols * (row - len) + col - len) * channel + c] = saturate_cast (t / (ksize*ksize));//防止数据溢出ushort是16为数据
}
}
}
delete[] kernel; // 释放 new 的卷积和空间
}
//方差可调节的高斯滤波
void GaussFilter_my(const Mat &src, Mat &dst, int ksize, double sigmaX, double sigmaY = 0)
{
CV_Assert(ksize % 2 == 1);
if (fabs(sigmaY) < 1e-5) // 传方差可调的高斯滤波。
sigmaY = sigmaX;
double *kernel = new double[ksize*ksize];
int center = ksize / 2;
double sum = 0;
for (int i = 0; i < ksize; i++)
{
for (int j = 0; j < ksize; j++)
{
//方差不可调的意思。
kernel[i * ksize + j] = exp(-(i - center)*(i - center) / (2 * sigmaX*sigmaX) - (j - center)*(j - center) / (2 * sigmaY*sigmaY));
// exp(x) 为 e^x e的x次幂 ,其实不为啥,没有除以 2πsigax^2;哪位大神看到,给解释一下。
sum += kernel[i*ksize + j];
}
}
for (int i = 0; i < ksize; i++)
{
for (int j = 0; j < ksize; j++)
{
kernel[i*ksize + j] /= sum; //进行归一化,核中各元素之和为1.
}
}
Mat tmp;
int len = ksize / 2;
tmp.create(Size(src.cols + len, src.rows + len), src.type()); //添加边框
dst.create(Size(src.cols, src.rows), src.type());
int channel = src.channels();
uchar *ps = src.data;
uchar *pt = tmp.data;
// 添加边框已经解释过了
for (int row = 0; row < tmp.rows; row++)//添加边框的过程
{
for (int col = 0; col < tmp.cols; col++)
{
for (int c = 0; c < channel; c++)
{
if (row >= len && row < tmp.rows - len && col >= len && col < tmp.cols - len)
pt[(tmp.cols * row + col)*channel + c] = ps[(src.cols * (row - len) + col - len) * channel + c];
else
pt[(tmp.cols * row + col)*channel + c] = 0;
}
}
}
uchar *pd = dst.data;
pt = tmp.data;
// 卷积不懂看我博客掩膜那篇博客。
for (int row = len; row < tmp.rows - len; row++)//卷积的过程
{
for (int col = len; col < tmp.cols - len; col++)
{
for (int c = 0; c < channel; c++)
{
short t = 0;
for (int x = -len; x <= len; x++)
{
for (int y = -len; y <= len; y++)
{
t += kernel[(len + x) * ksize + y + len] * pt[((row + x) * tmp.cols + col + y) * channel + c];
}
}
pd[(dst.cols * (row - len) + col - len) * channel + c] = saturate_cast (t); //防止数据溢出ushort是16为数据
}
}
}
delete[] kernel;
}
int main()
{
Mat src = imread("C://Users//Geek//Desktop//1281425_2019-07-18_10_0//hua.jpg");
//Mat img = imread("E://heibai.jpg");
//imshow("img", img);
imshow("dst", src);
Mat dst = Mat::zeros(src.size(), src.type());
int k = 7;
double sigmaX = 0.001;
double sigmaY = 0.001;
MeanFilter_my1(src, dst, k);
imshow("dst1", dst);
GaussFilter_my(src, dst, k, sigmaX, sigmaY);
imshow("dst2", dst);
waitKey(0);
}
二、中值滤波
中值滤波是一种非线性滤波,它能在滤除噪声的同时很好的保持图像边缘
中值滤波的原理:把以当前像素为中心的小窗口内的所有像素的灰度按从小到大排序,取排序结果的中间值作为该像素的灰度值
中值滤波,在这就不进行代码演示了
opencv C++ API medianBlur(src, dst,int Kisze ); 如: medianBlur(src, dst, 5); Ksize 为大于1的奇数。
三、双边滤波
双边滤波(Bilateral Filter)是非线性滤波中的一种。这是一种结合图像的空间邻近度与像素值相似度的处理办法。在滤波时,该滤波方法同时考虑空间临近信息与颜色相似信息,在滤除噪声、平滑图像的同时,又做到边缘保存。
双边滤波采用了两个高斯滤波的结合。一个负责计算空间邻近度的权值,也就是常用的高斯滤波器原理。而另一个负责计算像素值相似度的权值。在两个高斯滤波的同时作用下,就是双边滤波。
双边滤波的基本思想是:将高斯滤波(空间临近)的原理中,通过各个点到中心点的空间临近度计算的各个权值进行优化,将其优化为空间临近度计算的权值 和 像素值相似度计算的权值的乘积,优化后的权值再与图像作卷积运算。从而达到保边去噪的效果。
(1)双边滤波的公式:
其中 g(i, j)代表输出点;
f(k, l)代表(多个)输入点;
w(i, j, k, l)代表经过两个高斯函数计算出的值(这里还不是权值)
权重系数w(i,j,k,l)取决于定义域核
和值域核
的乘积
(2) opencv实现
cvSmooth(m_iplImg, dstImg, CV_BILATERAL, 2 * r + 1, 0, sigma_r, sigma_d); // 平滑处理 第一种
bilateralFilter(Mat &src, Mat &dst,int d , double sigmaColor, double sigmaSpace); 双边滤波器可以去除无关噪声,同时保持较好的边缘信息。
但是,其速度比绝大多数滤波器都慢。
关于双边滤波,可以参考:Bilateral Filter
关于2个sigma参数:
简单起见,可以令2个sigma的值相等;
如果他们很小(小于10),那么滤波器几乎没有什么效果;
如果他们很大(大于150),那么滤波器的效果会很强,使图像显得非常卡通化;
关于参数d:
过大的滤波器(d>5)执行效率低。
对于实时应用,建议取d=5;
对于需要过滤严重噪声的离线应用,可取d=9;
d>0时,由d指定邻域直径;
d<=0时,d会自动由sigmaSpace的值确定,且d与sigmaSpace成正比;
(3) c++实现
// opencvBilateralfilter.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
//#include
#include
#include
#include
#include
#include"opencv2/imgproc/imgproc.hpp"
#include // 双边高斯滤波的头文件。
#include
#include
using namespace cv;
using namespace std;
/* 计算空间权值 */ // 高斯空间
double **get_space_Array(int _size, int channels, double sigmas)
{
// [1] 空间权值
int i, j;
// [1-1] 初始化数组
double **_spaceArray = new double*[_size + 1]; //多一行,最后一行的第一个数据放总值
for (i = 0; i < _size + 1; i++) {
_spaceArray[i] = new double[_size + 1];
}
// [1-2] 高斯分布计算
int center_i, center_j;
center_i = center_j = _size / 2;
_spaceArray[_size][0] = 0.0f;
// [1-3] 高斯函数
for (i = 0; i < _size; i++) {
for (j = 0; j < _size; j++) {
_spaceArray[i][j] =
exp(-(1.0f)* (((i - center_i)*(i - center_i) + (j - center_j)*(j - center_j)) /
(2.0f*sigmas*sigmas)));
_spaceArray[_size][0] += _spaceArray[i][j];
}
}
return _spaceArray;
}
/* 计算相似度权值 */ // 像素点相似度。
double *get_color_Array(int _size, int channels, double sigmar)
{
// [2] 相似度权值
int n;
double *_colorArray = new double[255 * channels + 2]; //最后一位放总值
double wr = 0.0f;
_colorArray[255 * channels + 1] = 0.0f;
for (n = 0; n < 255 * channels + 1; n++) {
_colorArray[n] = exp((-1.0f*(n*n)) / (2.0f*sigmar*sigmar));
_colorArray[255 * channels + 1] += _colorArray[n];
}
return _colorArray;
}
/* 双边 扫描计算 */ // 三通道一起影响像素点相似度。
void doBialteral(cv::Mat *_src, int N, double *_colorArray, double **_spaceArray)
{
int _size = (2 * N + 1);
cv::Mat temp = (*_src).clone();
// [1] 扫描
for (int i = 0; i < (*_src).rows; i++) {
for (int j = 0; j < (*_src).cols; j++) {
// [2] 忽略边缘
if (i >(_size / 2) - 1 && j >(_size / 2) - 1 &&
i < (*_src).rows - (_size / 2) && j < (*_src).cols - (_size / 2)) {
// [3] 找到图像输入点,以输入点为中心与核中心对齐
// 核心为中心参考点 卷积算子=>高斯矩阵180度转向计算
// x y 代表卷积核的权值坐标 i j 代表图像输入点坐标
// 卷积算子 (f*g)(i,j) = f(i-k,j-l)g(k,l) f代表图像输入 g代表核
// 带入核参考点 (f*g)(i,j) = f(i-(k-ai), j-(l-aj))g(k,l) ai,aj 核参考点
// 加权求和 注意:核的坐标以左上0,0起点
double sum[3] = { 0.0,0.0,0.0 };
int x, y, values;
double space_color_sum = 0.0f;
// 注意: 公式后面的点都在核大小的范围里
// 双边公式 g(ij) = (f1*m1 + f2*m2 + ... + fn*mn) / (m1 + m2 + ... + mn)
// space_color_sum = (m1 + m12 + ... + mn)
for (int k = 0; k < _size; k++) {
for (int l = 0; l < _size; l++) {
x = i - k + (_size / 2); // 原图x (x,y)是输入点
y = j - l + (_size / 2); // 原图y (i,j)是当前输出点
values = abs((*_src).at(i, j)[0] + (*_src).at(i, j)[1] + (*_src).at(i, j)[2]
- (*_src).at(x, y)[0] - (*_src).at(x, y)[1] - (*_src).at(x, y)[2]);
space_color_sum += (_colorArray[values] * _spaceArray[k][l]); // _colorArray[values] * _spaceArray[k][l] 这个就是m1、m2...
// 可以发现 这里的(x,y)和 (k,j)在卷积和位置上,并没有对应(差不多为中心对称),这时候我觉着应该有疑惑,为什么不是对应点的像素相似度*对应点的 高斯空间卷积核呢?
//空间高斯滤波卷积核,由公式可以发现,只要到卷积核中心点距离一样的点, _spaceArray[][] 都一样。 ---- ①
}
}
// 计算过程
for (int k = 0; k < _size; k++) {
for (int l = 0; l < _size; l++) {
x = i - k + (_size / 2); // 原图x (x,y)是输入点
y = j - l + (_size / 2); // 原图y (i,j)是当前输出点
values = abs((*_src).at(i, j)[0] + (*_src).at(i, j)[1] + (*_src).at(i, j)[2]
- (*_src).at(x, y)[0] - (*_src).at(x, y)[1] - (*_src).at(x, y)[2]);
for (int c = 0; c < 3; c++) {
sum[c] += ((*_src).at(x, y)[c] * _colorArray[values]* _spaceArray[k][l]) / space_color_sum;
// 这个是 卷积核内某一个像素的当前通道的值 乘以 归一化的卷积和
// 归一化的卷积和是: 核膜区域内的对应的像素的所有通道的相似度 * 对应(似于)当前点高斯空间上的卷积核(不懂的看①) 然后除以 总数,进行归一化。
// sum[] 为长度为3的数组,对应输出点 3个通道的像素值。
}
}
}
for (int c = 0; c < 3; c++) {
temp.at(i, j)[c] = sum[c]; // 不知道这个sum[] 中的数 会不会超 255,这里没有控制,不放心的小伙伴可以控制一下。
}
}
}
}
// 放入原图
(*_src) = temp.clone();
return;
}
//想使用uchar * date = (*src).ptr(i); ptr 只能获取第i行的指针。
// 算的时候 一个通道中相互影响的双边滤波
void doBialteral_dan(cv::Mat *_src, int N, double *_colorArray, double **_spaceArray)
{
int size = 2 * N + 1;
Mat dst = (*_src).clone();
for (int i = 0; i < (*_src).rows; i++){
const uchar *current = (*_src).ptr(i); // 使用 ptr 指针的方法获取像素点,应该只能获取行指针。
for (int j = 0; j < (*_src).cols; j++){
if (i < N || j < N || (*_src).rows - i <= N || (*_src).cols - j <= N)
continue;
//double sum[3] = { 0 };
for (int c = 0; c < (*_src).channels(); c++){
double weight_quan = 0, eve_weigth = 0;
for (int k = -N; k <= N; k++){
for (int l = -N; l <= N; l++) {
const uchar *current1 = (*_src).ptr(i+k);
int Color_dif = (int)abs(current[j* (*_src).channels() +c] - current1[(j + l)*(*_src).channels() + c]);
double recom_weigth = _spaceArray[k + N][l + N] * _colorArray[Color_dif]; //每一个通道点值的符合权重
eve_weigth += _src->ptr(i+k)[(j+l)*(*_src).channels()+c] * recom_weigth;
weight_quan += recom_weigth;
}
}
// 每个像素点 一个通道一个通道的算。
dst.ptr(i)[j * (dst).channels() + c] = (uchar)(eve_weigth / weight_quan);
}
}
}
(*_src) = dst.clone();
return;
}
/* 双边滤波函数 */
void myBialteralFilter(cv::Mat *src, cv::Mat *dst, int N, double sigmas, double sigmar)
{
// [1] 初始化
*dst = (*src).clone();
int _size = 2 * N + 1;
// [2] 分别计算空间权值和相似度权值
int channels = (*dst).channels();
double *_colorArray = NULL;
double **_spaceArray = NULL;
_colorArray = get_color_Array(_size, channels, sigmar);
_spaceArray = get_space_Array(_size, channels, sigmas);
// [3] 滤波
//doBialteral(dst, N, _colorArray, _spaceArray); // ---- 三通道一起算像素相似度
doBialteral_dan(dst, N, _colorArray, _spaceArray); // ---- 单通道 一个通道一个通道的算 像素相似度。
return;
}
int main()
{
// [1] src读入图片
cv::Mat src = cv::imread("C:\\Users\\Geek\\Desktop\\1281425_2019-07-18_10_0\\youbantu.jpg");
// [2] dst目标图片
cv::Mat dst;
// [3] 滤波 N越大越平越模糊(2*N+1) sigmas空间越大越模糊sigmar相似因子
myBialteralFilter(&src, &dst, 10, 12.5, 50); // --- 自己写的,两个方法,耗时都长,但是模糊效果好。
//bilateralFilter(src, dst, 25, 12.5, 50); // opencv自带的函数,耗时短,模糊效果不好。
// [4] 窗体显示
cv::imshow("src 1006534767", src);
cv::imshow("dst 1006534767", dst);
cv::waitKey(0);
cv::destroyAllWindows();
return 0;
}
自己写的双边滤波,太慢了,但是模糊效果真的不错。但是opencv自带的函数,是真的快,但是效果一般,下面是自己写的模糊效果图: