概率论基础知识（二） 随机变量及其分布

概率论基础知识（二） 随机变量及其分布

1、随机变量

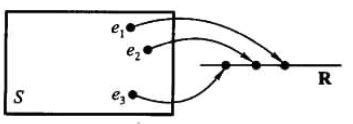
定义：设随机试验的样本空间为S={e}, X=X(e)是定义在样本空间S上的实值单值函数。称X=X(e)为随机变量。
这样一来，样本空间可以很好的映射到一系列的实值上，方便了接下来各种性质的讨论。

• 随机变量可以分为：离散型随机变量和非离散型随机变量，其中非离散型随机变量主要以连续型随机变量为主。
• 离散型随机变量：随机变量可能取到的值时有限个数或可列无限多个。$X=a_1,a_2,...$
• 连续型随机变量：随机变量可能取到的值时无限个数。$Y\in (a,b)$

2、随机变量的分布函数

定义：设X是一个随机变量，x是任意实数，函数$F(x)=P\{X\le x\}$称为X的分布函数，有时也记为X ~ F(x)。

对于任意实数$x_1,x_2(x_1<x_2)$，
$$P\{x_1<X\le x_2\}=P\{X\le x_2\}-P\{X\le x_1\}=F(x_2)-F(x_1)$$$$P\{X>x_1\}=1-P\{X\le x\}=1-F(x_1)$$ 因此，若已知X的分布函数，就可以知道X落在任一区间上的概率，在这个意义上说，分布函数完整地描述了随机变量的统计规律性。

如果将X看成是数轴上的随机点的坐标，那么，分布函数F(x)在x处的函数值就表示x落在区间$(-\infty ，x)$上的概率。

性质：（1）F(x)是不减函数;
    \,\;\qquad （2）$0\le F(x)\le 1$, 且 $F(-inf)=0,F(inf)=1$;
    \,\;\qquad （3）$F(x+0)=F(x)$，即F(x) 右连续

3、离散型随机变量及其分布律

分布律：对于离散型随机变量X，可以取的值有 $x_1,...,x_i,...,x_n$， 对应的概率为 $P(x_1),...,P(x_i),...,P(x_n)$。

常用离散型随机分布

（1）0-1分布
事件只有发生和不发生两种可能，发生的概率为p，则不发生的概率为（1-p），那么:
$$P\{X=k\}=p^k(1-p{)}^{1-k},k=0,1$$

（2）伯努利试验、二项分布
伯努利试验：一次试验只有两种可能结果：发生为A，不发生为$\overline{A}$，并且$P(A)=p,P(\overline{A})=1-p$，n次独立重复的伯努利试验服从二项分布：设k表示事件A发生的次数，则：
$$b(k;n,p)=P\{X=k\}=C_n^k{p}^k(1-p{)}^{n-k},k=0,1,...,n$$记为X~(n,p)，即X服从参数为n，p的二项分布。
注意：重复是指每次试验p不变；独立是指各次结果互不影响。

例：设子弹命中目标的概率为0.01，现发射500次，则击中目标的最可能次数是多少次？并求出相应的P。
解：
命中目标最可能次数是5次
$b(5;500,0.01)=C_{500}^5(0.01{)}^5(0.99{)}^{4}95=0.1176$
计算困难，方法：
（1）极限定理
（2）Poisson分布近似

注：

使b(k;n,p)取最大值的项b(m;n,p)叫中心项，m叫最可能成功次数。

（3）泊松分布
若随机变量x(x=k)只取零和正整数值0，1，2，…，且其概率分布为:
$$p(x=k)=\frac{{\lambda }^k}{k!}{e}^{-\lambda }，k=0,1,\dots \dots$$其中λ>0；e=2.7182…是自然对数的底数，则称x服从参数为λ的波松分布(Poisson’s distribution)，记为x～P(λ)。
波松分布作为一种离散型随机变量的概率分布有一个重要的特征：这就是它的平均数和方差相等，都等于常数λ，即$\mu ={\sigma }^2=\lambda$。利用这一特征， 可以初步判断一个离散型随机变量是否服从泊松分布。

为什么${\sum }_{k=0}^{\infty }\frac{{\lambda }^k}{k!}{e}^{-\lambda }=1$ ？
由泰勒展开式$e^x={\sum }_{k=0}^{\infty }\frac{x^k}{k!}$
${\sum }_{k=0}^{\infty }\frac{{\lambda }^k}{k!}{e}^{-\lambda }=e^{-\lambda }\cdot {\sum }_{k=0}^{\infty }\frac{{\lambda }^k}{k!}=e^{-\lambda }\cdot e^{\lambda }=1$

注：泊松分布的应用：
（1）作为二项分布的近似；
（2）服从Poisson分布的现象非常多（生活、物理学 …）
（3）“基本粒子” --> 用于构造其他分布

泊松定理：当二项分布的n很大而p很小时，泊松分布可作为二项分布的近似，其中λ为np。通常当n≧20,p≦0.05时，就可以用泊松公式近似得计算。事实上，泊松分布正是由二项分布推导而来的。

实际中很多事件服从泊松分布：一本书一页中的印刷错误数，某地区在一天内邮递遗失的信件数、某一医院在一天内的急诊病人数、某一地区一个时间间隔内发生交通事故的次数，在一个时间间隔内某种放射性物质发出的、经过计算机的粒子数等。
（可以发现这些例子中，都是小概率事件，从实际中与泊松定理联系起来。）

分赌本问题：
甲、乙两赌徒赌技相同，各出赌注100法郎，每局无平局。他们约定，谁先赢三局则得到全部200法郎的赌本。
当甲赢了2局，乙赢了1局时，因故要中止赌博。现问这200法郎如何分才算公平？

import random

def Bookie(n, n1, n2):
    for i in range(2*n-1-n1-n2):
        D = random.randint(1,2)
        if D == 1:
            n1 += 1
        else:
            n2 += 1

        if n == n1:
            return 1
        if n == n2:
            return 2

N = 10000
win = 0
for i in range(N):
    if Bookie(3, 2, 1) == 1:
        win += 1

print("甲赢得的概率为：%f" % (float(win)/float(N)))
print("乙赢得的概率为：%f" % (1 - float(win)/float(N)))

运算结果：

甲赢得的概率为：0.741100
乙赢得的概率为：0.258900

4、连续型随机变量及其概率密度

对于随机变量x，若存在一个非负的可积函数f(x)，使得对任意实数x，有$F(x)={\int }_{-\infty }^{x}f(t)dt$ 则称x为连续性随机变量。其中f(x)为x的概率分布密度函数，简称概率密度记为x ~ f(x)。

概率密度函数的积分，即围成的面积，为随机变量落入某一区间的概率，如图所示：

性质：
（1）$f(x)\ge 0,-\infty <x-<+\infty$
（2）${\int }_{-\infty }^{+\infty }f(t)dt=1$
（3）对任意$x_1\le x_2，P\{x_1<Z\le x_2\}={\int }_{x_1}^{x_2}f(t)dt=F(x_2)-F(x_1)$
（4）若f(x)在x点连续，则$F^{\prime }(x)=f(x)$
（5）改变f(x)在个别点处的函数值不影响F(x)
（6）对任意x，$P\{X=x\}={\int }_x^{x}f(t)dt=0$

约定：提到概率分布时，
\qquad\qquad 离散型 <–> 分布律；
\qquad\qquad 连续型 <–> 概率密度；

常见的三种连续性随机变量
（1）均匀分布
随机变量落入区间(a，b)中任意等长度的子区间内的可能性是相同的。或者说它落入(a，b)区间内的概率只依赖于子区间内的长度而与子区间的位置无关，表示为 X~U(a,b)。
$$P(x)=\{\begin{array}{ll}\frac{1}{b-a,}& \text{a < x < b}\\ 0,& \text{其它}\end{array}$$

均匀分布的概率密度：
$$P(x)=\{\begin{array}{ll}0,& \text{x < a}\\ \frac{x-a}{b-a,}& \text{a <= x < b}\\ 1,& \text{x >= b}\end{array}$$

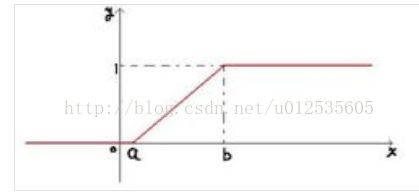
理解“均匀”的含义： 等可能性

（2）指数分布

其中λ > 0是分布的一个参数，常被称为率参数（rate parameter）。即每单位时间内发生某事件的次数。指数分布的区间是[0,∞)。 如果一个随机变量X呈指数分布，则可以写作：X ~ E(λ)。

在不同的教材有不同的写法，θ=1/λ,因此概率密度函数，分布函数和期望方差有两种写法。

其中θ>0为常数，则称X服从参数θ的指数分布。

指数分布的分布函数：

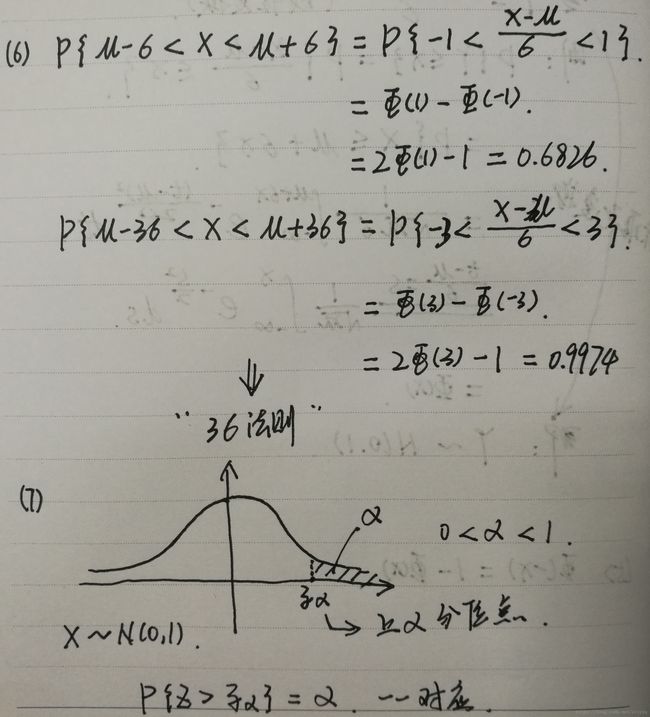
（3）正太分布 （高斯(Gauss)分布）
若随机变量 服从一个位置参数为$\mu$、尺度参数为$\sigma$的概率分布，且其概率密度函数为:

则这个随机变量就称为正态随机变量，正态随机变量服从的分布就称为正态分布，记作$XN(\mu ,{\sigma }^2)$，读作X服从$N(\mu ,{\sigma }^2)$，或X服从正态分布。
其中：正态分布的积分可以利用广义二重积分和极坐标。

高斯分布的不同参数的影响：

性质：

买面包问题：
·一个叫庞加莱的哥们每次买面包都回家称，并做记录，他发现他的面包一年的平均重量为0.95kg，于是他认为面包店缺斤少两，投诉了该面包店。
于是该面包店老板记住了庞加莱，叮嘱店员每次给他大的。
一年后，庞加莱又投诉面包店，说面包店继续缺斤少两，欺骗老百姓。只不过是每次故意给他大的面包。
庞加莱如何知道的？


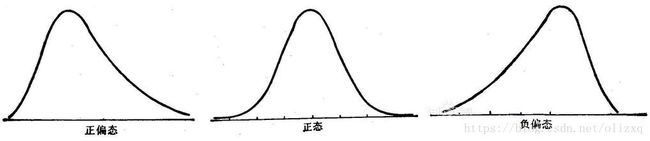
比较两次模拟结果输出的偏度值，明显第一次处于正态，第二次处于正偏态。

偏度（skewness），是统计数据分布偏斜方向和程度的度量，是统计数据分布非对称程度的数字特征。偏度(Skewness)亦称偏态、偏态系数。
表征概率分布密度曲线相对于平均值不对称程度的特征数。直观看来就是密度函数曲线尾部的相对长度。

• 正态分布的偏度为0，两侧尾部长度对称。若以bs表示偏度。
• bs<0称分布具有负偏离，也称左偏态，此时数据位于均值左边的比位于右边的少，直观表现为左边的尾部相对于与右边的尾部要长，因为有少数变量值很小，使曲线左侧尾部拖得很长；
• bs>0称分布具有正偏离，也称右偏态，此时数据位于均值右边的比位于左边的少，直观表现为右边的尾部相对于与左边的尾部要长，因为有少数变量值很大，使曲线右侧尾部拖得很长；
• bs接近0则可认为分布是对称的。若知道分布有可能在偏度上偏离正态分布时，可用偏离来检验分布的正态性。右偏时一般算术平均数>中位数>众数，左偏时相反，即众数>中位数>平均数。正态分布三者相等。
  

5、随机变量的函数的分布

随机变量X的函数Y=g(X)也是一个随机变量，可以根据X的分布率或概率密度求出Y的分布率或概率密度。