训练深度学习模型的小技巧
本文是B站李宏毅老师机器学习学习笔记。本文主要解决模型在不同训练阶段出现问题的解决方法。
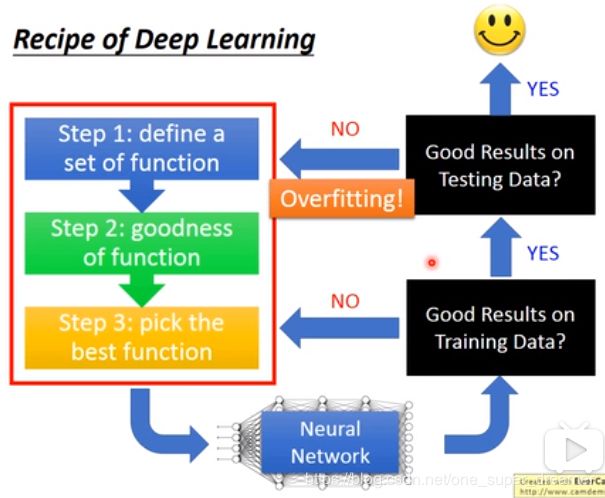
我们说的Deep Learning的三个步骤如下,但是模型在训练集和测试集上得到的结果不一定太好,如果是在训练集上得到的结果不理想,那么就是最后一步选择模型的时候出现问题;如果在训练集上良好,在测试集上结果不好,那就属于过拟合。
Recipe of Deep Learning
针对不同时间段出现问题的解决方法。
训练集上结果不好的解决方法
-
换一个新的激活函数
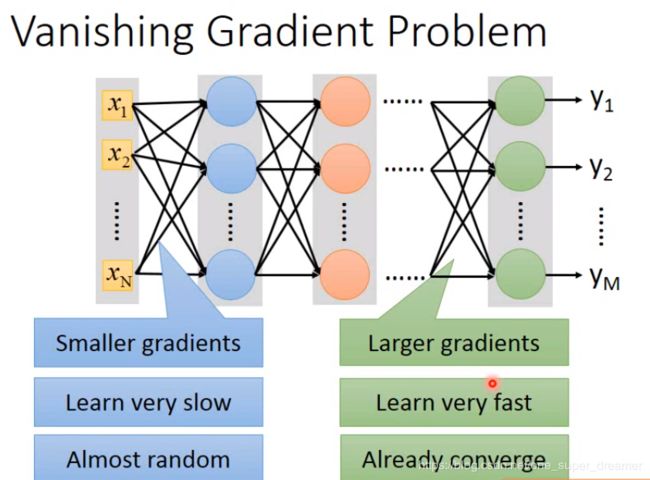
梯度消失问题(Vanishing Gradient)
当把网络结构构建的比较深的时候,网络前面部分(input layer)的参数对后面损失函数的微分是比较小的,而在网络输出的部分(output layer)微分是比较大的。当设定同样的Learning rate的时候,靠近input的地方参数的更新是比较慢的,靠近output的地方参数的更新是比较快的。出现这种情况正是Sigmoid导致的。
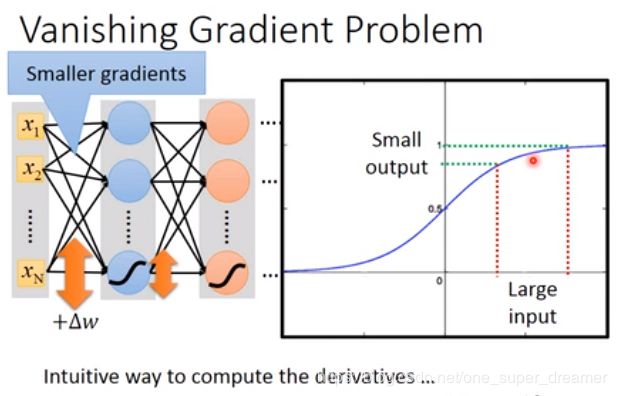
sigmod方法会将参数的变化变小,意思指的是假设输入有很大的变化,sigmod函数处理后变化比较小,这样如果有很多层网络,那么输入的变化对输出影响不大。我们可以测试在第一个layer 的某个参数加上W,看看对loss有什么影响。Sigmoid的函数图像如下图所示,它会将所有的值压缩到0-1之间,所以即使W有很大的变化,没通过一次Sigmoid就会衰减一次,网络结果越深,衰减次数越多,对output的影响就会越小。
所以解决训练集问题的方法之一是更换activation function。
可以将sigmod function换成ReLU
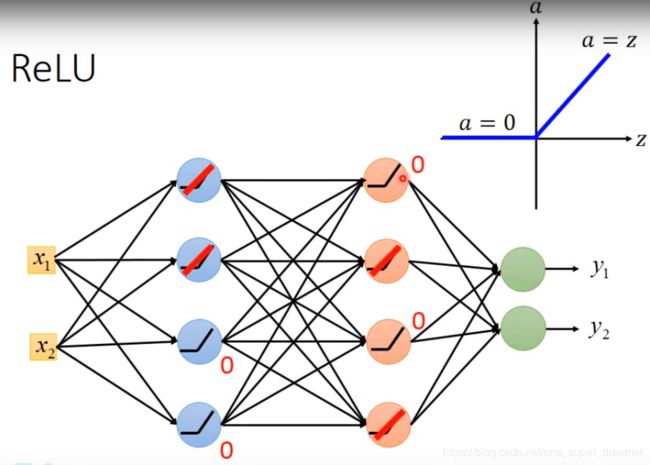
ReLU
ReLU图像中,Z时候激活函数的输入,a是激活函数的输出。如果输入大约0,则输出等于输入,否则输出为0。
它的优势有:1、它运算比较快。2、它可以解决梯度消失的问题
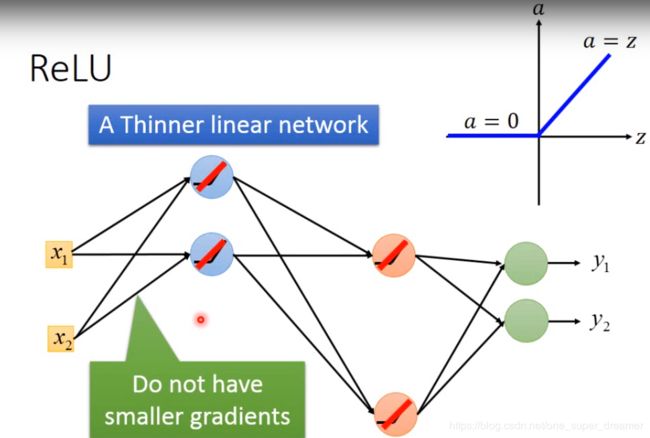
解决梯度消失的原因如下:它可以分为两部分,一部分是输出为0,另一部分是输出等于输入。
此时我们可以将输出为0的去掉得到下面的结果,此时剩下的是输入等于输出的线性网络。
有人可能会为那再转折点如何去微分,其实是不可能值正好在转折处,在左边区域是微分为0,在右边区域微分为1。
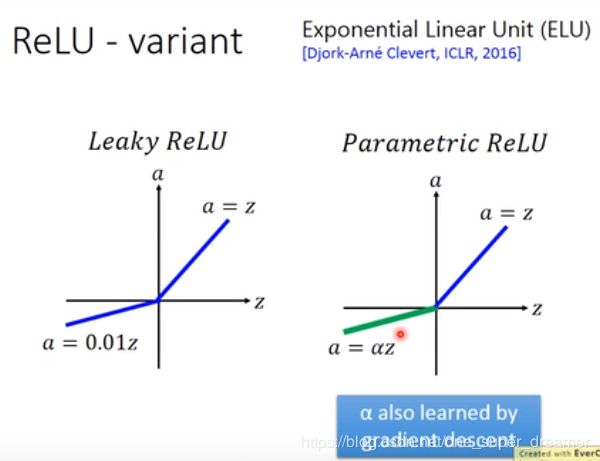
ReLU也可以有一些变化,如下图所示:
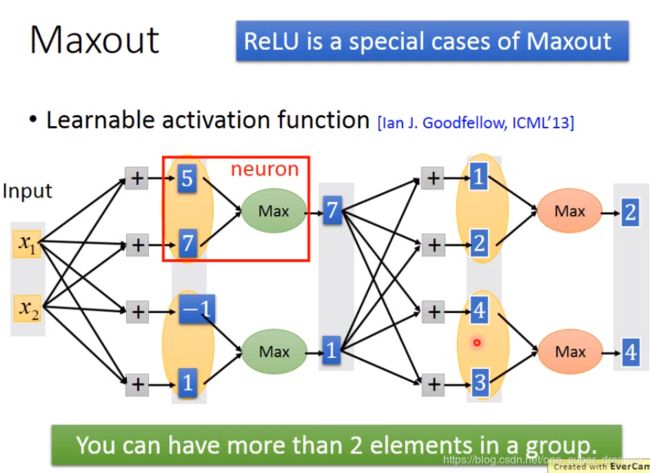
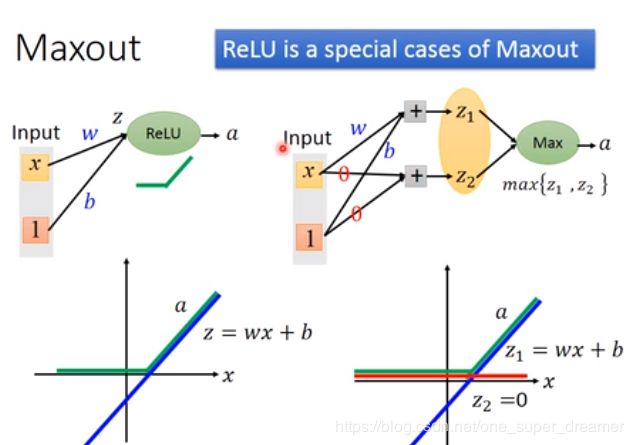
Maxout
在Maxout里面是让你的网络自动去学习出来激活函数,所以Maxout可以学习出ReLU,所以ReLU是Maxout 的一个特例。当然Maxout也可以学习出其他的激活函数。
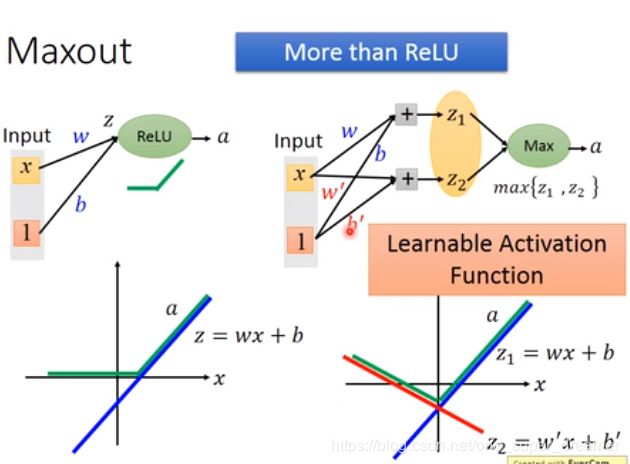
假设现在有输入x1,x2,它乘上不同的权重得到一些结果,现在在Maxout里面会把结果进行分组,哪些会分成一组是实现决定的,然后在同一个组里面选出最大的值当作输出。这过程就不加激活函数了,只是选择最大的。然后重复上述操作。在实际操作中你可以将多个放进一组,不一定非得要2个一组。
Maxout可以做出ReLU的效果。如下图Max在Z1和Z2中选择最大的就会跟ReLU一样。
Maxout也可以得到比ReLU更好的结果。
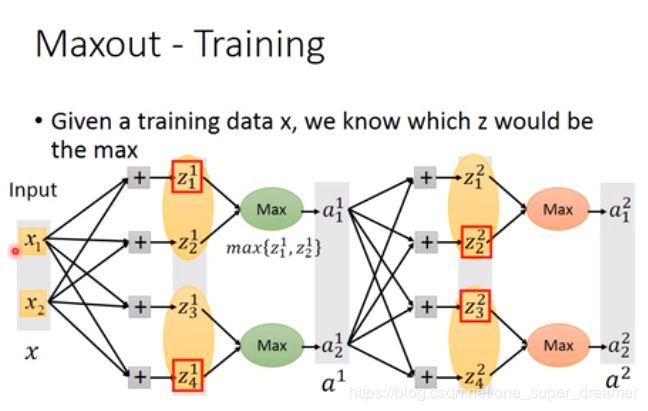
训练Maxout,假设现在红色框住的是比较大的部分,
-
Adaptive Learning Rate
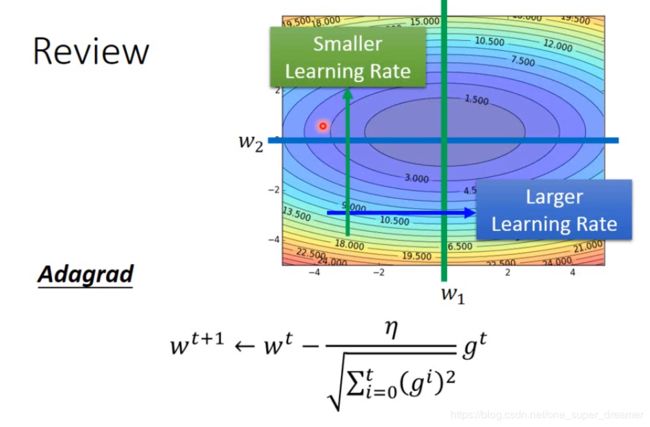
以前介绍的Adagrad在此回顾一下,下图中在蓝色方向平常梯度都是比较小的,所以给它比较大的Learning rate,在绿色箭头方向上平常梯度都是比较大的,所以给它比较小的Learning rate。将Learning rate带到下图中的式子进行更新参数。
但是在实际问题中可能遇到参数在不同区域的梯度是不一样的,所以需要进一步调整,如:RMSprop。它的参数变化如下图所示。
-
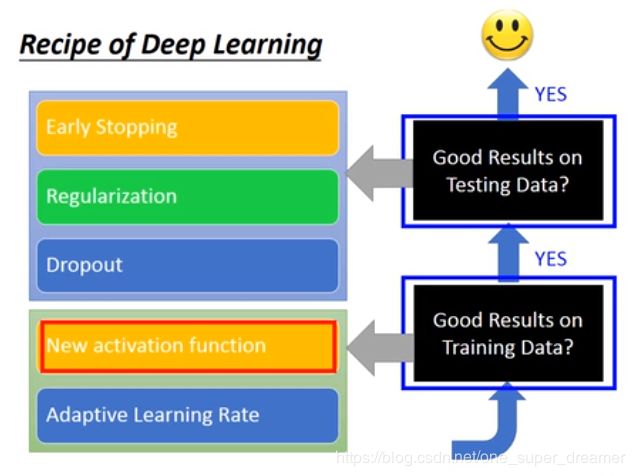
测试集上效果不好的解决方法
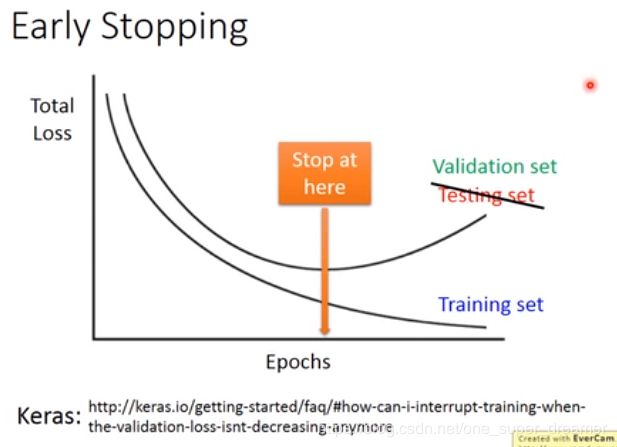
Early Stopping
由于训练和测试的分布有可能不一样,所以有可能在训练集上损失越来越小,在测试集上在变大,所以理想上就是应该停在一个两者都较小的地方。
Regularization
重新定义了要去最小化的损失函数。
梯度的变化,原来只是求个微分,现在的梯度加上了一个变化值。
sgn函数是取w正负号的意思,如果w是个正值,那么sgn(w)=+1,如果w是个负值,则sgn(w)=-1
L1和L2都是将参数接近于0,但是做法不同,L2是乘上一个小于1的值,L1 是减掉一个固定的值。
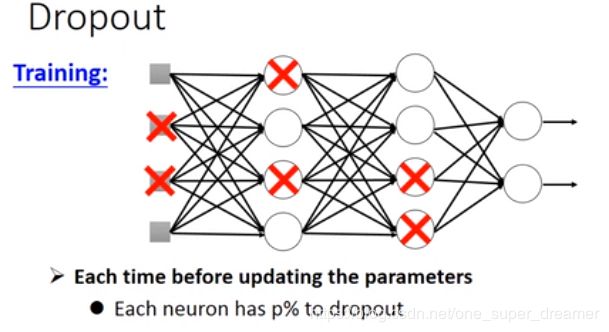
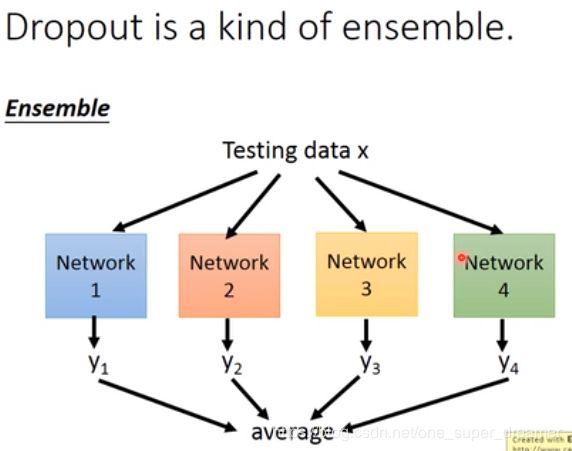
Dropout
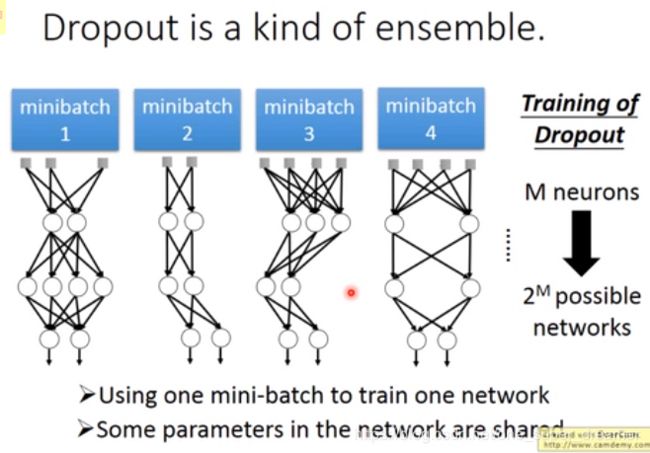
在开始训练之前先对网络中每一个神经元进行取样(sample),这个过程是要决定这个神经元要不要被丢掉,每个神经元有p%的概率被丢掉。当选中某一个被丢掉的时候,该神经元对应的权重也要被丢掉。
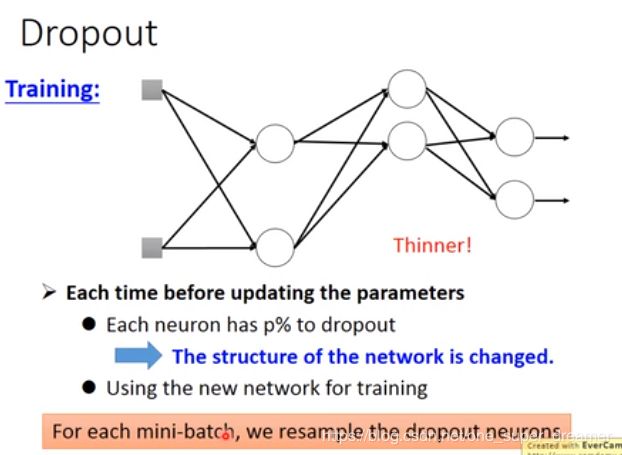
最后这个网络结构就会变的细长,然后再去对这个细长的网络进行训练。前面sample的方法在每一次更新参数之前都要执行,每次得到的结果都是不一样的。
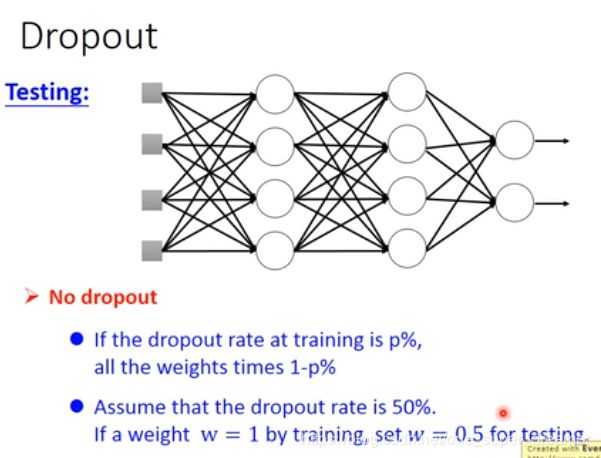
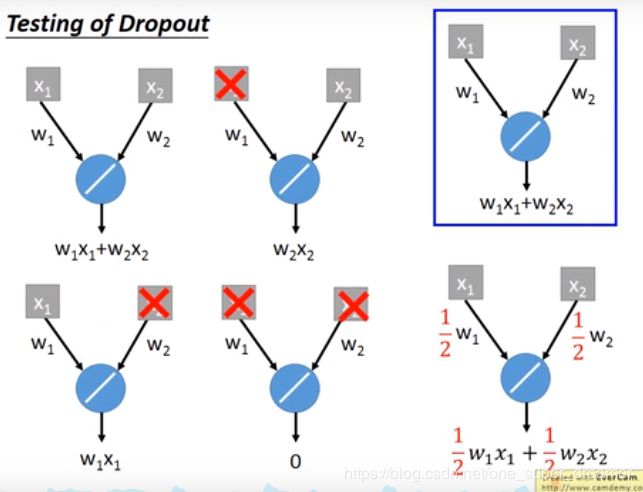
在测试的时候不做dropout,在训练的时候dropout rate是p%,那么在测试的时候每个权重都要乘以(1-p)%。
现在找一组最简单的网络结构来测试,以下共两个神经元,所以共2的2次方种情况,每一种情况出现的概率都是一样的。分别求出四种情况的结果,然后再求出平均值。
打红叉的代表该神经元被dropout掉了。