【搞定算法】单调栈问题:直方图中的最大矩形面积、求最大子矩阵的大小、可见山峰问题
目 录:
1、单调栈结构
1.1、单调栈结构的实现:无重复元素
1.2、单调栈结构的实现:有重复元素
2、单调栈结构的应用
2.1、直方图中的最大矩形面积
2.2、求最大子矩阵的大小
2.3、可见山峰问题
本文主要用于讲解一种在面试笔试中经常使用到的一种算法结构:单调栈结构。
1、单调栈结构
单调栈结构:给一个数组,求任何位置左边和右边离它最近的比它大/小的数。
要求:栈中元素需要满足单调性、单调递增/递减;
时间复杂度:O(N)
单调栈的工作过程:
1、新元素加入栈前,会在栈顶端把破坏栈单调性的元素都删除,直到栈为空或者栈满足单调性才能加入新元素;
2、单调栈是 O(N) 级的时间复杂度,所有元素只会进入栈一次,并且出栈后再也不会进栈;
3、单调栈可以找到元素向左遍历第一个比它小(大)的元素,也就是说在元素进栈前它向左拓展的区间已经确定,在出栈前它能向右拓展的区间也能确定(左区间好理解,仔细体会右区间的确定,若该元素至遍历结束后也未出栈,那么就是说在原数组中,该元素的右方向没有一个元素可以比它大/小,那么该元素的右边界就是原数组的大小(就是没有右边界),否则它的右边界就是令它出栈的元素)。
- 注意:单调栈分为两种情况:数据无重复和数据有重复的。
1.1、单调栈结构的实现:无重复元素
public class MonotonicStack {
/**
* 数组中午重复元素
* @param arr :数组
* @return res:每个位置上元素左边和右边离它最近的最小元素
*/
public static int[][] getNearLessNoRepeat(int[] arr){
if(arr == null || arr.length < 1){
return null;
}
// 两列:左边最小、右边最小
int[][] res = new int[arr.length][2];
Stack stack = new Stack<>();
for(int i = 0; i < arr.length; i++){
while(!stack.isEmpty() && arr[stack.peek()] > arr[i]){
// 如果当前数比栈顶元素小,则弹出栈中比arr[i]大的数,直到找到比它小的或者栈底
int popIndex = stack.pop();
// 当前弹出元素左边比它小的元素
int leftLessIndex = stack.isEmpty() ? -1 : stack.peek();
// 当前弹出元素右边比它小的元素:谁让它弹出的谁就是右边比它小的
int rightLessIndex = i;
res[popIndex][0] = leftLessIndex;
res[popIndex][1] = rightLessIndex;
}
// 找到正确位置,则将当前元素压入栈中
stack.push(i);
}
// for循环结束后,栈中还有元素
while(!stack.isEmpty()){
int popIndex = stack.pop();
int leftLessIndex = stack.isEmpty() ? -1 : stack.peek();
res[popIndex][0] = leftLessIndex;
// 右边不存在比它小的了
res[popIndex][1] = -1;
}
return res;
}
} 1.2、单调栈结构的实现:有重复元素
有重复元素时,只需要在每个位置拉一个链表出来就行了。每次插入元素都是插入到链表的尾部,这样任一元素左边比它小的最近的元素就是栈中左边位置链表的尾元素。
public class MonotonicStack {
/**
* 数组中有重复元素
* @param arr : 数组
* @return res:每个位置上元素左边和右边离它最近的最小元素
*/
public static int[][] getNearLess(int[] arr){
if(arr == null || arr.length < 1){
return null;
}
int[][] res = new int[arr.length][2];
Stack> stack = new Stack<>();
for(int i = 0; i < arr.length; i++){
while(!stack.isEmpty() && arr[stack.peek().getLast()] > arr[i]){
LinkedList pops = stack.pop();
for(int pop : pops){
//左边离它最近比它小的数的位置:是它压着的链表的最后一个
res[pop][0] = stack.isEmpty() ? -1 : stack.peek().getLast();
res[pop][1] = i;
}
}
// 把当前数的下标放进栈中(不要忘记判空)
if(!stack.isEmpty() && arr[stack.peek().getLast()] == arr[i]){
// 已经存在相同的值
stack.peek().addLast(i);
}else{
// 第一次碰到该值,直接拉个链表
LinkedList list = new LinkedList<>();
list.addLast(i);
stack.push(list);
}
}
// 如果全部数都遍历后,栈却不为空,说明栈中的数不存在右边比它小的数
// 只有右边数都比它大,才可以不出栈
while(!stack.isEmpty()){
LinkedList pops = stack.pop();
for(int pop : pops){
res[pop][0] = stack.isEmpty() ? -1 : stack.peek().getLast();
res[pop][1] = -1; // 右边不存在比它小的数了
}
}
return res;
}
}
2、单调栈结构的应用
2.1、直方图中的最大矩形面积
参考链接:https://blog.csdn.net/u012534831/article/details/74356851
问题:直方图是由排列在同一基线上的一系列矩形组成的多边形。为了简单起见,假设这些矩形的宽度相等但高度可能不同。例如,下图1给出了一个直方图,其中各个矩形的高度为3、2、5、6、1、4、4,宽度为标准1单位。当给定了一个保存所有矩形高度的数组时,如何找到其中最大的矩形。
对于给定的例子,最大矩形如图阴影部分所示:
- 思路:
考虑必须包含某个柱子的矩形的最大面积,那么我们就需要找到这个柱子往左和往右的边界,这样宽度高度都有了,就有了必须包含这个柱子的最大面积,左右柱子的这个最大面积求出来,这其中的最大即为全局最大。
- 算法步骤:
1、使用一个stack,首先压入第一个元素的位置,然后遍历数组,在遇到当前数组大于栈顶对应值时,直接入栈即可,否则进行出栈操作,直到栈顶元素的值小于当前元素。然后压入当前元素。这一过程中即可求出必须包含栈顶元素的最大矩阵面积。
2、遍历结束后如果栈中还有元素,也需要将其弹出,并计算。
- 算法原理:
假设现在遍历到 i,如果栈顶元素小于 heights[i],表明这个 i 就是栈顶元素的左边界,而栈顶元素的右边界就是栈顶元素的下边一个元素(为空补 -1),这样就可以求得必须包含栈顶元素的最大矩形面积。这样遍历一次之后就所有的情况都考虑到了。需要注意的是你遍历结束之后,可能栈中还有元素,也需要把这些元素弹出结算,此时这些元素的右边界即为heights.length。
public class LargestRetangleArea {
public static int largestRectangleArea(int[] heights){
if(heights == null || heights.length == 0){
return 0;
}
int res = 0;
Stack stack = new Stack<>();
for(int i = 0; i < heights.length; i++){
// 注意这里的等号 >= 最后一个相等的元素会计算出正确的值
while(!stack.isEmpty() && heights[stack.peek()] >= heights[i]){
int current = stack.pop();
// 结算当前元素的左右最近比它小的元素信息
int leftLessIndex = stack.isEmpty() ? -1 : stack.peek();
// 以当前元素为矩形高度时的总面积
int area = (i - leftLessIndex - 1) * heights[current];
// 更新最大面积
res = Math.max(res, area);
}
stack.push(i);
}
while(!stack.isEmpty()){
int current = stack.pop();
int leftLessIndex = stack.isEmpty() ? -1 : stack.peek();
int area = (heights.length - leftLessIndex - 1) * heights[current];
res = Math.max(res, area);
}
return res;
}
}
2.2、求最大子矩阵的大小
题目:给定一个整型矩阵 map,其中的值只有 0 和 1 两种,求其中全是 1 的所有矩形区域中,最大的矩形区域为 1 的数量。
例如:
1 1 1 0
其中,最大的矩形区域有 3 个 1,所以返回 3。
再如:
1 0 1 1
1 1 1 1
1 1 1 0
其中,最大的矩形区域有 6 个 1,所以返回 6。
分析:如果有答案,它一定是以某一行为底。
- 对每一行:
1、算出必须以第 i 行作为底的情况下的直方图高度是多少【从当前位置出发,往上有多少个连续的 1】
2、算出该直方图的最大矩形面积:单调栈问题,只是多了个等号,用上面那种 list 来解决重复也可以,只是这种更简单【相等也会让栈弹出,那么以该值为底的最大矩形是让它弹出那个相等的说了算】
- 综合 N 行,求出总的最大矩形面积
public class MaxRectangelWith1 {
public static int maxRecSize(int[][] map){
if(map == null || map.length == 0 || map.length == 0){
return 0;
}
int maxArea = 0;
// 有多少列,就生成多大的长度
int[] heights = new int[map[0].length];
// 必须以第i行做底的情况下的直方图数组
for(int i = 0; i < map.length; i++){
for(int j = 0; j < map[0].length; j++){
// 如果当前位置为0,则直接置0,否则置1
heights[j] = map[i][j] == 0 ? 0 : heights[j] + 1;
}
// 得到直方图中的最大值(计算以每一行为底时的最大面积,最后取最大返回)
maxArea = Math.max(maxRecFromBottom(heights), maxArea);
}
return maxArea;
}
// heights代表直方图数组,返回其中最大的长方形面积,可能包含重复值
public static int maxRecFromBottom(int[] heights){
if(heights == null || heights.length == 0){
return 0;
}
int maxArea = 0;
Stack stack = new Stack<>();
for(int i = 0; i < heights.length; i++){
// = 相等的时候是是算错了,但最后一个会算对,所以没关系
while(!stack.isEmpty() && heights[stack.peek()] >= heights[i]){
int current = stack.pop();
int leftLessIndex = stack.isEmpty() ? -1 : stack.peek();
// 以当前heights[current]为高度的最大矩形面积
int curArea = (i - leftLessIndex - 1) * heights[current];
maxArea = Math.max(maxArea, curArea);
}
stack.push(i);
}
// 遍历完了,但是栈中还有元素,要单独结算,R->height.length
while(!stack.isEmpty()){
int current = stack.pop();
int leftLessIndex = stack.isEmpty() ? -1 : stack.peek();
int curArea = (heights.length - leftLessIndex - 1) * heights[current];
maxArea = Math.max(maxArea, curArea);
}
return maxArea;
}
public static void main(String[] args) {
int[][] map = { { 1, 0, 1, 1 }, { 1, 1, 1, 1 }, { 1, 1, 1, 0 }};
System.out.println(maxRecSize(map));
}
} 2.3、可见山峰问题
- 心得:问题思想需要理解,编程直接用公式即可,无重复时直接用,有重复时,加上重复元素直接的可见对数即可。
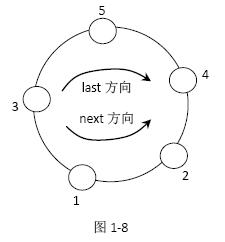
题目一个不含有负数的数组可以代表一圈环形山,每个位置的值代表山的高度。比如,{3,1,2,4,5}、{4,5,3,1,2}或{1,2,4,5,3}都代表同样结构的环形山。3->1->2->4->5->3 方向叫作next 方向(逆时针),3->5->4->2->1->3 方向叫作 last 方向(顺时针),如图所示。
山峰 A 和山峰 B 能够相互看见的条件为:
1.如果 A 和 B 是同一座山,认为不能相互看见。
2.如果 A 和 B 是不同的山,并且在环中相邻,认为可以相互看见。比如图1-8 中,相邻的山峰对有(1,2)(2,4)(4,5)(3,5)(1,3)。
3.如果 A 和 B 是不同的山,并且在环中不相邻,假设两座山高度的最小值为min。如果A通过next 方向到B 的途中没有高度比min 大的山峰,或者 A 通过last 方向到 B 的途中没有高度比 min 大的山峰,认为 A 和 B 可以相互看见。比如图中,高度为 3 的山和高度为 4 的山,两座山的高度最小值为 3。3 从 last 方向走向 4,中途会遇见 5,所以 last 方向走不通;3 从 next 方向走向4,中途会遇见1 和 2,但是都不大于两座山高度的最小值 3,所以 next 方向可以走通。
有一个能走通就认为可以相互看见。再如,高度为 2 的山和高度 为5 的山,两个方向上都走不通,所以不能相互看见。图中所有在环中不相邻,并且能看见的山峰对有(2,3)、(3,4)。给定一个不含有负数且没有重复值的数组 arr,请返回有多少对山峰能够相互看见。
进阶问题:给定一个不含有负数但可能含有重复值的数组 arr,返回有多少对山峰能够相互看见。
【要求】
如果 arr 长度为N,没有重复值的情况下时间复杂度达到 O(1),可能有重复值的情况下时间复杂度请达到 O(N)。
-
分析
原问题:时间复杂度 O(1) 的解。如果数组中所有的数字都不一样,可见山峰对的数量可以由简单公式得到。环形结构中只有1 座山峰时,可见山峰对的数量为 0;环形结构中只有2 座山峰时,可见山峰对的数量为1。这都是显而易见的。环形结构中有 i 座山峰时(i > 2),可见山峰对的数量为 2 × i - 3。下面给出证明。
我们只用高度小的山峰去找高度大的山峰,而永远不用高度大的山峰去找高度小的山峰【精髓】。比如题目描述中的例子,从 2 出发按照“小找大”原则,会找到 (2,3) 和 (2,4),但是不去尝试2能不能看到 1,因为这是“大找小”,而不是“小找大”。(1,2) 这一对可见山峰不会错过,因为从 1 出发按照“小找大”原则找的时候会找到这一对。从每一个位置出发,都按照“小找大”原则找到山峰对的数量,就是总的可见山峰对数量。
- 初级
环形结构中只有 1 座山峰时,可见山峰对的数量为0;环形结构中只有2座山峰时,可见山峰对的数量为 1。这都是显而易见易见的。
- 环形结构中有i座山峰时(i > 2),可见山峰对的数量为2 * i - 3。
因为 i 座山峰高度不一样,必然在环中存在唯一的最大值和唯一的次大值(第二大的值)。x 是除了最高值和次高值之外的任何一座山峰,所以 x 在 last 方向上必存在第一个高度比它大的节点,x 在 next 方向上也必存在第一个高度比它大的节点,所以从 x出发能找到且只能找到 2 对。
除了最大值和次大值之外还剩 i - 2 个节点,这 i - 2 个节点每一个都能找到 2 对,所以一共有(i - 2) * 2 对,还有 1 对,就是次大值能够看见最大值这对。所以一共是 2i - 3 对。
- 进阶:
1、首先遍历一次环形山结构,找到最大值的位置,如果最大值不只一个,找哪一个最大值都行。准备一个栈,栈中放 stack,Record 包含元素及元素目前重复了多少个;
2、求一个数左边(逆时针方向)离它最近的比它大的数,右边(顺时针)离它最近的比它大的数,然后他们就能和该数组成可见山峰对。栈中按从栈底到栈顶由大到小的顺序放入,不满足就弹出栈顶元素,说明找到了栈顶元素的可见山峰,然后计算可见山峰对;
- 可见山峰对 = 栈顶元素之间组成的(重复) + 栈顶元素和让它弹出的那个数 以及 栈顶元素压着的那个数 组成的可见山峰
- 弹出记录为(X, K),产生 C(2,K) + 2*K 对(公式,直接用即可)。
3、清算栈中剩下的
- 第一阶段: 栈里的元素大于两个,那么每弹出一个元素,则有 C(2, K) + 2 * K 对;
- 第二阶段: 栈里的元素等于 2 个: 那么弹出该元素,则有 C(2, K) + 最大值只有一个,那么不同高度组成的可见山峰只能一个一对,如果最大值有多个,则我每一个依然能找到 2 对可见山峰;
- 第三阶段: 只剩下最大值了,则可见山峰只能是在最大值之间 C(2, K);
public class GetVisiableNum {
public static class Record{
public int value;
public int times;
public Record(int value){
this.value = value;
this.times = 1;
}
}
public static int getVisiableNum(int[] arr){
if(arr == null || arr.length < 2){
return 0;
}
if(arr.length == 2){
return 1;
}
int size = arr.length;
int maxIndex = 0;
// 先在环中找到其中一个最大值的位置,哪一个都行
for(int i = 0; i < size; i++){
maxIndex = arr[i] > arr[maxIndex] ? i : maxIndex;
}
Stack stack = new Stack<>();
// 1、先把(最大值,1)这个记录放入stack中
stack.push(new Record(arr[maxIndex]));
// 2、从最大位置的下一个位置沿next方向遍历。当index再次回到maxIndex时,说了转了一圈,遍历结束
// 找到一个数左边(逆时针)方向离它最近比它大的数,右边(顺时针)离它最近比它大的数,这两个数就可以与该数组组成可见山峰对
int index = nextIndex(maxIndex, size);
int res = 0; // 可见山峰对数
while(index != maxIndex){
// 2.1 当前数字arr[index]要进栈,判断会不会破坏栈中元素从栈底到栈顶依次增大的顺序
// 如果破坏了,就依次弹出栈顶记录,并计算该数的可见山峰对数量
while(stack.peek().value < arr[index]){
// 弹出记录为(X,K),如果K==1,产生2对; 如果K>1,产生2*K + C(2,K)对。
// 【由于相同高度的山峰也是可见山峰,他们之间共有C(2,K)种组合,getInternalSum】
// 以及每个峰有左边最近比它大的和右边最近比它大的存在,即有两个可见山峰对,总共 2*times对
int times = stack.pop().times;
res += getInternalSum(times) + 2 * times;
}
// 2.2 当前数字arr[index]要进入栈了,如果和当前栈顶数字一样就合并,不一样就把记录(arr[index],1)放入栈中
if(stack.peek().value == arr[index]){
stack.peek().times++;
}else{
stack.push(new Record(arr[index]));
}
// 开始下一个数
index = nextIndex(index, size);
}
// 3、开始清理栈中的数据
// 第一阶段:栈里的元素大于两个,那么共 2*K + C(2,K)对
while(stack.size() > 2){
int times = stack.pop().times;
res += getInternalSum(times) + 2 * times;
}
// 第二阶段:栈里的元素等于2个
while(stack.size() == 2){
int times = stack.pop().times;
// 最大值有多个,则我每一个数依然能找到2对可见山峰
res += getInternalSum(times) + (stack.peek().times == 1 ? times : 2 * times);
}
// 第三阶段:栈里只有一个元素了
// 只剩下最大值了,则可见山峰只能是在最大值之间
res += getInternalSum(stack.pop().times);
return res;
}
// 如果k==1返回0,如果k>1返回C(2,k)
public static int getInternalSum(int k){
return k == 1 ? 0 : (k * (k - 1)) / 2;
}
// 环形数组中当前位置为i,数组长度为size,返回i的下一个位置
public static int nextIndex(int i, int size){
return i < (size - 1) ? (i + 1) : 0;
}
}