数据压缩算法—2无损压缩算法

几个常见的编码算法

（一） 字典算法

  字典算法是最为简单的压缩算法之一。它是把文本中出现频率比较多的单词或词汇组合做成一个对应的字典列表，并用特殊代码来表示这个单词或词汇。例如：
  有字典列表：
  00=Chinese
  01=People
  02=China
  源文本：I am a Chinese people,I am from China 压缩后的编码为：I am a 00 01,I am from 02。压缩编码后的长度显著缩小，这样的编码在SLG游戏等专有名词比较多的游戏中比较容易出现，比如《SD高达》。

（二） 固定位长算法（Fixed Bit Length Packing）

  这种算法是把文本用需要的最少的位来进行压缩编码。
  比如八个十六进制数：1，2，3，4，5，6，7，8。转换为二进制为：00000001，00000010，00000011，00000100，00000101，00000110，00000111，00001000。每个数只用到了低4位，而高4位没有用到（全为0），因此对低4位进行压缩编码后得到：0001，0010，0011，0100，0101，0110，0111，1000。然后补充为字节得到：00010010，00110100，01010110，01111000。所以原来的八个十六进制数缩短了一半，得到4个十六进制数：12，34，56，78。
  这也是比较常见的压缩算法之一。

（三） RLE算法

  这种压缩编码是一种变长的编码，RLE根据文本不同的具体情况会有不同的压缩编码变体与之相适应，以产生更大的压缩比率。
  变体1：重复次数+字符
文本字符串：A A A B B B C C C C D D D D，编码后得到：3 A 3 B 4 C 4 D。
  变体2：特殊字符+重复次数+字符
文本字符串：A A A A A B C C C C B C C C，编码后得到：B B 5 A B B 4 C B B 3 C。编码串的最开始说明特殊字符B，以后B后面跟着的数字就表示出重复的次数。
  变体3：把文本每个字节分组成块，每个字符最多重复 127 次。每个块以一个特殊字节开头。那个特殊字节的第 7 位如果被置位，那么剩下的7位数值就是后面的字符的重复次数。如果第 7 位没有被置位，那么剩下 7 位就是后面没有被压缩的字符的数量。例如：文本字符串：A A A A A B C D E F F F。编码后得到：85 A 4 B C D E 83 F（85H= 10000101B、4H= 00000100B、83H= 10000011B）
  以上3种不RLE变体是最常用的几种，其他还有很多很多变体算法，这些算法在Winzip Winrar这些软件中也是经常用到的。

（四） LZ77算法

  LZ77算法是由 Lempel-Ziv 在1977发明的，也是GBA内置的压缩算法。LZ77算法有许多派生算法(这里面包括 LZSS算法)。它们的算法原理上基本都相同，无论是哪种派生算法，LZ77算法总会包含一个滑动窗口（Sliding Window）和一个前向缓冲器（Read Ahead Buffer）。滑动窗口是个历史缓冲器，它被用来存放输入流的前n个字节的有关信息。一个滑动窗口的数据范围可以从 0K 到 64K，而LZSS算法使用了一个4K的滑动窗口。前向缓冲器是与滑动窗口相对应的，它被用来存放输入流的前n个字节，前向缓冲器的大小通常在0 – 258 之间。这个算法就是基于这些建立的。用下n个字节填充前向缓存器（这里的n是前向缓存器的大小）。在滑动窗口中寻找与前向缓冲器中的最匹配的数据，如果匹配的数据长度大于最小匹配长度 （通常取决于编码器，以及滑动窗口的大小，比如一个4K的滑动窗口，它的最小匹配长度就是2），那么就输出一对**〈长度（length），距离（distance）〉**数组。长度(length)是匹配的数据长度，而距离(distance)说明了在输入流中向后多少字节这个匹配数据可以被找到。
  LZ77压缩算法采用字典的方式进行压缩，是一个简单但十分高效的数据压缩算法。其方式就是把数据中一些可以组织成短语(最长字符)的字符加入字典，然后再有相同字符出现采用标记来代替字典中的短语，如此通过标记代替多数重复出现的方式以进行压缩。LZ77的主要算法逻辑就是，先通过前向缓冲区预读数据，然后再向滑动窗口移入（滑动窗口有一定的长度），不断的寻找能与字典中短语匹配的最长短语，然后通过标记符标记。
  
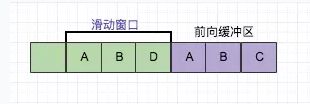
  目前从前向缓冲区中可以和滑动窗口中可以匹配的最长短语就是（A,B）,然后向前移动的时候再次遇到（A,B）的时候采用标记符代替。

4.1 压缩

  当压缩数据的时候，前向缓冲区与移动窗口之间在做短语匹配的是后会存在2种情况:
  找不到匹配时：将未匹配的符号编码成符号标记（多数都是字符本身）
  找到匹配时：将其最长的匹配编码成短语标记。
  短语标记包含三部分信息：（滑动窗口中的偏移量（从匹配开始的地方计算）、匹配中的符号个数、匹配结束后的前向缓冲区中的第一个符号）。
  一旦把n个符号编码并生成响应的标记，就将这n个符号从滑动窗口的一端移出，并用前向缓冲区中同样数量的符号来代替它们，如此，滑动窗口中始终有最新的短语。通过图来进行解释：
  

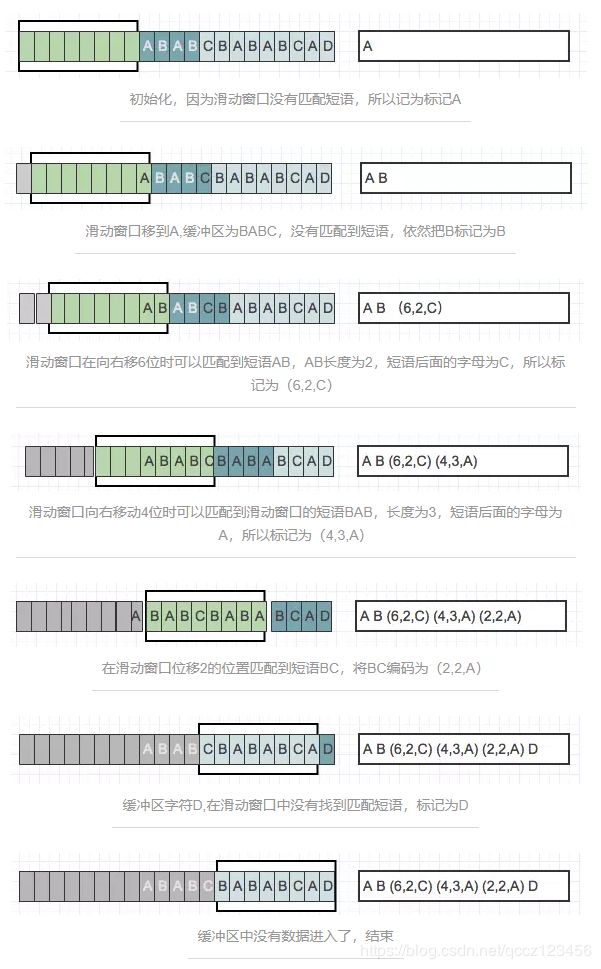
4.2 解压

  解压类似于压缩的逆向过程，通过解码标记和保持滑动窗口中的符号来更新解压数据。
  
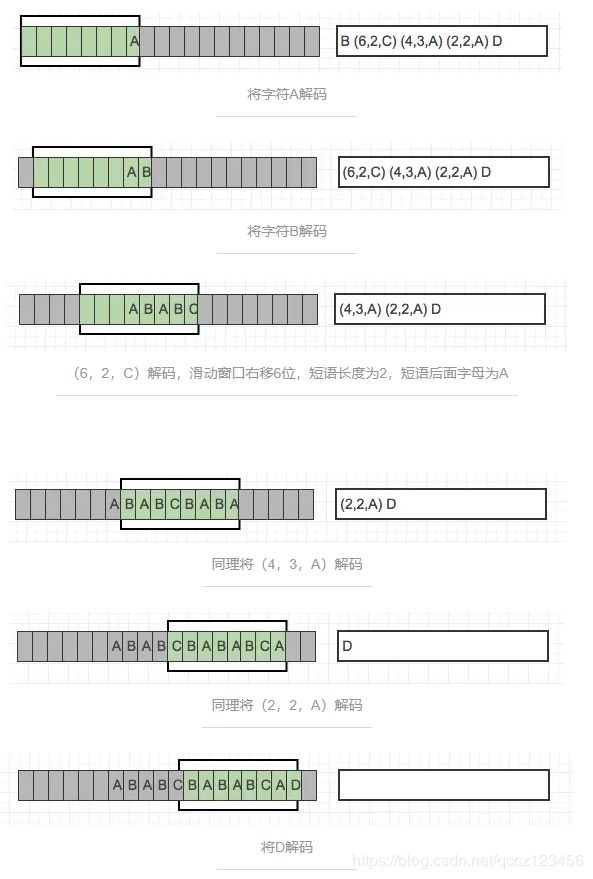
  解码字符标记：将标记编码成字符拷贝到滑动窗口中。
  解码短语标记：在滑动窗口中查找响应偏移量，同时找到指定长短的短语进行替换。
  但数组是无法直接用二进制来表示的，LZ77会把编码每八个数分成一组，每组前用一个前缀标示来说明这八个数的属性。比如数据流：A B A C A C B A C A按照LZ77的算法编码为：A B A C<2,2> <4,5>，刚好八个数。按照LZ77的规则，用“0”表示原文输出，“1”表示数组输出。所以这段编码就表示为：00001111B（等于0FH），因此得到完整的压缩编码表示：F A B A C 2 2 4 5。虽然表面上只缩短了1个字节的空间，但当数据流很长的时候就会突出它的优势，这种算法在zip格式中是经常用到。
  

（五）香农-范诺算法

  将序列分成两部分，使得左部频率总和尽可能接近右部频率总和。

（六）霍夫曼编码（Huffman Encoding）

  香农 - 法诺并不总是产生最优的前缀码：概率{0.35，0.17，0.17，0.16，0.15}是一个将分配非优化代码的Shannon-Fano的编码的一个例子。
  出于这个原因，香农 - 范诺几乎从不使用; 哈夫曼编码几乎是计算简单，生产总是达到预期最低的码字长度的制约下，每个符号是由一个整数组成一个代码代表的前缀码。在大多数情况下，[算术编码]可以产生比哈夫曼或的香农-范诺更大的整体压缩，因为它可以在小数位编码，这更接近实际的符号信息内容。然而，算术编码并没有取代像霍夫曼取代的香农-范诺一样取代哈夫曼，一方面是因为算术编码的计算成本的方式，因为它是由多个专利覆盖。
  
  例如：
  字符串：
    “beep boop beer!”

字符	次数
‘b’	3
‘e’	4
‘p’	2
‘ ’	2
‘o’	2
‘r’	1
‘!’	1

  然后，我把把这些东西放到Priority Queue中（用出现的次数据当 priority），我们可以看到，Priority Queue 是以Prioirry排序一个数组，如果Priority一样，会使用出现的次序排序。
  接下来把这个Priority Queue 转成二叉树。
  我们始终从queue的头取两个元素来构造一个二叉树（第一个元素是左结点，第二个是右结点），并把这两个元素的priority相加，并放回Priority中（再次注意，这里的Priority就是字符出现的次数）。
  然后，我们再把前两个取出来，形成一个Priority为2+2=4的结点，然后再放回Priority Queue中。继续我们的算法（我们可以看到，这是一种自底向上的建树的过程）。最终我们会得到下面这样一棵二叉树。
  此时，我们把这个树的左支编码为0，右支编码为1，这样我们就可以遍历这棵树得到字符的编码，比如：‘b’的编码是 00，’p’的编码是101， ‘r’的编码是1000。我们可以看到出现频率越多的会越在上层，编码也越短，出现频率越少的就越在下层，编码也越长。
  
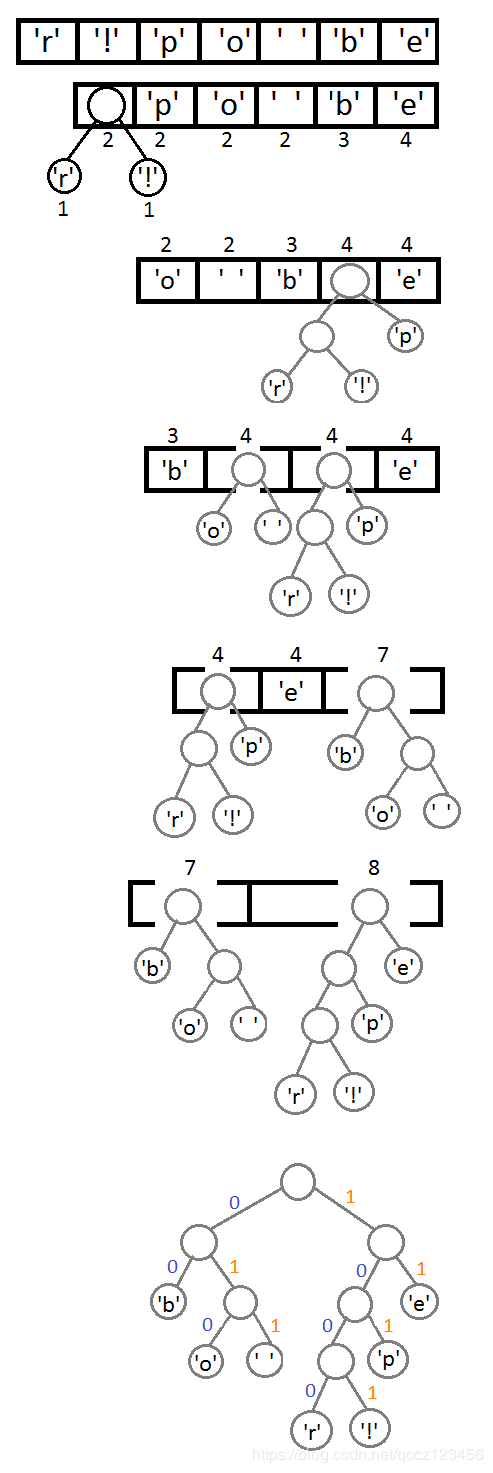
  最终我们可以得到下面这张编码表：

字符	霍夫曼编码
‘b’	00
‘e’	11
‘p’	101
‘ ’	011
‘o’	010
‘r’	1000
‘!’	1001

  这里需要注意一点，当我们encode的时候，我们是按“bit”来encode，decode也是通过bit来完成，比如，如果我们有这样的bitset “1011110111″ 那么其解码后就是 “pepe”。所以，我们需要通过这个二叉树建立我们Huffman编码和解码的字典表。
  这里需要注意的一点是，我们的Huffman对各个字符的编码是不会冲突的，也就是说，不会存在某一个编码是另一个编码的前缀，不然的话就会大问题了。因为encode后的编码是没有分隔符的。
  于是，对于我们的原始字符串 beep boop beer!
  其对就能的二进制为 : 0110 0010 0110 0101 0110 0101 0111 0000 0010 0000 0110 0010 0110 1111 0110 1111 0111 0000 0010 0000 0110 0010 0110 0101 0110 0101 0111 0010 0010 0001
  我们的Huffman的编码为： 0011 1110 1011 0001 0010 1010 1100 1111 1000 1001

（七）范式霍夫曼编码（Canonical Huffman Code）

7.1 为什么霍夫曼编码不好，而采用范式霍夫曼编码？
（1）解码器需要知道哈夫曼编码树的结构，因而编码器必须为解码器保存或传输哈夫曼编码树；
（2）
7.2 范式霍夫曼编码要求（1）是前缀编码（2）某一字符编码长度和使用二叉树建立的该字符的编码长度相同。
7.3 范式霍夫曼编码的步骤
（1）统计每个要编码符号的频率；
（2）依据这些频率信息求出，该符号在传统Huffman编码树中的深度，也就是该符号需要的位数、编码长度、码长；
（3）编码长度由短到长排列，按照以下方式计算范式霍夫曼编码的码：第一位码是按照霍夫曼编码树的码长全设为0，接下里的码是上一个编码+1；
（4）如果霍夫曼编码树的码长变长，则需要采用 本次编码 = 2*(本次码长-上次码长) * ( 上一个编码 + 1 )得到。
例如，依据上节的结果，建立范式霍夫曼编码：

字符	霍夫曼编码	霍夫曼编码码长	范式霍夫曼编码	备注
‘b’	00	2	00	按码长全设为0
‘e’	11	2	01	相同码长时，上一码+1
‘p’	101	3	100	不同码长时，2*(3-2)*（上一码 + 1）
‘ ’	011	3	101	相同码长时，上一码+1
‘o’	010	3	110	相同码长时，上一码+1
‘r’	1000	4	1110	不同码长时，2*(4-3) *（上一码 + 1）
‘!’	1001	4	1111	相同码长时，上一码+1

（八）算术编码

8.1 编码原理

（1）假设有一段数据需要编码，统计里面所有的字符和出现的次数。
（2）将区间 [0,1) 连续划分成多个子区间，每个子区间代表一个上述字符， 区间的大小正比于这个字符在文中出现的概率 p。概率越大，则区间越大。所有的子区间加起来正好是 [0,1)。
（3）编码从一个初始区间 [0,1) 开始，设置: low=0，high=1
（4）不断读入原始数据的字符，找到这个字符所在的区间，比如 [ L, H )，更新:
    low=low+(high−low)∗L
    high=low+(high−low)∗H
（5）最后将得到的区间 [low, high)中任意一个小数以二进制形式输出即得到编码的数据。

8.2 例程

  原始数据：ARBER
  计算出现的频率：

Symbol	Times	P
A	1	0.2
B	1	0.2
E	1	0.2
R	2	0.4

  将这几个字符的区间在 [0，1) 上按照概率大小连续一字排开，我们得到一个划分好的 [0，1)区间：

  开始编码，初始区间是 [0，1)。注意这里又用了区间这个词，不过这个区间不同于上面代表各个字符的概率区间 [0，1)。这里我们可以称之为编码区间，这个区间是会变化的，确切来说是不断变小。我们将编码过程用下图完整地表示出来：

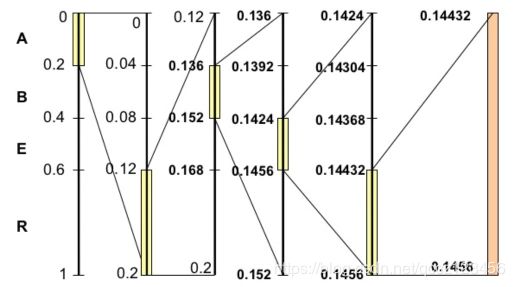
  拆解开来一步一步看：
  （1）刚开始编码区间是 [0，1)，即
    low=0
    high=1
  （2）第一个字符A的概率区间是 [0，0.2)，则 L = 0，H = 0.2，更新
    low=low+（high−low）∗L=0
    high=low+（high−low）∗H=0.2
  （3）第二个字符R的概率区间是 [0.6，1)，则 L = 0.6，H = 1，更新
    low=low+（high−low）∗L=0.12
    high=low+（high−low）∗H=0.2
  （4）第三个字符B的概率区间是 [0.2，0.4)，则 L = 0.2，H = 0.4，更新
    low=low+（high−low）∗L=0.136
    high=low+（high−low）∗H=0.152
  （5）如此以上往复计算。
  上面的图已经非常清楚地展现了算数编码的思想，我们可以看到一个不断变化的小数编码区间。每次编码一个字符，就在现有的编码区间上，按照概率比例取出这个字符对应的子区间。例如一开始A落在0到0.2上，因此编码区间缩小为 [0，0.2)，第二个字符是R，则在 [0，0.2)上按比例取出R对应的子区间 [0.12，0.2)，以此类推。每次得到的新的区间都能精确无误地确定当前字符，并且保留了之前所有字符的信息，因为新的编码区间永远是在之前的子区间。最后我们会得到一个长长的小数，这个小数即神奇地包含了所有的原始数据，不得不说这真是一种非常精彩的思想。

8.3 解码

  如果你理解了编码的原理，则解码的方法显而易见，就是编码过程的逆推。从编码得到的小数开始，不断地寻找小数落在了哪个概率区间，就能将原来的字符一个个地找出来。例如得到的小数是0.14432，则第一个字符显然是A，因为它落在了 [0，0.2)上，接下来再看0.14432落在了 [0，0.2)区间的哪一个相对子区间，发现是 [0.6，1)， 就能找到第二个字符是R，依此类推。在这里就不赘述解码的具体步骤了。
  编程实现:
  算数编码的原理简洁而又精致，理解起来也不很困难，但具体的编程实现其实并不是想象的那么容易，主要是因为小数的问题。虽然我们在讲解原理时非常容易地不断计算，但如果真的用编程实现，例如C++，并且不借助第三方数学库，我们不可能简单地用一个double类型去表示和计算这个小数，因为数据和编码可以任意长，小数也会到达小数点后成千上万位。
  怎么办？其实也很容易，小数点是可以挪动的。给定一个编码区间，例如从上面例子里最后的区间 [0.14432，0.1456)开始，假定还有新的数据进来要继续编码。现有区间小数点后的高位0.14其实是确定的，那么实际上14已经可以输出了，小数点可以向后移动两位，区间变成 [0.432，0.56)，在这个区间上继续计算后面的子区间。这样编码区间永远保持在一个有限的精度要求上。
  上述是基于十进制的，实际数字是用二进制表示的，当然原理是一样的，用十进制只是为了表述方便。算数编码／解码的编程实现其实还有很多tricky的东西和corner case，我当时写的时候debug了好久，因此我也建议读者自己动手写一遍，相信会有收获。

8.4 算术编码 vs 哈夫曼编码

  这其实是我想重点探讨的一个部分。在这里默认你已经懂哈夫曼编码，因为这是一种最基本的压缩编码，算法课都会讲。哈夫曼编码和算数编码都属于熵编码，仔细分析它们的原理，这两种编码是十分类似的，但也有微妙的不同之处，这也导致算数编码的压缩率通常比哈夫曼编码略高，这些我们都会加以探讨。
  不过我们首先要了解什么是熵编码，熵是借用了物理上的一个概念，简单来说表示的是物质的无序度，混乱度。信息学里的熵表示数据的无序度，熵越高，则包含的信息越多。其实这个概念还是很抽象，举个最简单的例子，假如一段文字全是字母A，则它的熵就是0，因为根本没有任何变化。如果有一半A一半B，则它可以包含的信息就多了，熵也就高。如果有90%的A和10%的B，则熵比刚才的一半A一半B要低，因为大多数字母都是A。
  熵编码就是根据数据中不同字符出现的概率，用不同长度的编码来表示不同字符。出现概率越高的字符，则用越短的编码表示；出现概率地的字符，可以用比较长的编码表示。这种思想在哈夫曼编码中其实已经很清晰地体现出来了。那么给定一段数据，用二进制表示，最少需要多少bit才能编码呢？或者说平均每个字符需要几个bit表示？其实这就是信息熵的概念，如果从数学上理论分析，香农天才地给出了如下公式：
  
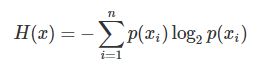
  其中 p (xi) 表示每个字符出现的概率。log对数计算的是每一个字符需要多少bit表示，对它们进行概率加权求和，可以理解为是求数学期望值，最后的结果即表示最少平均每个字符需要多少bit表示，即信息熵，它给出了编码率的极限。
  算术编码和哈夫曼编码的比较
  在这里我们不对信息熵和背后的理论做过多分析，只是为了帮助理解算数编码和哈夫曼编码的本质思想。为了比较这两种编码的异同点，我们首先回顾哈夫曼编码，例如给定一段数据，统计里面字符的出现次数，生成哈夫曼树，我们可以得到字符编码集：

Symbol	Times	Encoding
a	3	00
b	3	01
c	2	10
d	1	110
e	2	111

  仔细观察编码所表示的小数，从0.0到0.111，其实就是构成了算数编码中的各个概率区间，并且概率越大，所用的bit数越少，区间则反而越大。如果用哈夫曼编码一段数据abcde，则得到：00 01 10 110 111。
  如果点上小数点，把它也看成一个小数，其实和算数编码的形式很类似，不断地读入字符，找到它应该落在当前区间的哪一个子区间，整个编码过程形成一个不断收拢变小的区间。
  由此我们可以看到这两种编码，或者说熵编码的本质。概率越小的字符，用更多的bit去表示，这反映到概率区间上就是，概率小的字符所对应的区间也小，因此这个区间的上下边际值的差值越小，为了唯一确定当前这个区间，则需要更多的数字去表示它。我们仍以十进制来说明，例如大区间0.2到0.3，我们需要0.2来确定，一位足以表示；但如果是小的区间0.11112到0.11113，则需要0.11112才能确定这个区间，编码时就需要5位才能将这个字符确定。其实编码一个字符需要的bit数就等于 -log ( p )，这里是十进制，所以log应以10为底，在二进制下以2为底，也就是香农公式里的形式。
  哈夫曼编码的不同之处就在于，它所划分出来的子区间并不是严格按照概率的大小等比例划分的。例如上面的d和e，概率其实是不同的，但却得到了相同的子区间大小0.125；再例如c，和d，e构成的子树，c应该比d，e的区间之和要小，但实际上它们是一样的都是0.25。我们可以将哈夫曼编码和算术编码在这个例子里的概率区间做个对比：
  
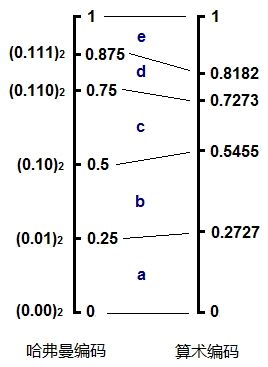
  这说明哈夫曼编码可以看作是对算数编码的一种近似，它并不是完美地呈现原始数据中字符的概率分布。也正是因为这一点微小的偏差，使得哈夫曼编码的压缩率通常比算数编码略低一些。或者说，算数编码能更逼近香农给出的理论熵值。
  更好地理解，最简单的例子
  比如有一段数据，A出现的概率是0.8，B出现的概率是0.2，现在要编码数据：
  AAA…AAABBB…BBB (800个A，200个B)
  如果用哈夫曼编码，显然A会被编成0，B会被编成1，如果表示在概率区间上，则A是 [0, 0.5)，B是 [0.5, 1)。为了编码800个A和200个B，哈夫曼会用到800个0，然后跟200个1：
  0.000…000111…111 (800个0，200个1)
  在编码800个A的过程中，如果我们试图去观察编码区间的变化，它是不断地以0.5进行指数递减，最后形成一个 [0, 0.5^800) 的编码区间，然后开始B的编码。
  但是如果是算术编码呢？因为A的概率是0.8，所以算数编码会使用区间 [0, 0.8) 来编码A，800个A则会形成一个区间 [0, 0.8^800)，显然这个区间比 [0, 0.5^800) 大得多，也就是说800个A，哈夫曼编码用了整整800个0，而算数编码只需要不到800个0，更少的bit数就能表示。
  当然对B而言，哈夫曼编码的区间大小是0.5，算数编码是0.2，算数编码会用到更多的bit数，但因为B的出现概率比A小得多，总体而言，算术编码”牺牲“B而“照顾”A，最终平均需要的bit数就会比哈夫曼编码少。而哈夫曼编码，由于其算法的特点，只能“不合理”地使用0.5和0.5的概率分布。这样的结果是，出现概率很高的A，和出现概率低的B使用了相同的编码长度1。两者相比，显然算术编码能更好地实现熵编码的思想。
  从另外一个角度来看，在哈夫曼编码下，整个bit流可以清晰地分割出原始字符串：
  
  而在算术编码下，每一个字符并不是严格地对应整数个bit的，有些字符与字符之间的边界可能是模糊的，或者说是重叠的，所以它的压缩率会略高：
  
  当然这样的解释并不完全严格，如果一定要究其原因，那必须从数学上进行证明，算数编码的区间分割是更接近于信息熵的结果的，这就不在本文的讨论范围了。在这里我只是试图用更直观地方式解释算数编码和哈夫曼编码之间微妙的区别，以及它们同属于熵编码的本质性原理。

8.5 总结

  算术编码的讲解就到这里。说实话我非常喜欢这种编码以及它所蕴含的思想，那种触及了数学本质的美感。如果说哈夫曼编码只是直观地基于概率，优化了字符编码长度实现压缩，那么算术编码是真正地从信息熵的本质，展现了信息究竟是以怎样的形式进行无损压缩，以及它的极限是什么。在讨论算术编码时，总是要提及哈夫曼编码，并与之进行比较，我们必须认识到它们之间的关系，才能对熵编码有一个完整的理解。
reference：
https://segmentfault.com/img/bVWFcv?w=515&h=287