李嘉璇 TensorFlow技术解析与实战 第四章笔记 TensorFlow基础知识

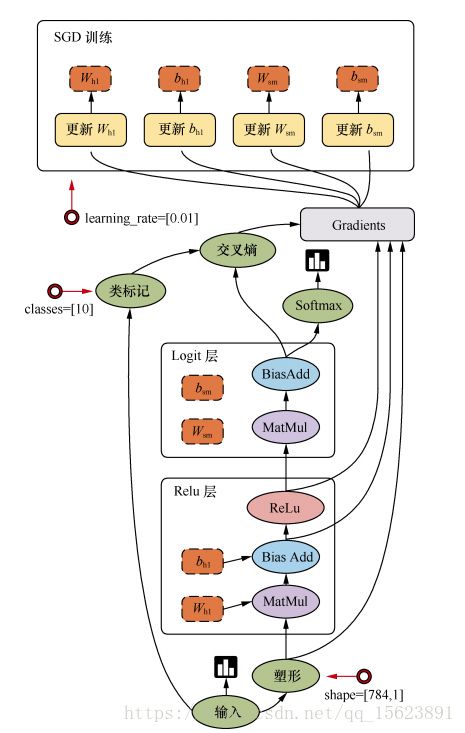
系统架构

• 最下层是网络通信层和设备管理层。网络通信层包括 gRPC（google Remote Procedure Call Protocol）和远程直接数据存取（Remote DirectMemory Access， RDMA），这都是在分布式计算时需要用到的。设备管理层包括 TensorFlow 分别在 CPU、 GPU、 FPGA 等设备上的实现，也就是对上层提供了一个统一的接口，使上层只需要处理卷积等逻辑，而不需要关心在硬件上的卷积的实现过程。
• 数据操作层，主要包括卷积函数、激活函数等操作。再往上是图计算层，也是我们要了解的核心，包含本地计算图和分布式计算图的实现。
  
• API 层和应用层。
  
  

编程模型

输入、塑性、RELU非线性激活、逻辑层、softmax输出、交叉熵、梯度、SGD训练。

TensorFlow支持的张量具有的数据属性

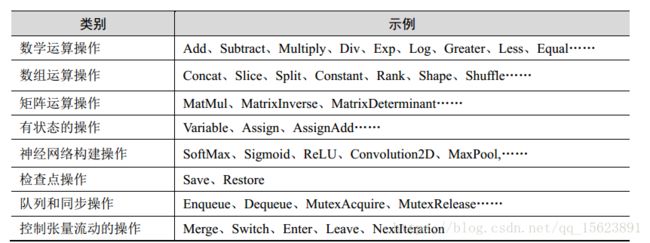
TensorFlow实现的算子

常用API

tf.Graph 类

tf.Operation 类

tf.Tensor 类

tf.Tensor 类是操作输出的符号句柄，它不包含操作输出的值，而是提供了一种在 tf.Session中计算这些值的方法。这样就可以在操作之间构建一个数据流连接，使 TensorFlow 能够执行一个表示大量多步计算的图形。

可视化

可视化时，需要在程序中给必要的节点添加摘要（summary），摘要会收集该节点的数据，并标记上第几步、时间戳等标识，写入事件文件（event file）中。 tf.summary.FileWriter 类用于在目录中创建事件文件，并且向文件中添加摘要和事件，用来在 TensorBoard 中展示。

变量作用域（没懂）

日后再补

batch normalization 批标准化

• ICS（Internal Covariate Shift）理论：源域和目标域的数据分布是一致的，即训练数据和测试数据是满足相同分布的。
• Covariate Shift 是指训练集的样本数据和目标样本集分布不一致时，训练得到的模型无法很好地泛化（generalization）。（源域与目标域的条件概率相同，但边缘概率不同）

方法

批标准化一般用在非线性映射（激活函数）之前，对 x=Wu+b 做规范化，使结果（输出信号各个维度）的均值为 0，方差为 1。让每一层的输入有一个稳定的分布会有利于网络的训练。 （理解为mean normalization？）

归一化均值为0，方差为1。规范化，这里也可以称为标准化，是将数据按比例缩放，使之落入一个小的特定区间。这里是指将数据减去平均值，再除以标准差。 

优点

• 神经网络收敛速度慢或梯度爆炸等无法训练的情况下，可以尝试。
• 加大学习速率。
• 更容易跳出局部最小值。
• 破坏原来的数据分布，一定程度上缓解过拟合问题。

（见Ng课程笔记

https://yoyoyohamapi.gitbooks.io/mit-ml/content/%E7%BA%BF%E6%80%A7%E5%9B%9E%E5%BD%92/articles/%E7%89%B9%E5%BE%81%E7%BC%A9%E6%94%BE.html

https://yoyoyohamapi.gitbooks.io/mit-ml/content/%E7%89%B9%E5%BE%81%E9%99%8D%E7%BB%B4/articles/PCA.html）

神经元函数及优化方法

激活函数

平滑非线性的激活函数，如 sigmoid、 tanh、 elu、 softplus 和 softsign，也包括连续但不是处处可微的函数 relu、 relu6、 crelu 和 relu_x，以及随机正则化函数 dropout：

• tf.nn.relu()
• tf.nn.sigmoid()
• tf.nn.tanh()
• tf.nn.elu()
• tf.nn.bias_add()
• tf.nn.crelu()
• tf.nn.relu6()
• tf.nn.softplus()
• tf.nn.softsign()
• tf.nn.dropout() # 防止过拟合，用来舍弃某些神经元

激活函数输入和输出的维度完全相同，常见的激活函数有sigmoid、tanh、relu、softplus四种。

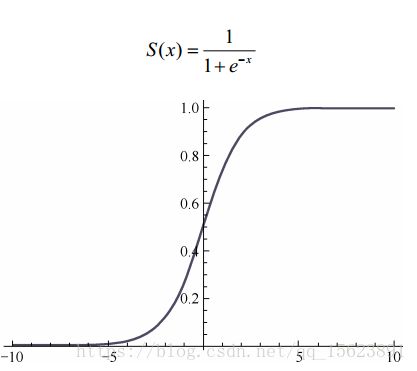
sigmoid函数：

sigmoid 函数的优点在于，它的输出映射在(0,1)内，单调连续，非常适合用作输出层，并且求导比较容易。但是，它也有缺点，因为软饱和性，一旦输入落入饱和区， f'(x)就会变得接近于 0，很容易产生梯度消失。

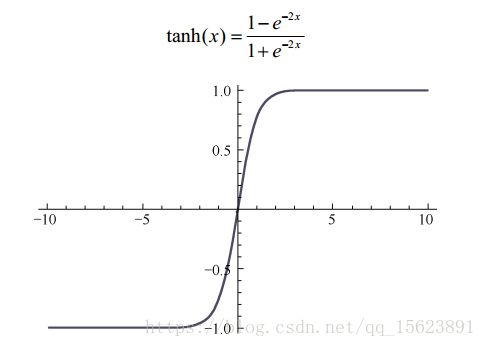
tanh函数：

tanh 函数也具有软饱和性。因为它的输出以 0 为中心，收敛速度比 sigmoid 要快。但是仍无法解决梯度消失的问题。

relu函数和softplus函数：

relu 函数是目前最受欢迎的激活函数。 softplus可以看作是 ReLU的平滑版本。 relu定义为 f(x)=max(x,0)。softplus 定义为 f(x)=log(1+exp(x))。

relu函数的缺点：relu函数在 x<0 时硬饱和。由于 x>0 时导数为 1，所以， relu 能够在 x>0 时保持梯度不衰减，从而缓解梯度消失问题，还能够更很地收敛，并提供了神经网络的稀疏表达能力。但是，随着训练的进行，部分输入会落到硬饱和区（x<0时，导数为0），导致对应的权重无法更新。

除了 relu 本身外， TensorFlow 还定义了 relu6，也就是定义在 min(max(features, 0), 6)的tf.nn.relu6(features, name=None)，以及 crelu，也就是 tf.nn.crelu(features, name=None)。

dropout函数：一个神经元将以概率 keep_prob 决定是否被抑制。如果被抑制，该神经元的输出就为 0；如果不被抑制，那么该神经元的输出值将被放大到原来的 1/keep_prob 倍。 

dropout 在论文中最早被提出时是这么做的：在训练的时候用概率 p 丢弃，然后在预测的时候，所有参数按比例缩小，也就是乘以 p。

不理解：在默认情况下，每个神经元是否被抑制是相互独立的。但是否被抑制也可以通过 noise_shape 来调节。当 noise_shape[i] == shape(x)[i]时， x 中的元素是相互独立的。如果 shape(x) = [k, l, m, n]，x 中的维度的顺序分别为批、行、列和通道，如果 noise_shape = [k, 1, 1, n]，那么每个批和通道都是相互独立的，但是每行和每列的数据都是关联的，也就是说，要不都为 0，要不都还是原来的值。 （noise__shape是怎么设定的？）

激活函数的选择：

当输入数据特征相差明显时，用 tanh 的效果会很好，且在循环过程中会不断扩大特征效果并显示出来。当特征相差不明显时， sigmoid 效果比较好。同时，用 sigmoid 和 tanh 作为激活函数时，需要对输入进行规范化，否则激活后的值全部都进入平坦区，隐层的输出会全部趋同，丧失原有的特征表达。而 relu 会好很多，有时可以不需要输入规范化来避免上述情况。因此，现在大部分的卷积神经网络都采用 relu 作为激活函数。大概有 85%～90%的神经网络会采用 ReLU， 10%～15%的神经网络会采用 tanh，尤其用在自然语言处理上。

卷积函数

池化函数

分类函数（输出函数）

TensorFlow 中常见的分类函数主要有 sigmoid_cross_entropy_with_logits、 softmax、 log_softmax、softmax_cross_entropy_with_logits 等。

tf.nn.sigmoid_cross_entropy_with_logits(logits, targets, name=None) tf.nn.softmax(logits, dim=-1, name=None) tf.nn.log_softmax(logits, dim=-1, name=None) tf.nn.softmax_cross_entropy_with_logits(logits, labels, dim=-1, name=None) tf.nn.sparse_softmax_cross_entropy_with_logits(logits, labels, name=None)

tf.nn.sigmoid_cross_entropy_with_logits

这个函数的输入要格外注意，如果采用此函数作为损失函数，在神经网络的最后一层不需要进行 sigmoid 运算。

tf.nn.softmax

tf.nn.softmax(logits, dim=-1, name=None)计算 Softmax 激活，也就是 softmax = exp(logits) /reduce_sum(exp(logits), dim)。

tf.nn.log_softmax

tf.nn.log_softmax(logits, dim=-1, name=None)计算 log softmax 激活，也就是 logsoftmax =logits - log(reduce_sum(exp(logits), dim))

tf.nn.softmax_cross_entropy_with_logits

tf.nn.softmax_cross_entropy_with_logits(_sentinel=None, labels=None, logits=None, dim=-1,name =None)

tf.nn.sparse_softmax_cross_entropy_with_logits(logits, labels, name=None)

优化函数

BGD、SGD、Momentum、Nesterov Momentum、Adagrad、 Adadelta、RMSprop、Adam.

收敛函数

BGD

优点：使用所有训练数据进行计算，能够保证收敛，不需要逐渐减少学习速率。 缺点：每一步更新都需要使用所有的训练数据，随着训练的进行，速度会越来越慢。

SGD

优点：训练数据很大的时候，能以较快的速度进行收敛。 缺点：需要手动调整学习率，容易收敛到局部最优，并且在某些情况下可能困在鞍点。

Momentum法

Momentum 是模拟物理学中动量的概念，更新时在一定程度上保留之前的更新方向，利用当前的批次再微调本次的更新参数，因此引入了一个新的变量 v（速度），作为前几次梯度的累加。因此， Momentum 能够更新学习率，在下降初期，前后梯度方向一致时，能够加速学习；在下降的中后期，在局部最小值的附近来回震荡时，能够抑制震荡，加很收敛。

Nesterov Momentum法

优化学习速率

Adagrad法

Adagrad 法能够自适应地为各个参数分配不同的学习率，能够控制每个维度的梯度方向。这种方法的优点是能够实现学习率的自动更改：如果本次更新时梯度大，学习率就衰减得很一些；如果这次更新时梯度小，学习率衰减得就慢一些。（学习速率与梯度大小成正比）

Adadelta法

Adagrad 法仍然存在一些问题：其学习率单调递减，在训练的后期学习率非常小，并且需要手动设置一个全局的初始学习率。Adadelta 法用一阶的方法，近似模拟二阶牛顿法，解决了这些问题。

RMSprop 法

RMSProp 法与 Momentum 法类似，通过引入一个衰减系数，使每一回合都衰减一定比例。在实践中，对循环神经网络（RNN）效果很好。

Adam 法

Adam 的名称来源于自适应矩估计（adaptive moment estimation）。 Adam 法根据损失函数针对每个参数的梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。

模型的存储与加载

TensorFlow 的 API 提供了以下两种方式来存储和加载模型。 （第一个只包含权重和其他在程序中定义的变量，第二个只包含图形结构，不包含权重） （1）生成检查点文件（checkpoint file），扩展名一般为.ckpt，通过在 tf.train.Saver 对象上调用 Saver.save()生成。它包含权重和其他在程序中定义的变量，不包含图结构。如果需要在另一个程序中使用，需要重新创建图形结构，并告诉 TensorFlow 如何处理这些权重。 （2）生成图协议文件（graph proto file），这是一个二进制文件，扩展名一般为.pb，用tf.train.write_graph()保存，只包含图形结构，不包含权重，然后使用 tf.import_graph_def()来加载图形。 具体见PDF94页。

队列和线程

TensorFlow 中主要有两种队列，即 FIFOQueue 和 RandomShuffleQueue。

FIFOQueue

FIFOQueue 创建一个先入先出队列。例如，我们在训练一些语音、文字样本时，使用循环神经网络的网络结构，希望读入的训练样本是有序的，就要FIFOQueue。

import tensorflow as tf

q=tf.FIFOQueue(3,"float")

init=q.enqueue_many(([0.1,0.2,0.3],))

x=q.dequeue()

y=x+1

q_inc=q.enqueue([y])

with tf.Session() as sess:

    sess.run(init)

    quelen=sess.run(q.size())

    for i in range(2):

        sess.run(q_inc)

    quelen=sess.run(q.size())

    for i in range(quelen):

        print(sess.run(q.dequeue()))

RandomShuffleQueue

RandomShuffleQueue 创建一个随机队列，在出队列时，是以随机的顺序产生元素的。例如，我们在训练一些图像样本时，使用 CNN 的网络结构，希望可以无序地读入训练样本，就要用RandomShuffleQueue，每次随机产生一个训练样本。

import tensorflow as tf

q=tf.RandomShuffleQueue(capacity=10,min_after_dequeue=2,dtypes="float")

sess=tf.Session()

for i in range(0,10):

    sess.run(q.enqueue(i))

for i in range(0,8):

    print(sess.run(q.dequeue()))

队列管理器

暂时用不到

线程和协调器

暂时用不到

加载数据

预加载数据

示例如下：

x1=tf.constant([2,3,4])

x2=tf.constant([4,0,1])

y=tf.add(x1,x2)

这种方式的缺点在于，将数据直接嵌在数据流图中，当训练数据较大时，很消耗内存。

填充数据

使用sess.run()的feed_dict参数，将python产生的数据填充给后端。 示例如下：

import tensorflow as tf

a1=tf.placeholder(tf.int16)

a2=tf.placeholder(tf.int16)

b=tf.add(a1,a2)

li1=[2,3,4]

li2=[4,0,1]

with tf.Session() as sess:

    print(sess.run(b,feed_dict={a1:li1,a2:li2}))

填充的方式也有数据量大、消耗内存等缺点，并且数据类型转换等中间环节增加了不小开销。

从文件读取数据

生成TFrecords文件 从队列中读取

用到时再看 PDF103页

实现一个自定义操作

PDF107页

本章主要讲解了 TensorFlow 的基础知识，包括系统架构、设计理念、基本概念，以及常用的 API、神经元函数和神经网络，还介绍了存储与加载模型的方法以及线程和队列的知识，最后介绍了自定义操作的方法。