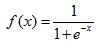基于神经网络的手写数字识别（上）
导读：
近期人工智能火热，十分好奇，决定了解一些基础知识。
本篇博客将从一个数学系渣渣本科生的角度，以学习记录的方式，整理关于BP神经网络的基础知识，以及实现一个简单的BP神经网络实现手写数字识别。
网络上关于 手写数字识别BP神经网络实现 的博客和教程很多，有些写的十分详细，质量很高，但是有些教程存在一些关键性问题，我在学习的时候被坑了不少。例如有些博客中对于神经网络训练的原理讲解十分详细，但事实上对于 具体的 手写数字识别 的训练过程并没有考虑多样本，多输出的情况应该如何调整相应算法，导致训练结果只适合于单张特例学习，或者某样本集的学习，不符合普遍的数字识别。或者考虑到了上述问题，但对原理缺乏介绍。本篇博客将针对这些问题给出详细的解释。
由于本人相关知识水平，文字水平有限，难免出现错误，有些可能是思路上的重大错误。望海涵。
开始进入正题吧。
机器学习基础中的基础：BP神经网络(下称BPnet)
计算机作为一种计算工具，想让其拥有学习功能，自动的学习某种简单的行为模式，看起来是不合实际的。但是，如果把机器学习看作是一种 函数的拟合过程 一切似乎又变得合理起来。为什么要这样说？
我们先看看生物的学习过程：
对于地球上的生物，学习可能就是完成某一条件反射的建立，例如听到下课铃，就想到吃午饭。
大脑是怎么运作的呢？主流的想法是，接受到声波之后，由听力系统产生的神经信号传播到大脑，引起特定区域的神经细胞活跃，这些活跃的神经细胞继续影响其他神经细胞，一系列的神经兴奋与抑制完成的对信号的处理，然后指导身体做出动作，完成条件反射。
模拟这个过程：
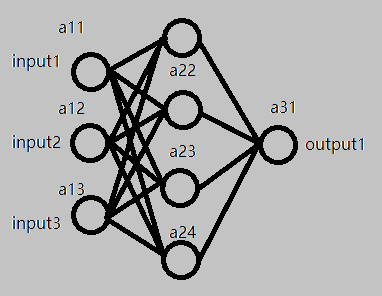
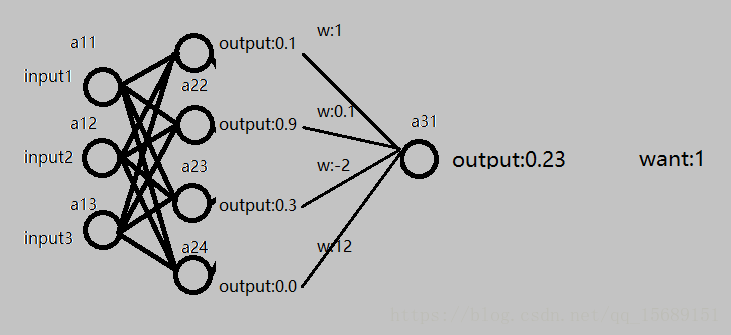
图1-1
(图中的每一个小圆点都是一个神经节点。)
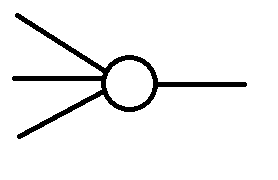
每一个小圆点的工作模式是这样的：
左侧的若干条线段代表若干个输入，右侧的线段代表输出。对应多个输入，小圆点会给出唯一的输出。这不就是一个多元函数吗？
事实上，我们假设每一个小圆点都是这样的一个函数：
其中k为小圆点的编号，aij为小圆点的输入，wj实系数（权重），bk为一个常数。
我们希望，对于来自于其他神经节点的不同刺激，该神经节点应该受到不同影响，当影响高于某一个值时，该节点被激活，产生相应的输出。wj就表示了对于其他节点，该节点所受影响的大小，而bk为一个阈值，当所有刺激高于阈值的时候，该节点被激活。
举个例子：
假设一个节点有三个输入，对应的系数分别为 1，-2，3，该节点的阈值为-5
对于输入(1,2,3),利用上述公式，得到输出为1*1+2*-2+3*3-5=1
对于输入(1,1,1),得到的输出为1*1+1*-2+1*3-5=-3
也就是说，对于第一个输入，该节点被激活(输出为正)，并输出的激活的程度 1，对于第二个输入，该节点没有被激活(输出为负)，并且抑制程度为-3。
到这里我们就基本模拟了一个生物的神经细胞的工作模式。然而，可以明显看到存在问题：当一个节点被抑制的时候，它应该对后续的节点产生尽可能小的影响，然而我们的输出，尽管通过区分正负，判别的激活或者抑制的状态，却无法阻止一个抑制状态的节点对后续节点产生较大的影响。
有没有什么办法让输出值满足预期呢？即：一个节点在激活状态下输出它的兴奋程度，而在抑制状态下输出接的兴奋程度接近于0。
有：将输入结果放入代入函数：
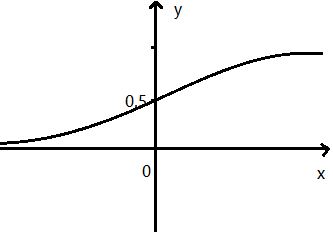
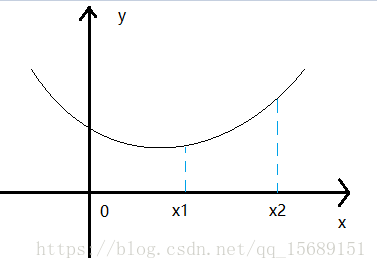
这个函数的图像为：
也就是当x大于0时，随x的增大而趋于1，当x小于0时，随x的减小而趋于0 。
这样就满足的我们的预期。
相应的，神经节点计算函数修改为：
函数就是上述的。
图1-1中的每一个小圆点都通过上述的方式组织起来，那么对于图中的一组输入，经过每个小圆点的计算，得到了最终的一个结果。这就是BPnet的基本模型。
通过调整每一个节点的权重w，阈值b，我们就可以改变这个神经网络的输出结果。事实上，不断地调整w与b的值，使BPnet的输出不断接近预期结果，就是训练BPnet，或者说机器学习的过程。
训练BPnet/反向传导/梯度下降法
在实际应用中，BPnet基本上不会如图1-1那样简单，往往一个BPnet将会有多个中间层，多达几十几百个输入，几十几百个最终输出。拿 手写数字识别 为例，如果读取一张15*15像素大小的图片，将这255个像素点的灰度值作为输入，进入含有一层中间层，中间节点为50，产生对应0~9的十个输出节点的BPnet，将会有255*50+50*10=13250个权重w，50+10=60个阈值b需要我们调整，以使得最终的输出满足预期，显然人工调整是一项不可能完成的任务。我们需要一些数学方法来让计算机完成调整过程。
先看看预期：
图1-2
对于之前的模型，假设有如图1-2的情形：期望的输出是1，BPnet给出的输出为0.23，中间层的输出以及权重在图上分别标出。
显然，此时希望最终的输出值变大，有三种方式可以走：
1.调整阈值：例如直接改变最终输出的阈值b，使b=b+0.77 这样就直接使得输出结果为1 满足预期。或者改变中间层的阈值，也可以间接的改变输出结果。
2.改变权重w：例如将图中中间层到最后一层的全体权重变大，因为中间层的输出结果都非负，也可使最终输出变大，接近预期。
3.改变中间层的输入：例如，如果将图中第一次的输出结果，即中间层的输入值修改，使得中间层的输出改变，也可以影响最终输出，但实际上我们不可以直接对中间层的输入进行修改，因为这些输入是由上一次计算得出的。但是我们可以得到对于输入值修改的预期：例如，因为中间层的第1，2，4号节点对应的最后一层权重都是正数，如果使得这些值变大，那么就可以使得输出结果更接近预期。想让这些节点输出变大，如果比如让a21节点的输出变大，因为已知a21的计算公式为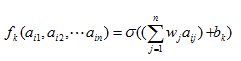，那么如果让正权重wj对应的a1i变大，就可以实现预期。而让a1i变大，可以重复方式1，2即调整a1i的阈值或者权重来完成。
通过计算结果，利用方式1，2，3不断地向前一层，前前一层做出修改，这个过程就是反向传导。
之前已经解释过，人工完成调整计算量巨大，不可能完成。于是引入梯度下降法。
学过数学分析的同学都知道，对于多元函数，梯度是函数增长最快的方向，那么负梯度就是函数下降最快的方向。
梯度：各分量为 函数对各变量分别求偏导再乘单位方向向量 的一个向量。
对于一个BPnet，记输出为Oi，预期输出为Ci
输出与预期输出的方差为：
那么让S不断减小的过程就是让输出接近预期输出的过程。
因为Oi是关于全部权重w，全部阈值b，全部中间输出的函数，那么S也是关于全部权重w，全部阈值b，全部中间输出的函数，求得S的负梯度，就可以知道w，b，以及中间输出 应该怎样调整。
举个例子：
对于一元函数
，一阶导数就是它的梯度，我们希望通过改变x的值似的y尽量小。
如图：
回头看BPnet，模仿上述过程，不断的求梯度，再让权重或者阈值修改一点点，我们会不断接近预期。
下面给出计算：
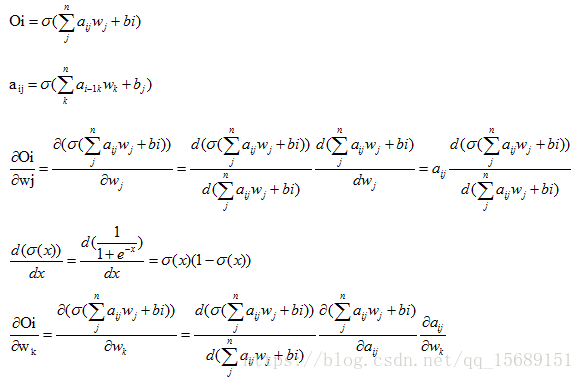
对于每一次输入，利用上述方法，对权重做出一点点修改，重复多次之后，BPnet将被训练为一个较好的拟合。
至此，我们以及明白了何为BPnet，以及BPnet的训练方法，核心为梯度法和反向传到过程。我们现在就可以做对于特定的某一组输入，固定的某一组输出的BPnet的训练了。然而距离我们的目标：实现多输入源，多输出结果 即实现手写数字识别 还有一定距离，毕竟现在的模型太过简单，考虑的因素太少。
下期继续。
感谢您认真地看到了这里。