论文阅读笔记
论文名称:
Unsupervised Learning of Monocular Depth Estimation and Visual Odometry with Deep Feature Reconstruction
文章目录
- 1 摘要
- 2 引言
- 3 方法
- 3.1 Image reconstruction as supervision(图像重建作为监督)
- 3.2 Differentiable geometry modules
- 3.3 Feature reconstruction as supervision(利用特征重建作为监督信息)
- 3.4 训练损失
1 摘要
尽管基于学习的方法在单视图深度估计和视觉测距中显示出有希望的结果,但是大多数现有方法以受监督的方式处理任务。最近的单视图深度估计方法通过最小化光度误差来探索在没有完全监督的情况下学习的可能性。在本文中,我们探讨了立体照片序列在学习深度和视觉测距中的应用。立体照片序列的使用使得系统能够使用空间(在左右对之间)和时间(向前向后)光度扭曲误差,并且将场景深度和相机运动约束在共同的真实世界范围内。在测试时,我们的框架能够从单眼序列估计单视图深度和双视图测距。我们还展示了如何通过考虑深度特征的扭曲来改进标准光度翘曲损失。我们通过大量实验证明:
(i)单视深度和视觉测距的联合训练改善了深度预测,因为对深度施加了额外的约束并且实现了视觉测距的竞争结果;
(ii)基于特征的深度翘曲损失改善了单视图深度估计和视觉测距的简单光度翘曲损失。我们的方法在两个任务中都优于KITTI驾驶数据集的现有基于学习的方法。
2 引言
从单个图像理解场景的3D结构是机器感知中的基本问题。 从图像序列推断自我运动的相关问题同样是机器人技术中的基本问题,称为视觉测距估计(VO)。 这两个问题在机器人视觉研究中至关重要,因为基于图像的深度和测距的准确估计具有许多重要的应用,尤其是对于自动驾驶车辆。
虽然这两个问题一直是机器视觉研究的主题,因为该学科的起源,提出了许多几何解决方案,近来许多作品都将深度估计和视觉测距作为监督学习问题[1] [5] [ 21] [22]。这些方法尝试使用已经从具有地面实况数据的大型数据集训练的模型来预测深度或测距。然而,这些注释的获得是昂贵的,例如,昂贵的激光或深度相机来收集深度。 Garg等人最近的一篇着作[6]认识到这些任务适用于无监督框架,其中作者建议使用光度扭曲误差作为自监督信号来训练卷积神经网络(ConvNet / CNN)用于单视图深度估计。 [6]方法如[9] [19] [41]使用基于光度误差的监督来学习与完全监督方法相当的深度估计。具体来说,[6]和[9]使用立体对中左右图像之间的光度扭曲误差来学习深度。认识到这一概念的普遍性,[44]使用单眼序列联合训练两个神经网络进行深度和测距估计。然而,依赖于两帧视觉里程计算估计框架,[44]遭受每帧尺度模糊问题,因为缺少相机平移的实际度量缩放并且仅知道方向。对每帧的平移规模进行良好估计对于任何同时定位和映射(SLAM)系统的成功至关重要。大多数单眼SLAM框架中的精确相机跟踪依赖于保持地图在多个图像上的尺度一致性,这是使用单个比例尺图执行的。在没有用于跟踪的全局地图的情况下,对于每帧尺度参数的昂贵的束调整或者来自已经检测到的地平面的恒定相机高度的附加假设对于精确跟踪变得必不可少[34]。
在这项工作中,我们提出了一个框架,它使用立体视频序列(如图1所示)共同学习单个视图深度估计器和单眼测距估计器并进行训练。 我们的方法可以被理解为用于深度估计的无监督学习和用于在立体对之间已知的姿势的半监督。 立体图像序列的使用使得能够使用空间(左右对之间)和时间(前向 - 后向)光度扭曲误差,并且将场景深度和相机运动限制在共同的真实世界范围内(由 立体声基线)。 然后,使用单个相机用于纯帧到帧VO估计而无需任何映射,可以推断(即深度和里程计估计)而没有任何尺度模糊。
此外,虽然之前的工作已经显示出使用光度扭曲误差作为自我监视信号的功效,但是图像强度或颜色的简单扭曲带有关于亮度/颜色一致性的自身假设,并且还必须伴随着正则化以产生“ 当光度信息不明确时,例如在均匀着色的区域(见第3.3节),合理的“扭曲”。 我们提出了额外的深度特征重建损失,其考虑了上下文信息而不是单独的每像素颜色匹配。
总之,我们做出以下贡献:
(i)一个无监督的框架,用于联合学习深度估计器和视觉里程计算器,不会受到尺度模糊的影响;
(ii)利用空间和时间图像对可用的全部约束来改进现有技术的单视图深度估计;
(iii)产生最先进的帧到帧测距结果,显着提高[44]并与几何方法相提并论;
(iv)除了基于颜色强度的图像重建损失之外还使用新颖的特征重建损失,其显着地改善了深度和测距估计精度。
3 方法
本节描述了我们的框架(如图2所示),用于从立体图像序列中联合学习单个视图深度ConvNet( C N N D CNN_D CNND)和视觉测距ConvNet( C N N V O CNN_{VO} CNNVO)。 立体序列学习框架克服了单眼序列的缩放模糊问题,并使系统能够利用左右(空间)和前后(时间)一致性检查。

3.1 Image reconstruction as supervision(图像重建作为监督)
我们框架中的基本监督信号来自图像重建的任务。 对于两个附近的视图,我们能够从实时视图重建参考视图,假设参考视图的深度和两个视图之间的相对相机姿势是已知的。 由于可以通过ConvNet估计深度和相对相机姿势,因此真实视图和重建视图之间的不一致性允许ConvNet的训练。 然而,没有额外约束的单眼框架[44]会受到缩放模糊问题的困扰。 因此,我们提出了一种立体框架,该框架在给定由已知立体基线设置的额外约束的情况下将场景深度和相对相机运动约束在共同的真实世界范围内。
在我们提出的使用立体序列的框架中,对于每个训练实例,我们有一个时间对( I L , t 1 I_{L,t_1} IL,t1和 I L , t 2 I_{L,t_2} IL,t2)和一个立体对( I L , t 2 I_{L,t_2} IL,t2和 I R , t 2 I_{R,t_2} IR,t2),其中 I L , t 2 I_{L,t_2} IL,t2是参考视图,而 I L , t 1 I_{L,t_1} IL,t1和 I R , t 2 I_{R,t_2} IR,t2是实时视图。 我们可以合成两个参考视图, I L , t 1 ′ I'_{L,t_1} IL,t1′和 I R , t 2 ′ I'_{R,t_2} IR,t2′来自 I L , t 1 I_{L,t_1} IL,t1和 I R , t 2 I_{R,t_2} IR,t2。 合成过程可以表示为:
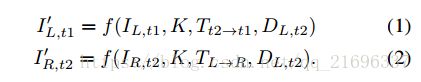
(在这里,论文采用了这样一种思路:将双目图像的左右图像分别取出,按左右视图和时间序列视图进行标记;对某一张参考图像来说,我们要为它生成两张重建视图(利用和他相邻的两张实施视图),分别恢复它的深度特征和相邻帧之间的相对位姿信息,恢复之后的结果用来作为网络的监督信息。)
其中f()是在3.2中定义的合成函数; D L , t 2 D_{L,t_2} DL,t2表示参考视图的深度图; T L − R T_{L-R} TL−R和 T t 2 − t 1 T_{t2-t1} Tt2−t1表示引用视图和实时视图之间的相关相机的位姿变换;K表示已知的相机内参。 D L , t 2 D_{L,t_2} DL,t2是视图 I L , t 2 I_{L,t_2} IL,t2通过 C N N D CNN_D CNND生成, T t 2 − t 1 T_{t2-t1} Tt2−t1是视图{ I L , t 1 I_{L,t_1} IL,t1, I L , t 2 I_{L,t_2} IL,t2}通过 C N N V O CNN_{VO} CNNVO生成。
合成视图和真实视图之间的图像重建损失被计算为用于训练 C N N D CNN_D CNND和 C N N V O CNN_{VO} CNNVO的监督信号。图像构造损失由以下表示: 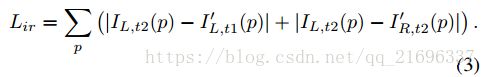
使用立体序列代替单眼序列的效果是双重的。立体对之间的已知相对姿势 T L − R T_L-R TL−R约束 C N N D CNN_D CNND和 C N N V O CNN_{VO} CNNVO以估计现实世界范围内的时间对之间的深度和相对姿势。 因此,我们的模型能够在测试时没有缩放模糊问题的情况下估计单个视图深度和双视图测距。 其次,除了仅具有一个实时视图的立体对之外,时间对还为参考视图提供第二实时视图。 多视图场景利用了立体和时间图像对可用的全部约束。
在本节中,我们描述了一个无监督的框架,它可以学习深度估计和视觉测距,而不会使用立体视频序列缩放模糊度问题.
3.2 Differentiable geometry modules
如公式1-2所示,我们学习框架中的一个重要功能是合成函数f()。 该功能包括两个可微分的操作,允许梯度传播用于ConvNet的训练。 这两个操作是极线几何变换和扭曲。 前者定义两个视图中的像素之间的对应关系,而后者通过扭曲实时视图来合成图像。
令 p L , t 2 p_{L,t_2} pL,t2为参考视图中像素的齐次坐标。 我们可以使用极线几何获得 p L , t 2 p_{L, t_2} pL,t2的投影坐标到实时视图,类似于[10,44]。 投影坐标是通过
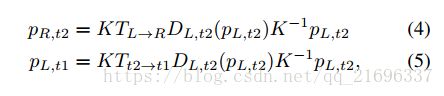
在从等式4-5获得投影坐标之后,可以使用[14]中提出的可微双线性插值机制(扭曲)从实时帧合成新的参考帧。
3.3 Feature reconstruction as supervision(利用特征重建作为监督信息)
我们上面提出的立体框架隐含地假设场景是朗伯(Lambertian),因此无论观察者的视角如何,亮度都是恒定的。 这种情况意味着图像重建损失对于训练ConvNets是有意义的。 任何违反该假设的行为都可能通过将错误的梯度传播回ConvNets来破坏训练过程。 为了提高我们框架的稳健性,我们提出了一个特征重建损失:我们不再单独使用3通道颜色强度信息(图像重建损失),而是探索使用密集特征作为附加监督信号。
3.4 训练损失
如第3.1节和第3.3节所述,我们框架中的主要监督信号来自图像重建损失,而特征重建损失则作为辅助监督。 此外,类似于[6] [44] [9],我们有深度平滑度损失,这促使预测的深度平滑。
为了获得平滑的深度预测,遵循[12] [9]采用的方法,我们通过引入边缘感知平滑项来鼓励深度在本地平滑。 如果在同一区域中显示图像连续性,则深度不连续性受到惩罚。 否则,对于已中断的深度,惩罚很小。 边缘感知平滑度损失表示为
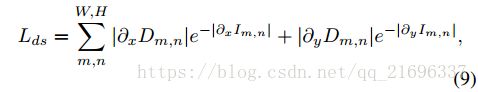
其中@x(:)和@y(:)分别是水平和垂直方向的偏导数。 注意 D m , n D_{m, n} Dm,n是上述正则化中的反向深度。
最终的损失函数为:
![]()