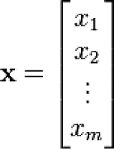多元线性回归推导过程
常用算法一 多元线性回归详解1
此次我们来学习人工智能的第一个算法:多元线性回归.文章会包含必要的数学知识回顾,大部分比较简单,数学功底好的朋友只需要浏览标题,简单了解需要哪些数学知识即可.
本章主要包括以下内容
数学基础知识回顾
什么是多元线性回归
多元线性回归的推导过程详解
如何求得最优解详解
数学基础知识回顾
1-截距
我们知道,y=ax+b这个一元一次函数的图像是一条直线.当x=0时,y=b,所以直线经过点(0,b),我们把当x=0时直线与y轴交点到x轴的距离称为直线y=ax+b图像在x轴上的截距,其实截距就是这个常数b.(有点拗口,多读两遍)
截距在数学中的定义是:直线的截距分为横截距和纵截距,横截距是直线与X轴交点的横坐标,纵截距是直线与Y轴交点的纵坐标。根据上边的例子可以看出,我们一般讨论的截距默认指纵截距.
2-斜率
既然已知y=ax+b中b是截距,为了不考虑常数b的影响,我们让b=0,则函数变为y=ax.
注意变换后表达式的图像.当a=1时,y=ax的图像是经过原点,与x轴呈45°夹角的直线(第一,三象限的角平分线),当a的值发生变化时,y=ax的图像与x轴和y轴的夹角也都会相应变化,我们称为这条直线y=ax的倾斜程度在发生变化,又因为a是决定直线倾斜程度的唯一的量(即便b不等于0也不影响倾斜程度),那么我们就称a为直线y=ax+b的斜率.
斜率在数学中的解释是 表示一条直线(或曲线的切线)关于(横)坐标轴倾斜程度的量.
3-导数
还是y=ax+b,我们知道这个函数的图像是一条直线,每个不同的x对应着直线上一点y.那么当自变量x的值变化的时候,y值也会随之变化.数学中我们把x的变化量成为Δx,把对应的y的变化量成为Δy,自变量的变化量Δx与因变量的变化量Δy的比值称为导数.记作y'.
y'=Δy/Δx
常用的求导公式在这部分不涉及,我们用到一个记住一个即可.
4-矩阵和向量
什么是向量:
向量就是一个数组.比如[1,2,3]是一个有三个元素的向量.
有行向量和列向量之分,行向量就是数字横向排列:X=[1,2,3],列向量是数字竖向排列,如下图
什么是矩阵:
矩阵就是元素是数组的数组,也就是多维数组,比如[[1,2,3],[4,5,6]]是一个两行三列的矩阵,也叫2*3的矩阵. 行代表内层数组的个数,列代表内层数组的元素数.一个矩阵中的所有数组元素相同.
5-向量的运算:
一个数乘以一个向量等于这个数同向量中的每个元素相乘,结果还是一个向量.
2 * [1,2,3] = [2,4,6]
一个行向量乘以一个列向量,是两个向量对位相乘再相加,结果是一个实数.
- = 11 + 22 + 3*3 = 14
附加:转置
转置用数学符号T来表示,比如W向量的转置表示为.转置就是将向量或者矩阵旋转九十度.一个行向量的转置是列向量,列向量的转置是行向量.一个m*n的矩阵转置是n*m的矩阵.
注:以上概念完全是为了读者能容易理解,并不严谨,若想知道上述名词的严谨解释,请自行百度.
什么是多元线性回归
我们知道y=ax+b是一元一次方程,y=ax1+bx2+c(1和2是角标,原谅我的懒)是二元一次方程.其中,"次"指的是未知数的最大幂数,"元"指的是表达式中未知数的个数(这里就是x的个数).那么"多元"的意思可想而知,就是表达式中x(或者叫自变量,也叫属性)有很多个.
当b=0时,我们说y=ax,y和x的大小始终符合y/x=a,图像上任意一点的坐标,y值都是x值的a倍.我们把这种横纵坐标始终呈固定倍数的关系叫做"线性".线性函数的图像是一条直线.所以我们知道了多元线性回归函数的图像一定也是一条直线.
现在我们知道了多元线性回归的多元和线性,而回归的概念我们在人工智能开篇(很简短,请点搜索"回归"查看概念)中有讲述,所以多元线性回归就是:用多个x(变量或属性)与结果y的关系式 来描述一些散列点之间的共同特性.
这些x和一个y关系的图像并不完全满足任意两点之间的关系(两点一线),但这条直线是综合所有的点,最适合描述他们共同特性的,因为他到所有点的距离之和最小也就是总体误差最小.
所以多元线性回归的表达式可以写成:
y= w0x0 + w1x1 + w2x2 + ... + wnxn (0到n都是下标哦)
我们知道y=ax+b这个线性函数中,b表示截距.我们又不能确定多元线性回归函数中预测出的回归函数图像经过原点,所以在多元线性回归函数中,需要保留一项常数为截距.所以我们规定 y= w0x0 + w1x1 + w2x2 + ... + wnxn中,x0=1,这样多元线性回归函数就变成了: y= w0 + w1x1 + w2x2 + ... + wnxn,w0项为截距.
如果没有w0项,我们 y= w0x0 + w1x1 + w2x2 + ... + wnxn就是一个由n+1个自变量所构成的图像经过原点的直线函数.那么就会导致我们一直在用一条经过原点的直线来概括描述一些散列点的分布规律.这样显然增大了局限性,造成的结果就是预测出的结果函数准确率大幅度下降.
有的朋友还会纠结为什么是x0=1而不是x2,其实不管是哪个自变量等于1,我们的目的是让函数 y= w0x0 + w1x1 + w2x2 + ... + wnxn编程一个包含常数项的线性函数.选取任何一个x都可以.选x0是因为他位置刚好且容易理解.
多元线性回归的推导过程详解
1-向量表达形式
我们前边回顾了向量的概念,向量就是一个数组,就是一堆数.那么表达式y= w0x0 + w1x1 + w2x2 + ... + wnxn是否可以写成两个向量相乘的形式呢?让我们来尝试一下.
假设向量W= [w1,w2...wn]是行向量,向量X= [x1,x2...xn],行向量和列向量相乘的法则是对位相乘再相加, 结果是一个实数.符合我们的逾期结果等于y,所以可以将表达式写成y=W * X.
但是设定两个向量一个是行向量一个是列向量又容易混淆,所以我们不如规定W和X都为列向量.所以表达式可以写成 (还是行向量)与向量X相乘.所以最终的表达式为:
y= * X,其中 也经常用 θ(theta的转置,t是上标)表示.
此处,如果将两个表达式都设为行向量,y=W * 也是一样的,只是大家为了统一表达形式,选择第一种形式而已.
2-最大似然估计
最大似然估计的意思就是最大可能性估计,其内容为:如果两件事A,B相互独立,那么A和B同时发生的概率满足公式
P(A , B) = P(A) * P(B)
P(x)表示事件x发生的概率.
如何来理解独立呢?两件事独立是说这两件事不想关,比如我们随机抽取两个人A和B,这两个人有一个共同特性就是在同一个公司,那么抽取这两个人A和B的件事就不独立,如果A和B没有任何关系,那么这两件事就是独立的.
我们使用多元线性回归的目的是总结一些不想关元素的规律,比如以前提到的散列点的表达式,这些点是随机的,所以我们认为这些点没有相关性,也就是独立的.总结不相关事件发生的规律也可以认为是总结所有事件同时发生的概率,所有事情发生的概率越大,那么我们预测到的规律就越准确.
这里重复下以前我们提到的观点.回归的意思是用一条直线来概括所有点的分布规律,并不是来描述所有点的函数,因为不可能存在一条直线连接所有的散列点.所以我们计算出的值是有误差的,或者说我们回归出的这条直线是有误差的.我们回归出的这条线的目的是用来预测下一个点的位置.
考虑一下,一件事情我们规律总结的不准,原因是什么?是不是因为我们观察的不够细或者说观察的维度不够多呢?当我们掷一个骰子,我们清楚的知道他掷出的高度,落地的角度,反弹的力度等等信息,那上帝视角的我们是一定可以知道他每次得到的点数的.我们观测不到所有的信息,所以我们认为每次投骰子得到的点数是不确定的,是符合一定概率的,未观测到的信息我们称为误差.
一个事件已经观察到的维度发生的概率越大,那么对应的未观测到的维度发生的概率就会越小.可以说我们总结的规律就越准确.根据最大似然估计
P(y) = P(x1,x2 ... xn)= P(x1) * P(x2) ... P(xn)
当所有事情发生的概率为最大时,我们认为总结出的函数最符合这些事件的实际规律.所以我们把总结这些点的分布规律问题转变为了 求得P(x1,x2 ... xn)= P(x1) * P(x2) ... P(xn)的发生概率最大.
3-概率密度函数
数学中并没有一种方法来直接求得什么情况下几个事件同时发生的概率最大.所以引用概率密度函数.
首先引入一点概念:
一个随机变量发生的概率符合高斯分布(也叫正太分布).此处为单纯的数学概念,记住即可.
高斯分布的概率密度函数还是高斯分布.公式如下:
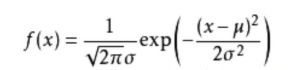
公式中x为实际值,u为预测值.在多元线性回归中,x就是实际的y,u就是θ * X.
既然说我们要总结的事件是相互独立的,那么这里的每个事件肯定都是一个随机事件,也叫随机变量.所以我们要归纳的每个事件的发生概率都符合高斯分布.
什么是概率密度函数呢?它指的就是一个事件发生的概率有多大,当事件x带入上面公式得到的值越大,证明其发生的概率也越大.需要注意,得到的并不是事件x发生的概率,而只是知道公式的值同发生的概率呈正比而已.
如果将y= θT* X中的每个x带入这个公式,得到如下函数
求得所有的时间发生概率最大就是求得所有的事件概率密度函数结果的乘积最大,则得到:
求得最大时W的值,则总结出了所有事件符合的规律.求解过程如下(这里记住,我们求得的是什么情况下函数的值最大,并不是求得函数的解):
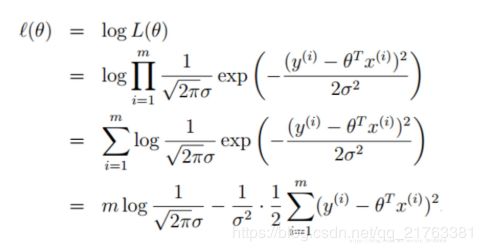
公式中,m为样本的个数,π和σ为常数,不影响表达式的大小.所以去掉所有的常数项得到公式:
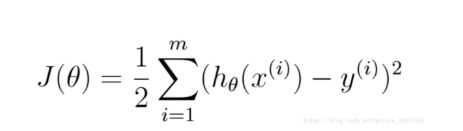
因为得到的公式是一个常数减去这个公式,所以求得概率密度函数的最大值就是求得这个公式的最小值.这个公式是一个数的平方,在我国数学资料中把他叫做最小二乘公式.所以多元线性回归的本质就是最小二乘.
本文转载自 https://blog.csdn.net/weixin_39445556/article/details/81416133