LeetCode--Majority Element--Boyer-Moore算法总结
找数组中的Majority Element,Majority Element的定义见下,对应着LeetCode上的两道题,直接看题:
LeetCode--169. Majority Element
给定一个长度为n的数组,找出其中的Majority Element。其中Majority Element的定义为数组中出现次数大于 n / 2次的数字。
解决这个问题有以下几种思路:
1、暴力法
遍历数组中每一个元素,统计其出现的系数是否大于 n/2次,如果是就直接返回。时间复杂度o(![]() )。空间复杂度o(1);
)。空间复杂度o(1);
参考代码:
class Solution {
public:
int majorityElement(vector& nums) {
int i;
for(i = 0;i < (int)nums.size();++i) {
if(count(nums.begin(), nums.end(), nums[i]) > nums.size() / 2) { //这里使用了STL函数,count函数也会遍历整个数组,所以时间复杂度为o(n2)
break;
}
}
return nums[i];
}
}; 注:题目中说道了,保证给定的数组中一定存在着Majority Element,所以上面那样写是没有问题的,外层的for循环不会遍历完,也就是变量i不会增加到nums.size()再退出循环,如果这样的话nums[i]的下标就越界了,当然题目保证了这种情况不会发生。但是上面的代码是不能AC的,当测试集很大时,该算法超时!!
2、排序。
对输入数组先排序,那么 索引 n/2 处对应的元素一定是Majority Element,直接返回即可。时间复杂度o(nlgn),空间复杂度o(1)。
AC代码:
class Solution {
public:
int majorityElement(vector& nums) {
sort(nums.begin(), nums.end());
return nums[nums.size() / 2];
}
}; 3、随机法。
由于Majority Element出现的次数大于 n/2那么每次随机从nums中选取一个数有大于1/2的概率选中Majority Element,所以我们可以随机选取一个索引,然后统计其出现的次数是否大于n/2,如果是就直接返回索引处对应的值,否则继续迭代。数学期望是最多循环两次就可以得到结果了,所以时间复杂度为o(n),空间复杂度为o(1)。
AC代码:
class Solution {
public:
int majorityElement(vector& nums) {
int res = 0;
srand(time(NULL));
while(true)
{
int n = rand() % nums.size();
res = nums[n];
if(count(nums.begin(),nums.end(),res) > (nums.size() >> 1) )
break;
}
return res;
}
}; 4、分治。
每次将数组一分为二,分别统计左右两边的Majority Element,基准条件是被分成的数组只有一个元素了,那么该元素就是Majority Element,直接返回就可。如果左右两边的Majority Element相同,返回它即可,如果不相同则返回出现次数更多的那一个。
AC代码:原代码出处
class Solution {
public:
int majorityElement(vector& nums) {
return majority(nums, 0, nums.size() - 1);
}
private:
int majority(vector& nums, int left, int right) {
if (left == right)
return nums[left];
int mid = left + ((right - left) >> 1);
int lm = majority(nums, left, mid);
int rm = majority(nums, mid + 1, right);
if (lm == rm)
return lm;
return count(nums.begin() + left, nums.begin() + right + 1, lm) > count(nums.begin() + left, nums.begin() + right + 1, rm) ? lm : rm;
}
}; 时间复杂度分析:类似于归并排序,如果复杂度为T(n),显然有 T(n) = 2T(n/2) + o(n)。所以最终的时间复杂度为o(nlgn)。由于递归函数的调用,消耗的空间复杂度为o(![]() )。n为数组长度。
)。n为数组长度。
5、Boyer-Moore算法。
代码分为两步:1、找出一个Majority Element候选值。2、检查该候选值是否是Majority Element。由于在本题中题目已经明确存在Majority Element了,所以第二步可以省略。
找出候选者的方法:
初始化候选值为数组中的任一元素(为了方便直接初始化为首元素),初始化变量count为1。遍历数组,如果等于候选值,count++,或者count--。当count == 0时,给候选值赋值为当前遍历值。
In python:
candidate = 0
count = 0
for value in input:
if count == 0:
candidate = value
if candidate == value:
count += 1
else:
count -= 1In C++ AC代码:
class Solution {
public:
int majorityElement(vector& nums) {
int res = 0;
int count = 0;
for(int i = 0;i < nums.size();++i)
{
if(count == 0) {
res = nums[i];
}
if(nums[i] == res) {
count++;
} else {
count--;
}
}
return res;
}
}; 时间复杂度o(n),空间复杂度O(1)。
上面就是该题的一些解法思路,在这里还提高了一种使用位运算计算的代码,该思想与博主曾写过的一篇位运算总结里面的--给你一个非空的整数数组,里面只有一个数只出现了一次,其余的数都出现了两次,输出这个这出现一次的数字,的通用解法类似,感兴趣的可以去看看。
//2018/12/24 添加
昨天看到了一道新题,与上一题很相似。先看题目
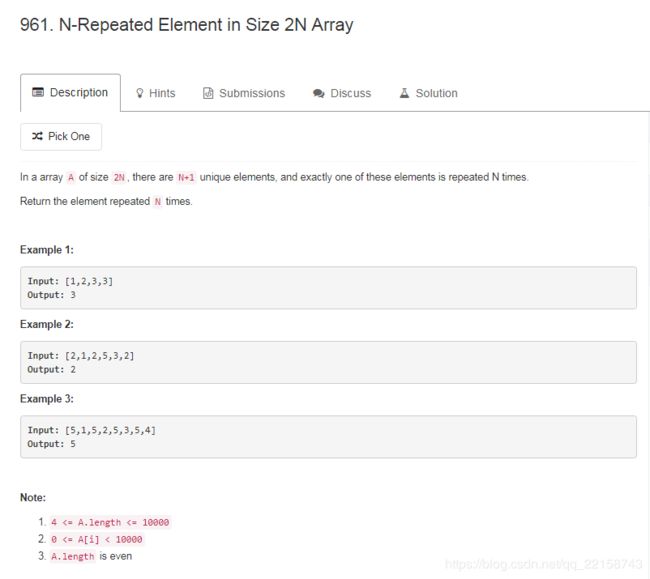
LeetCode --- 961. N-Repeated Element in Size 2N Array:
题目大意是:在一段长度为2N的整数数组中,有N+1个不同的整数,其中有一个数重复了N次,找出这个重复了N次的数字。注意到数组的长度大于等于4,小于等于10000。数组中的元素都大于等于0,小于10000;数组的长度为偶数。
与上一题的区别:1、就是在上一题中Majority Element出现的次数是大于数组长度一半的,而本题是恰好等于数组长度的一半。2、在本题中只有一个数字可以重复(重复的数字为N次),其余的数字都只能出现一次,而在上一题中除了Majority Element之外的元素也是可以重复的只要重复的次数小于N/2次即可。
首先要明确这一题不能使用Boyer-Moore算法来解决了,因为Boyer-Moore算法是用来在线性时间内找出数组中出现次数大于N/2次的,而本题的出现次数恰好是N/2次不满足要求。比如测试用例:[2,1,2,5,3,2],使用Boyer-Moore算法输出的是3,而正确的输出应该是2才对,所以本题不能使用Boyer-Moore算法。
方法一:使用hashset。
遍历数组,利用一个hashset来保存已经出现过的数字,如果该数字没有带hashset中出现则插入到hashset中,否则就直接返回该数字(因为其余的数字都不可以重复,如果出现了重复数字那么一定是我们要找的结果)。
AC代码:
class Solution {
public:
int repeatedNTimes(vector& A) {
unordered_set dict;
int num;
for(int i = 0;i < (int)A.size();++i) {
if(dict.count(A[i]) != 0) {
num = A[i];
} else {
dict.insert(A[i]);
}
}
return num;
}
}; 方法二:使用随机数法。
每次从nums中随机的选取一个数字,我们有1/2的概率选取到我们要找的数字,那么我们每次独立的选取两个数字就有1/4的概率选到的两个数字时相等的,这个数字就是我们要找的数字。
AC代码:
class Solution {
public:
int repeatedNTimes(vector& A) {
int i,j;
while (A[i = rand() % A.size()] != A[j = rand() % A.size()] || i == j);
return A[i];
}
}; 方法三:利用性质比较。
我们可以发现,重复的数字要么出现在相邻的两个数字之间(A[i],A[i+1])或者交替出现(A[i],A[i+2]),只有一种情况例外,比如【2,1,3,2】在这种情况下我们返回最后一个数字即可。
AC代码:
class Solution {
public:
int repeatedNTimes(vector& A) {
if(A[0] == A[1]) {
return A[0];
}
for(int i = 2;i < (int)A.size();++i) {
if(A[i] == A[i - 2] || A[i] == A[i - 1]) {
return A[i];
}
}
return A.back();
}
}; LeetCode---229. Majority Element II
与上一题不同的是,本题是找出出现次数大于 n/3 次的数。易知,一个数组中出现n/3次的数可能有一个也可能有两个。本题使用的算法是基于Boyer-Moore算法的扩展。
AC代码:
class Solution {
public:
vector majorityElement(vector& nums) {
vector res;
if(nums.empty()) {
return res;
}
int count1 = 0;
int count2 = 0;
int candidate1 = nums.front();
int candidate2 = nums.front();
for(int i = 0;i < (int)nums.size();++i) {
if(nums[i] == candidate1) {
count1++;
} else if(nums[i] == candidate2) {
count2++;
} else if(count1 == 0) {
candidate1 = nums[i];
count1 = 1;
} else if(count2 == 0) {
candidate2 = nums[i];
count2 = 1;
} else {
count1--;
count2--;
}
}
if(count(nums.begin(),nums.end(),candidate1) > nums.size() / 3) {
res.push_back(candidate1);
}
if(count(nums.begin(),nums.end(),candidate2) > nums.size() / 3 && candidate1 != candidate2) {
res.push_back(candidate2);
}
return res;
}
}; 可以发现使用这用思路可以线性时间内查找出现 n/k 次的元素,只需要再增加几个候选项即可。
参考:
JAVA-------------------Easy Version To Understand!!!!!!!!!!!!
Majority Voting Algorithm Find the majority element in a list of values
不是吹,这年头很少有我这么写注释的了
6 Suggested Solutions in C++ with Explanations
Boyer-Moore Majority Vote algorithm and my elaboration
C++ 2 lines O(4) | O (1)