GBDT原理与Sklearn源码分析-分类篇

摘要：

继上一篇文章，介绍完回归任务下的GBDT后，这篇文章将介绍在分类任务下的GBDT，大家将可以看到，对于回归和分类，其实GBDT过程简直就是一模一样的。如果说最大的不同的话，那就是在于由于loss function不同而引起的初始化不同、叶子节点取值不同。

正文：

GB的一些基本原理都已经在上文中介绍了，下面直接进入正题。
下面是分类任务的GBDT算法过程，其中选用的loss function是logloss。
L(yi,Fm(xi))=−{yilogpi+(1−yi)log(1−pi)} L ( y i , F m ( x i ) ) = − { y i l o g p i + ( 1 − y i ) l o g ( 1 − p i ) } 。
其中 pi=11+e(−Fm(xi)) p i = 1 1 + e ( − F m ( x i ) )

---

这里简单推导一下logloss通常化简后的式子：
L(yi,Fm(xi))=−{yilogpi+(1−yi)log(1−pi)} L ( y i , F m ( x i ) ) = − { y i l o g p i + ( 1 − y i ) l o g ( 1 − p i ) }
（先不带入负号）
带入 pi p i => yilog(11+e(−Fm(xi)))+(1−yi)log(e(−Fm(xi))1+e(−Fm(xi))) y i l o g ( 1 1 + e ( − F m ( x i ) ) ) + ( 1 − y i ) l o g ( e ( − F m ( x i ) ) 1 + e ( − F m ( x i ) ) )
=> −yilog(1+e(−Fm(xi)))+(1−yi){log(e(−Fm(xi)))−log(1+e(−Fm(xi)))} − y i l o g ( 1 + e ( − F m ( x i ) ) ) + ( 1 − y i ) { l o g ( e ( − F m ( x i ) ) ) − l o g ( 1 + e ( − F m ( x i ) ) ) }
=> −yilog(1+e(−Fm(xi)))+log(e(−Fm(xi)))−log(1+e(−Fm(xi)))−yilog(e(−Fm(xi)))+yilog(1+e(−Fm(xi))) − y i l o g ( 1 + e ( − F m ( x i ) ) ) + l o g ( e ( − F m ( x i ) ) ) − l o g ( 1 + e ( − F m ( x i ) ) ) − y i l o g ( e ( − F m ( x i ) ) ) + y i l o g ( 1 + e ( − F m ( x i ) ) )
=> yiFm(xi)−log(1+eFm(xi)) y i F m ( x i ) − l o g ( 1 + e F m ( x i ) )
最后加上负号可以得：
L(yi,Fm(xi))=−{yilogpi+(1−yi)log(1−pi)}=−{yiFm(xi)−log(1+eFm(xi))} L ( y i , F m ( x i ) ) = − { y i l o g p i + ( 1 − y i ) l o g ( 1 − p i ) } = − { y i F m ( x i ) − l o g ( 1 + e F m ( x i ) ) }

---

Algorithm 3:BinomiaDeviance_TreeBoost____________________________________F0(x)=0.5∗log(∑Ni=1yi∑Ni=1(1−yi))From=1 to M do:       yi~=−[∂L(yi,F(xi))∂F(xi)]F(x)=Fm−1(x)=yi−11+e(−Fm−1(xi))       {Rjm}J1=J−terminal node tree({ỹ i,xi}N1)       γjm=∑xi∈Rjmỹ i∑xi∈Rjm(yi−ỹ i)∗(1−yi+ỹ i)       Fm(x)=Fm−1(x)+∑j=1JγjmI(x∈Rjm) A l g o r i t h m   3 : B i n o m i a D e v i a n c e _ T r e e B o o s t _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ F 0 ( x ) = 0.5 ∗ l o g ( ∑ i = 1 N y i ∑ i = 1 N ( 1 − y i ) ) F r o m = 1   t o   M   d o :               y i ~ = − [ ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ] F ( x ) = F m − 1 ( x ) = y i − 1 1 + e ( − F m − 1 ( x i ) )               { R j m } 1 J = J − t e r m i n a l   n o d e   t r e e ( { y ~ i , x i } 1 N )               γ j m = ∑ x i ∈ R j m y ~ i ∑ x i ∈ R j m ( y i − y ~ i ) ∗ ( 1 − y i + y ~ i )               F m ( x ) = F m − 1 ( x ) + ∑ j = 1 J γ j m I ( x ∈ R j m )

算法3就是GBDT用于分类任务时，loss funcion选用logloss的算法流程。
可以看到，和回归任务是一样的，并没有什么特殊的处理环节。
（其实在sklearn源码里面，虽然回归任务的模型定义是GradientBoostingRegressor()而分类任务是GradientBoostingClassifier()，但是这两者区分开来是为了方便用户使用，最终两者都是共同继承BaseGradientBoosting()，算法3这些流程都是在BaseGradientBoosting()完成的，GradientBoostingRegressor()、GradientBoostingClassifier()只是完成一些学习器参数配置的任务）

实践

下面同样以一个简单的数据集来大致的介绍一下GBDT的过程。

xi x i	1	2	3	4	5	6	7	8	9	10
yi y i	0	0	0	1	1	0	0	0	1	1

---

参数配置：
1. 以logloss为损失函数
2. 以MSE为分裂准则
3. 树的深度为1
4. 学习率为0.1

---

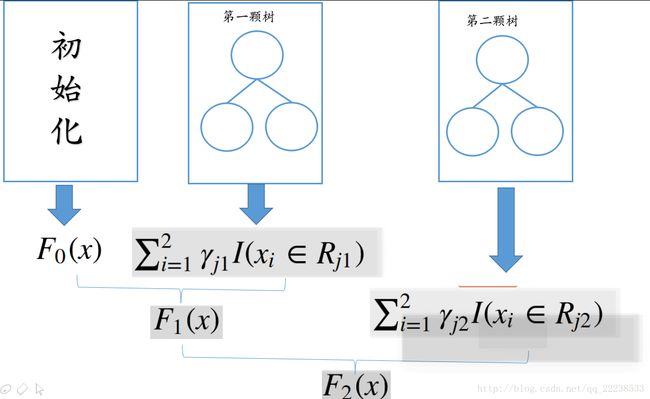
算法3的第一步，初始化。
F0(x)=log(∑Ni=1yi∑Ni=1(1−yi))=log(46)=−0.4054 F 0 ( x ) = l o g ( ∑ i = 1 N y i ∑ i = 1 N ( 1 − y i ) ) = l o g ( 4 6 ) = − 0.4054

---

拟合第一颗树( m=1 m = 1 )
计算负梯度值：
yi~=−[∂L(yi,F(xi))∂F(xi)]F(x)=Fm−1(x)=yi−11+e(−Fm−1(xi))=yi−11+e(−F0(xi)) y i ~ = − [ ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ] F ( x ) = F m − 1 ( x ) = y i − 1 1 + e ( − F m − 1 ( x i ) ) = y i − 1 1 + e ( − F 0 ( x i ) )

比如计算第一个样本( i=1 i = 1 )有：
y1~=0−11+e(0.4054)=−0.400 y 1 ~ = 0 − 1 1 + e ( 0.4054 ) = − 0.400
同样地，其他计算后如下表：

xi x i	1	2	3	4	5	6	7	8	9	10
ỹ i y ~ i	-0.4	-0.4	-0.4	0.6	0.6	-0.4	-0.4	-0.4	0.6	0.6

接着，我们需要以 ỹ i y ~ i 为目标，拟合一颗树。
拟合树的过程上篇文章已经详细介绍了，这里就不再累述了。拟合完后结果如下：

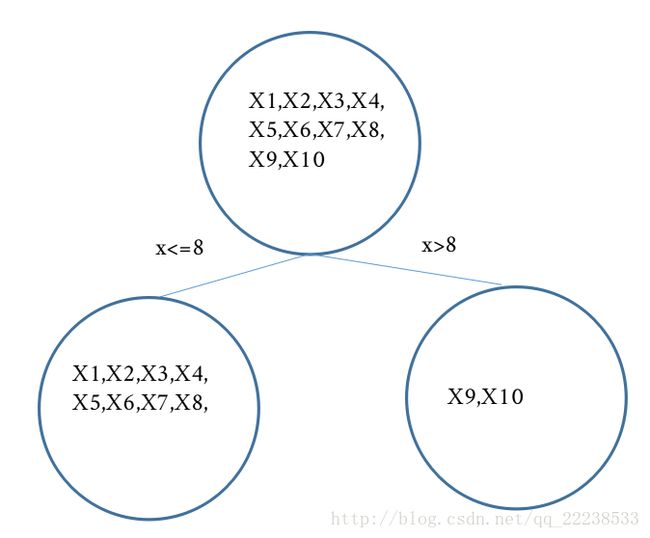
可以得出建好树之后叶子节点的区域：
R11 R 11 为 xi<=8 x i <= 8 ， R21 R 21 为 xi>8 x i > 8
下面计算可以叶子节点的值 γjm γ j m
由公式： γjm=∑xi∈Rjmỹ i∑xi∈Rjm(yi−ỹ i)∗(1−yi+ỹ i) γ j m = ∑ x i ∈ R j m y ~ i ∑ x i ∈ R j m ( y i − y ~ i ) ∗ ( 1 − y i + y ~ i )
对于区域 R11 R 11 有如下：
∑xi∈R11ỹ i=(ỹ 1+ỹ 2+ỹ 3+ỹ 4+ỹ 5+ỹ 6+ỹ 7+ỹ 8)=−1.2 ∑ x i ∈ R 11 y ~ i = ( y ~ 1 + y ~ 2 + y ~ 3 + y ~ 4 + y ~ 5 + y ~ 6 + y ~ 7 + y ~ 8 ) = − 1.2
∑xi∈R11(yi−ỹ i)∗(1−yi+ỹ i)=(y1−ỹ 1)∗(1−y1+ỹ 1)+(y2−ỹ 2)∗(1−y2+ỹ 2)+(y3−ỹ 3)∗(1−y3+ỹ 3)+(y4−ỹ 4)∗(1−y4+ỹ 4)+(y5−ỹ 5)∗(1−y5+ỹ 5)+(y6−ỹ 6)∗(1−y6+ỹ 6)+(y7−ỹ 7)∗(1−y7+ỹ 7)+(y8−ỹ 8)∗(1−y8+ỹ 8)=1.92 ∑ x i ∈ R 11 ( y i − y ~ i ) ∗ ( 1 − y i + y ~ i ) = ( y 1 − y ~ 1 ) ∗ ( 1 − y 1 + y ~ 1 ) + ( y 2 − y ~ 2 ) ∗ ( 1 − y 2 + y ~ 2 ) + ( y 3 − y ~ 3 ) ∗ ( 1 − y 3 + y ~ 3 ) + ( y 4 − y ~ 4 ) ∗ ( 1 − y 4 + y ~ 4 ) + ( y 5 − y ~ 5 ) ∗ ( 1 − y 5 + y ~ 5 ) + ( y 6 − y ~ 6 ) ∗ ( 1 − y 6 + y ~ 6 ) + ( y 7 − y ~ 7 ) ∗ ( 1 − y 7 + y ~ 7 ) + ( y 8 − y ~ 8 ) ∗ ( 1 − y 8 + y ~ 8 ) = 1.92

对于区域 R21 R 21 有如下：
∑xi∈R21ỹ i=(ỹ 9+ỹ 10)=1.2 ∑ x i ∈ R 21 y ~ i = ( y ~ 9 + y ~ 10 ) = 1.2
∑xi∈R21(yi−ỹ i)∗(1−yi+ỹ i)=(y9−ỹ 9)∗(1−y9+ỹ 9)+(y10−ỹ 10)∗(1−y10+ỹ 10)=0.48 ∑ x i ∈ R 21 ( y i − y ~ i ) ∗ ( 1 − y i + y ~ i ) = ( y 9 − y ~ 9 ) ∗ ( 1 − y 9 + y ~ 9 ) + ( y 10 − y ~ 10 ) ∗ ( 1 − y 10 + y ~ 10 ) = 0.48

故最后可以得到两个叶子节点的值：
γ11=−1.21.92=−0.625 γ 11 = − 1.2 1.92 = − 0.625 、 γ21=1.20.480=2.5 γ 21 = 1.2 0.480 = 2.5

最后通过 Fm(x)=Fm−1(x)+∑Jj=1γjmI(x∈Rjm) F m ( x ) = F m − 1 ( x ) + ∑ j = 1 J γ j m I ( x ∈ R j m ) 更新 F1(x) F 1 ( x ) ，需要注意的是，这里同样也用shrinkage，即乘一个学习率 η η ，具体表现为：
Fm(x)=Fm−1(x)+η∗∑Jj=1γjmI(x∈Rjm) F m ( x ) = F m − 1 ( x ) + η ∗ ∑ j = 1 J γ j m I ( x ∈ R j m ) 。

以计算 x1 x 1 为例：
F1(x1)=F0(x1)+0.1∗(−0.625)=−0.4054−0.0625=−0.4679 F 1 ( x 1 ) = F 0 ( x 1 ) + 0.1 ∗ ( − 0.625 ) = − 0.4054 − 0.0625 = − 0.4679
其他计算完毕后如下表供参考：

xi x i	1	2	3	4	5	6	7	8	9	10
F1(xi) F 1 ( x i )	-0.46796511	-0.46796511	-0.46796511	-0.46796511	-0.46796511	-0.46796511	-0.46796511	-0.46796511	-0.15546511	-0.15546511

至此，第一颗树已经训练完成。可以再次看到其训练过程和回归基本没有区别。

---

下面简单提一下拟合第二颗树( m=2) m = 2 )

计算负梯度值：
比如对于 x1 x 1 有：
=> ỹ 1=y1−11+e(−F1(x1))=0−0.38509=−0.38509 y ~ 1 = y 1 − 1 1 + e ( − F 1 ( x 1 ) ) = 0 − 0.38509 = − 0.38509
其他同理，可得下表：

xi x i	1	2	3	4	5	6	7	8	9	10
ỹ i y ~ i	-0.38509799	-0.38509799	-0.38509799	0.61490201	0.61490201	-0.38509799	-0.38509799	-0.38509799	0.53878818	0.53878818

之后也是以新的 ỹ i y ~ i 为目标拟合一颗回归树后计算叶子节点的区间和叶子节点的值。

---

关于预测

当只有2颗树的时候，其预测过程也是和下面这个图一样

相比于回归任务，分类任务需把要最后累加的结果 Fm(x) F m ( x ) 转成概率。（其实 Fm(x) F m ( x ) 可以理解成一个得分）。具体来说：
对于采用logloss作为损失函数的情况下， pi=11+e(−Fm(xi)) p i = 1 1 + e ( − F m ( x i ) ) 。
对于采用指数损失作为损失函数的情况下， pi=11+e(−2Fm(xi)) p i = 1 1 + e ( − 2 F m ( x i ) ) 。
当然这里的 pi p i 指的是正样本的概率。

这里再详细一点，比如对于上面例子，当我们拟合完第二颗树后，计算 F2(x) F 2 ( x ) 可有有下表：

xi x i	1	2	3	4	5	6	7	8	9	10
F2(xi) F 2 ( x i )	-0.52501722	-0.52501722	-0.52501722	-0.52501722	-0.52501722	-0.52501722	-0.52501722	-0.52501722	0.06135501	0.06135501

此时计算相应的概率值有：
F2(x) F 2 ( x ) 可有有下表：

xi x i	1	2	3	4	5	6	7	8	9	10
pi p i	0.37167979	0.37167979	0.37167979	0.37167979	0.37167979	0.37167979	0.37167979	0.37167979	0.51533394	0.51533394

(表中的概率为正样本的概率，即 yi=1 y i = 1 的概率）

Sklearn源码简单分析

写在前面：Sklearn源码分析后面有时间有添加一些内容，下面先简单了解GDBT分类的核心代码。

---

当loss function选用logloss时，对应的是sklearn里面的loss=’deviance’。
计算负梯度、初始化、更新叶子节点、转成概率都在一个名叫BinomialDeviance()的类中。

class BinomialDeviance(ClassificationLossFunction):
    """Binomial deviance loss function for binary classification.

    Binary classification is a special case; here, we only need to
    fit one tree instead of ``n_classes`` trees.
    """
    def __init__(self, n_classes):
        if n_classes != 2:
            raise ValueError("{0:s} requires 2 classes.".format(
                self.__class__.__name__))
        # we only need to fit one tree for binary clf.
        super(BinomialDeviance, self).__init__(1)

    def init_estimator(self):
        return LogOddsEstimator()

    def __call__(self, y, pred, sample_weight=None):
        """Compute the deviance (= 2 * negative log-likelihood). """
        # logaddexp(0, v) == log(1.0 + exp(v))
        pred = pred.ravel()
        if sample_weight is None:
            return -2.0 * np.mean((y * pred) - np.logaddexp(0.0, pred))
        else:
            return (-2.0 / sample_weight.sum() *
                    np.sum(sample_weight * ((y * pred) - np.logaddexp(0.0, pred))))

    def negative_gradient(self, y, pred, **kargs):
        """Compute the residual (= negative gradient). """
        return y - expit(pred.ravel())

    def _update_terminal_region(self, tree, terminal_regions, leaf, X, y,
                                residual, pred, sample_weight):
        """Make a single Newton-Raphson step.

        our node estimate is given by:

            sum(w * (y - prob)) / sum(w * prob * (1 - prob))

        we take advantage that: y - prob = residual
        """
        terminal_region = np.where(terminal_regions == leaf)[0]
        residual = residual.take(terminal_region, axis=0)
        y = y.take(terminal_region, axis=0)
        sample_weight = sample_weight.take(terminal_region, axis=0)

        numerator = np.sum(sample_weight * residual)
        denominator = np.sum(sample_weight * (y - residual) * (1 - y + residual))
        # prevents overflow and division by zero
        if abs(denominator) < 1e-150:
            tree.value[leaf, 0, 0] = 0.0
        else:
            tree.value[leaf, 0, 0] = numerator / denominator

    def _score_to_proba(self, score):
        proba = np.ones((score.shape[0], 2), dtype=np.float64)
        proba[:, 1] = expit(score.ravel())
        proba[:, 0] -= proba[:, 1]
        return proba

    def _score_to_decision(self, score):
        proba = self._score_to_proba(score)
        return np.argmax(proba, axis=1)

下面这是用于计算负梯度值。注意的函数expit就是 11+e−x 1 1 + e − x
代码中的y_pred或者pred表达的就是 Fm−1(x) F m − 1 ( x )

    def negative_gradient(self, y, pred, **kargs):
        """Compute the residual (= negative gradient). """
        return y - expit(pred.ravel())

更新叶子节点，关键在于计算numerator和denominator。
另外代码里的residual代表的是负梯度值。

    def _update_terminal_region(self, tree, terminal_regions, leaf, X, y,
                                residual, pred, sample_weight):
        """Make a single Newton-Raphson step.

        our node estimate is given by:

            sum(w * (y - prob)) / sum(w * prob * (1 - prob))

        we take advantage that: y - prob = residual
        """
        terminal_region = np.where(terminal_regions == leaf)[0]
        residual = residual.take(terminal_region, axis=0)
        y = y.take(terminal_region, axis=0)
        sample_weight = sample_weight.take(terminal_region, axis=0)

        numerator = np.sum(sample_weight * residual)
        denominator = np.sum(sample_weight * (y - residual) * (1 - y + residual))
        # prevents overflow and division by zero
        if abs(denominator) < 1e-150:
            tree.value[leaf, 0, 0] = 0.0
        else:
            tree.value[leaf, 0, 0] = numerator / denominator

初始化的类：

class LogOddsEstimator(object):
    """An estimator predicting the log odds ratio."""
    scale = 1.0

    def fit(self, X, y, sample_weight=None):
        # pre-cond: pos, neg are encoded as 1, 0
        if sample_weight is None:
            pos = np.sum(y)
            neg = y.shape[0] - pos
        else:
            pos = np.sum(sample_weight * y)
            neg = np.sum(sample_weight * (1 - y))

        if neg == 0 or pos == 0:
            raise ValueError('y contains non binary labels.')
        self.prior = self.scale * np.log(pos / neg)

    def predict(self, X):
        check_is_fitted(self, 'prior')

        y = np.empty((X.shape[0], 1), dtype=np.float64)
        y.fill(self.prior)
        return y

其中，下面这个用于初始化，可以看到有一个因子self.scale，这是由于在Sklearn里提供两种loss function用于分类，一种是logloss，一种是指数损失，两者的初始化仅仅只是在系数上不同，前者是1.0,后者是0.5。

    def fit(self, X, y, sample_weight=None):
        # pre-cond: pos, neg are encoded as 1, 0
        if sample_weight is None:
            pos = np.sum(y)
            neg = y.shape[0] - pos
        else:
            pos = np.sum(sample_weight * y)
            neg = np.sum(sample_weight * (1 - y))

        if neg == 0 or pos == 0:
            raise ValueError('y contains non binary labels.')
        self.prior = self.scale * np.log(pos / neg)

最后是转化成概率，这里有个细节，就是正样本的概率是放在第2列（从1数起）。

    def _score_to_proba(self, score):
        proba = np.ones((score.shape[0], 2), dtype=np.float64)
        proba[:, 1] = expit(score.ravel())
        proba[:, 0] -= proba[:, 1]
        return proba

总结

至此，GBDT用于回归和分类的两种情况都已经说明完毕，欠缺的可能是源码部分说的不够深入，由于最近时间的关系没办法做到太深入，所以后面找时间会把代码再深入的分析后补充在这。

对于多分类问题也需要单独讨论详细请看文章。

参考资料

http://docplayer.net/21448572-Generalized-boosted-models-a-guide-to-the-gbm-package.html（各种loss function的推导结果）
http://xueshu.baidu.com/s?wd=paperuri%3A%28ab7165108163edc94b30781e51819e0c%29&filter=sc_long_sign&sc_ks_para=q%3DGreedy%20function%20approximation%3A%20A%20gradient%20boosting%20machine.&sc_us=13783016239361402484&tn=SE_baiduxueshu_c1gjeupa&ie=utf-8 （本文主要参考的超级著名论文 greedy function approximation: a gradient boosting machine）