阵列信号基础之1:MUSIC 算法
无线信道参数估计算法
对通信系统分析之前,首先需要建立一个能够完整反映该系统的传输信道的模型,其模型中的参数包括接收端接收信号的时延,发射端和接收端的联合方向分布等,获取这些参数的过程就是无线信道参数估计的过程。
方法可以大致分为三类:
- 谱估计算法:多重信号分类法
- 参数子空间估计算法:旋转不变技术估计信号参数算法
- 确定性参数估计算法:期望最大算法以及演进的空间交替广义期望最大算法
0. 前言
阵列信号处理基础本质上属于参数估计问题,和信道估计知识基本上别无二致。末学在这里整理了阵列信号处理的基础知识。
1. 多重信号分类法
MUSIC 算法原理
MUSIC 算法,叫做多信号分类算法 (Multiple Signal classification)。MUSIC 算法的基本思想是将任意阵列输出数据的协方差矩阵进行特征分解,从而得到与信号分量相对应的信号子空间和信号分量相正交的噪声子空间,然后利用这两个子空间的正交性来估计信号的参数 (入射方向、极化信息和信号强度)。MUSIC 算法是一种高分辨率的、高精度的无线信道参数估计算法,而且该算法对于天线阵列的形状没有特殊要求,具有普遍的适用性,只要已知天线阵的布阵形式,无论是直线阵列还是圆阵列,不管阵元是否是等间距分布,都可以得到高分辨率的结果。但是该算法对于入射信号的要求非常高,应用该算法的前提是入射信号必须是互不相干的。
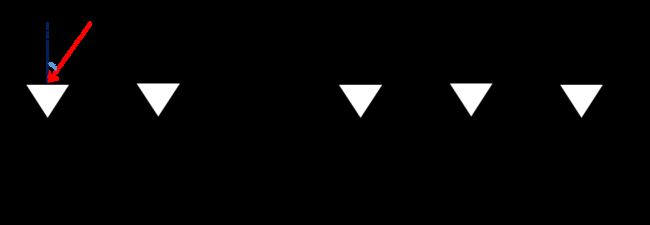
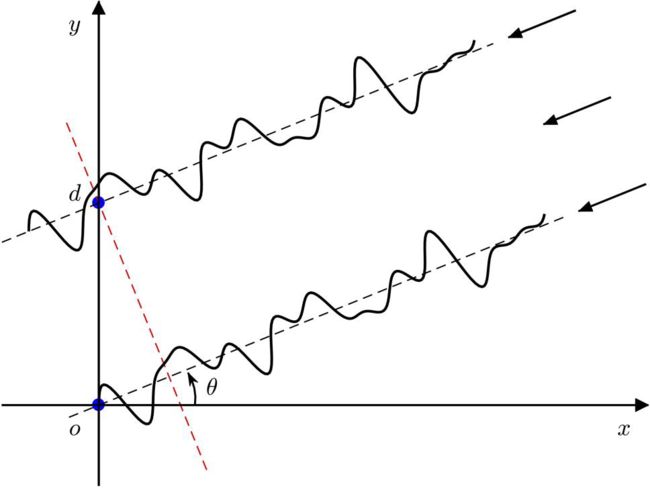
考虑由 N N N 个阵元组成的均匀线性阵列 (Uniform Linear Array),阵列之间的间距为半波长 d = λ / 2 d=\lambda/2 d=λ/2,假设有 M M M 个远场信号源,它们的功率相同且互不相干,分别从不同的方向入射到接收阵列,其中入射信号和噪声互不相关。以最左侧的阵元为参考点,各个阵元的位置相比前一个增加距离 d d d。信号入射方向角为 θ \theta θ,表示入射信号与线阵法线的夹角。一般假设信号源数 M M M 小于阵元数目 N N N。
在第 k k k 次快拍,得到的接收数据向量为:
X ( k ) = A ( θ ) S ( k ) + N ( k ) , k = 1 , 2 , ⋯ , K \boxed{ X(k)=A(\theta)S(k)+N(k),k=1,2,\cdots,K } X(k)=A(θ)S(k)+N(k),k=1,2,⋯,K
其中, A ( θ ) = [ a ( θ 1 ) , a ( θ 2 ) , ⋯ , a ( θ M ) ] A(\theta)=\left[ a(\theta_1),a(\theta_2),\cdots,a(\theta_M)\right] A(θ)=[a(θ1),a(θ2),⋯,a(θM)] 是 N × M N\times M N×M 的阵列矩阵,又称为阵列流形向量或者方向响应向量。 S ( k ) = [ s 1 ( k ) , s 2 ( k ) , ⋯ , s M ( k ) ] T S(k)=\left[ s_1(k),s_2(k),\cdots,s_M(k)\right]^T S(k)=[s1(k),s2(k),⋯,sM(k)]T 是 M M M 个入射信号矢量。
X ( k ) = [ x 1 ( k ) , x 2 ( k ) , ⋯ , x N ( k ) ] T X(k)=\left[ x_1(k),x_2(k),\cdots,x_N(k)\right]^T X(k)=[x1(k),x2(k),⋯,xN(k)]T 是 N N N 个输出信号矢量。
N ( k ) = [ n 1 ( k ) , n 2 ( k ) , ⋯ , n N ( k ) ] T N(k)=\left[ n_1(k),n_2(k),\cdots,n_N(k)\right]^T N(k)=[n1(k),n2(k),⋯,nN(k)]T 是阵列噪声矢量。
一般假设噪声为加性高斯即: E ( n i ( k ) ) = 0 , E ( n i ( k ) n i ( k ) H ) = σ 2 I \mathbb{E}(n_i(k))=0,\quad \mathbb{E}(n_i(k)n_i(k)^H)=\sigma^2I E(ni(k))=0,E(ni(k)ni(k)H)=σ2I。
阵列矩阵的元素满足:
a ( θ i ) = [ 1 , e − j 2 π d sin θ i / λ , ⋯ , e − j ( N − 1 ) 2 π d sin θ i / λ ] a(\theta_i)=\left[1,e^{-j2\pi d \sin{\theta_i}/ \lambda},\cdots,e^{-j(N-1)2\pi d \sin{\theta_i}/ \lambda} \right] a(θi)=[1,e−j2πdsinθi/λ,⋯,e−j(N−1)2πdsinθi/λ]
其中, λ \lambda λ 是中心波长, θ i \theta_i θi 为信号源的入射角。因此,问题转化为对 X X X 进行多点采样,通过对采样的输出信号 X ( k ) X(k) X(k) 估计出信号源的波达方向角 θ i \theta_i θi。
由上图中两束方向确定的信号发射到两个不同阵元,在同一时刻采样的信号值为随机值,待估的方向一定。于是,输出信号的协方差矩阵可以表示为:
R X X = E [ X ( k ) X ( k ) H ] = E [ A ( θ ) S ( k ) S ( k ) H A ( θ ) H ] + E [ N ( k ) N ( k ) H ] = A ( θ ) E [ S ( k ) S ( k ) H ] A ( θ ) H + R N = A R S A H + σ 2 I \begin{aligned} R_{XX}&=\mathbb{E}\left[X(k)X(k)^H \right] \\ &=\mathbb{E}\left[A(\theta)S(k)S(k)^HA(\theta)^H \right]+\mathbb{E}\left[N(k)N(k)^H \right]\\ &=A(\theta)\color{#F00}{\mathbb{E}\left[S(k)S(k)^H \right]}A(\theta)^H+R_N\\ &=A\color{#F00}{R_S}A^H+\sigma^2I \end{aligned} RXX=E[X(k)X(k)H]=E[A(θ)S(k)S(k)HA(θ)H]+E[N(k)N(k)H]=A(θ)E[S(k)S(k)H]A(θ)H+RN=ARSAH+σ2I
其中 R S R_S RS 是输入信号的协方差矩阵。由于信号和噪声相互独立,数据协方差可分解为信号子空间和噪声子空间。由于 R X X R_{XX} RXX 是对称矩阵,然后我们对其进行特征值分解,得到
R X X = U Σ U H = U S Σ S U S H + U N Σ N U N H R_{XX}=U \Sigma U^H = U_{S} \Sigma_{S}\ U_{S}^{H}+U_{N} \Sigma_{N} U_{N}^{H} RXX=UΣUH=USΣS USH+UNΣNUNH
其中 U = [ U S , U N ] U=\left[ U_S,U_N\right] U=[US,UN], Σ = diag ( σ 1 2 , ⋯ , σ N 2 ) \Sigma = \text{diag} \left( \sigma_{1}^2,\cdots,\sigma_{N}^2 \right) Σ=diag(σ12,⋯,σN2), U S U_S US 是由大的特征值对应的特征向量张成的子空间,即信号子空间。 U N U_N UN 是由小的特征值对应的特征矢量张成的子空间,即为噪声子空间。
Σ = [ Σ S Σ N ] = [ λ 1 λ 2 ⋱ λ N ] , where λ 1 ⩾ λ 2 ⩾ ⋯ ⩾ λ M > λ M + 1 = ⋯ = λ N = σ 2 , Σ S = [ λ 1 λ 2 ⋱ λ M ] , Σ N = [ λ M + 1 λ M + 2 ⋱ λ N ] . \Sigma =\begin{bmatrix} \Sigma_{S}& \\ &\Sigma_{N} \end{bmatrix} = \begin{bmatrix} \lambda_{1}&&& \\ & \lambda_{2}&& \\&&\ddots& \\&&& \lambda_{N} \end{bmatrix},\\ \text{where} \quad \lambda_{1} \geqslant \lambda_{2} \geqslant \cdots \geqslant \lambda_{M} > \lambda_{M+1}= \cdots = \lambda_{N}=\sigma^{2}, \\ \Sigma_{S} = \begin{bmatrix} \lambda_{1}&&& \\ & \lambda_{2}&& \\&&\ddots& \\&&& \lambda_{M} \end{bmatrix},\\ \Sigma_{N} = \begin{bmatrix} \lambda_{M+1}&&& \\ & \lambda_{M+2}&& \\&&\ddots& \\&&& \lambda_{N} \end{bmatrix}. Σ=[ΣSΣN]=⎣⎢⎢⎡λ1λ2⋱λN⎦⎥⎥⎤,whereλ1⩾λ2⩾⋯⩾λM>λM+1=⋯=λN=σ2,ΣS=⎣⎢⎢⎡λ1λ2⋱λM⎦⎥⎥⎤,ΣN=⎣⎢⎢⎡λM+1λM+2⋱λN⎦⎥⎥⎤.
由于信号子空间和噪声子空间是相互正交的,有
R X X U N = [ U S , U N ] Σ [ U S H U N H ] U N = [ U S , U N ] Σ [ 0 I ] = [ U S , U N ] [ σ S 2 σ N 2 ] [ 0 I ] = σ N 2 U N \begin{aligned} R_{XX}U_N &=\left[ U_S,U_N\right] \Sigma \color{#F00}{\begin{bmatrix} U^H_S\\ U^H_N \end{bmatrix}U_N} \\ &=\left[ U_S,U_N\right] \Sigma \color{#F00}{\begin{bmatrix} \mathbf{0}\\ I \end{bmatrix} } \\ &=\left[ U_S,U_N\right] {\begin{bmatrix} \sigma_{S}^2& \\ &\sigma_{N}^2 \end{bmatrix} } {\begin{bmatrix} \mathbf{0}\\ I \end{bmatrix} } \\ &=\sigma_{N}^2U_N \end{aligned} RXXUN=[US,UN]Σ[USHUNH]UN=[US,UN]Σ[0I]=[US,UN][σS2σN2][0I]=σN2UN
结合 R X X U N = A R S A H U N + σ 2 I U N = σ N 2 U N R_{XX} U_N=A{R_S}A^HU_N+\sigma^2IU_N=\sigma_{N}^2U_N RXXUN=ARSAHUN+σ2IUN=σN2UN 成立,可得
A R S A H U N = 0 U N H A R S A H U N = ( A H U N ) H R S A H U N = 0 \boxed{A{R_S}A^HU_N=\mathbf{0} }\\ U_N^{H}A{R_S}A^HU_N=\left(A^HU_N\right)^{H}{R_S}A^HU_N=\mathbf{0} ARSAHUN=0UNHARSAHUN=(AHUN)HRSAHUN=0
因为 A ≠ 0 , R S ≠ 0 A \neq 0, \ R_S \neq \mathbf{0} A=0, RS=0,可推出上式的充分必要条件: A H U N = 0 A^HU_N=\mathbf{0} AHUN=0。这个性质也可以从另外一方面说明,已知模型为 X = A S + N X=AS+N X=AS+N,在无噪声情况下的信号 x ( t ) = ∑ i = 1 M s i ( t ) a i ( θ ) → x ( t ) ∈ span { a 1 , a 2 , ⋯ , a M } x(t) = \sum_{i=1}^{M}s_i(t)a_i(\theta) \rightarrow x(t) \in \text{span}\{a_1,a_2,\cdots,a_M\} x(t)=∑i=1Msi(t)ai(θ)→x(t)∈span{a1,a2,⋯,aM}。协方差矩阵大特征值对应的特征向量张成的空间与入射信号的导向矢量张成的空间是同一个空间,即
U S = [ e 1 , e 2 , ⋯ , e M ] , U N = [ e M + 1 , e M + 2 , ⋯ , e N ] , span { e 1 , e 2 , ⋯ , e M } = span { a 1 , a 2 , ⋯ , a M } . U_S=\left[ e_1,e_2,\cdots,e_M\right], \quad U_N=\left[ e_{M+1},e_{M+2},\cdots,e_N\right], \\ \text{span}\{ e_1,e_2,\cdots,e_M\}=\text{span}\{a_1,a_2,\cdots,a_M\}. US=[e1,e2,⋯,eM],UN=[eM+1,eM+2,⋯,eN],span{e1,e2,⋯,eM}=span{a1,a2,⋯,aM}.
信号子空间和噪声子空间是相互正交,可知信号子空间的导向矢量 A ( θ ) A(\theta) A(θ) 和噪声子空间也正交,即
a H ( θ ) U N = 0 , θ = { θ 1 , θ 2 , ⋯ , θ M } . \mathbf{a}^H(\theta)U_N=\mathbf{0},\quad \theta=\{\theta_1,\theta_2,\cdots,\theta_M\}. aH(θ)UN=0,θ={θ1,θ2,⋯,θM}.
然而实际采集的接收数据矩阵有限长,首先获取输入信号的大量釆样值 X = { x 1 , x 2 , ⋯ , x K } X= \{ x_1,x_2, \cdots, x_K \} X={x1,x2,⋯,xK},进而可以估计输入信号的协方差矩阵,达到极大似然估计的目的:
R ^ x = 1 K ∑ 1 K x k x k H \hat{R}_x=\frac{1}{K}\sum_{1}^{K}x_kx_k^H R^x=K11∑KxkxkH
其中, K K K 是快拍数,然后对 R ^ x \hat{R}_x R^x 特征值分解: R ^ x = U ^ Σ U ^ H \hat{R}_x=\hat{U} {\Sigma} \hat{U}^H R^x=U^ΣU^H。同理得到两个子空间:
R ^ x = U ^ Σ U ^ H = U ^ S Σ S U ^ S H + U ^ N Σ N U ^ N H \begin{aligned} \hat{R}_x &=\hat{U} {\Sigma} \hat{U}^H \\ &= \hat{U}_{S} \Sigma_{S}\ \hat{U}_{S}^{H}+\hat{U}_{N} \Sigma_{N} \hat{U}_{N}^{H} \end{aligned} R^x=U^ΣU^H=U^SΣS U^SH+U^NΣNU^NH
由于实际的干扰因素, a H ( θ ) U N = 0 \mathbf{a}^H(\theta)U_N=\mathbf{0} aH(θ)UN=0 不完全成立,即不会完全满足正交性。这里采用最小优化搜索来估计波达方向:
θ M U S I C = arg min θ a H ( θ ) U ^ N U ^ N H a ( θ ) \theta_{MUSIC}=\underset{\theta}{\text{arg min}} \ \ \mathbf{a}^H(\theta) \hat{U}_N \hat{U}^H_N \mathbf{a}(\theta) θMUSIC=θarg min aH(θ)U^NU^NHa(θ)
从上式可以看出,由于阵列方向向量与噪声子空间正交的缘故,信号入射方向上会出现极小值。通过上式整理得到空间谱函数,进行极大值的谱峰搜索,可得
P M U S I C ( θ ) = 1 a H ( θ ) U ^ N U ^ N H a ( θ ) P_{MUSIC}(\theta) =\frac{1}{\mathbf a^{H}(\theta) \hat{\mathbf U}_{N} \hat {\mathbf U}_{N}^{H}\mathbf a(\theta)} PMUSIC(θ)=aH(θ)U^NU^NHa(θ)1
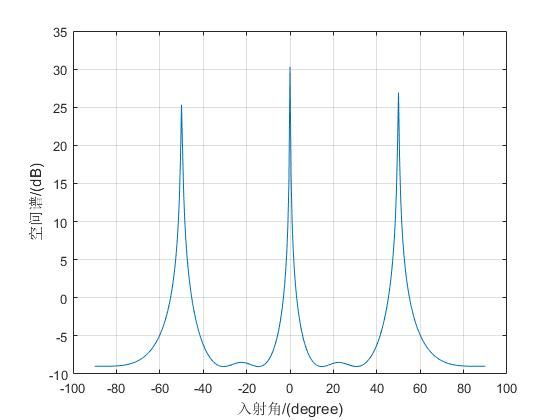
MUSIC 实验仿真
clc; clear; close all;
%%%%%%%%%%%%%%%%%% MUSIC %%%%%%%%%%%%%%%%%%
derad = pi/180;
N = 8; % 阵元个数
M = 3; % 信源数目
theta = [-50 0 50]; % 待估计角度
snr = 10; % 信噪比
K = 1024; % 快拍数 10/1024
dd = 0.5; % 阵元间距 d=lamda/2
d=0:dd:(N-1)*dd;
A=exp(-1i*2*pi*d.'*sin(theta*derad));
S=randn(M,K); X=A*S;
X1=awgn(X,snr,'measured');
Rxx=X1*X1'/K;
%InvS=inv(Rxx);
[EV,D]=eig(Rxx); % 特征向量 特征值
EVA=diag(D)';
[EVA,I]=sort(EVA); % 从小到大排列 返回索引
%EVA=fliplr(EVA); % 反转元素
EV=fliplr(EV(:,I)); % 按列反转特征向量
for iang = 1:361 % 遍历
angle(iang)=(iang-181)/2;
phim=derad*angle(iang);
a=exp(-1i*2*pi*d*sin(phim)).';
L=M;
En=EV(:,L+1:N);
%SP(iang)=(a'*a)/(a'*En*En'*a);
SP(iang)=1/(a'*En*En'*a);
end
SP=abs(SP);
%SPmax=max(SP);
%SP=10*log10(SP/SPmax); % 归一化
SP=10*log10(SP);
h=plot(angle,SP);
set(h,'Linewidth',0.5);
xlabel('入射角/(degree)');
ylabel('空间谱/(dB)');
%axis([-100 100 -40 60]);
set(gca, 'XTick',[-100:20:100]);
grid on;
ROOT-MUSIC 算法
基本的算法中,结果的精度与扫描的精度直接相关,增大扫描精度也即要减小扫描间隔,也即用运算量来换取精度。求根算法是对 MUSIC 基本算法的演进,降低运算量。在求根算法中可以用多项式求根的方法来替代算法中的谱峰搜索。考虑以下模型:
X ( k ) = A ( θ ) S ( k ) + ξ ( k ) , k = 1 , 2 , ⋯ , K \boxed{ X(k)=A(\theta)S(k)+\xi(k),k=1,2,\cdots,K } X(k)=A(θ)S(k)+ξ(k),k=1,2,⋯,K
在基本算法中,数据协方差矩阵是可以分解为相互正交的信号子空间和噪声子空间。阵列矩阵投影到噪声子空间,并在角度功率谱上进行谱峰搜索。现定义 z = exp ( j 2 π d sin θ / λ ) z=\exp(j2\pi d \sin \theta/ \lambda) z=exp(j2πdsinθ/λ),则阵列矩阵转化为:
a ( θ i ) = [ 1 , e − j 2 π d sin θ i / λ , ⋯ , e − j ( N − 1 ) 2 π d sin θ i / λ ] T = [ 1 , e j 2 π d sin θ i / λ , ⋯ , e j ( N − 1 ) 2 π d sin θ i / λ ] H = [ 1 , z ( θ i ) , ⋯ , z N − 1 ( θ i ) ] H \begin{aligned} a(\theta_i)&=\left[1,e^{-j2\pi d \sin{\theta_i}/ \lambda},\cdots,e^{-j(N-1)2\pi d \sin{\theta_i}/ \lambda} \right]^T \\ &=\left[1,e^{j2\pi d \sin{\theta_i}/ \lambda},\cdots,e^{j(N-1)2\pi d \sin{\theta_i}/ \lambda} \right]^{\color{red}H} \\ &=\left[1,z(\theta_i),\cdots,z^{N-1}(\theta_i) \right]^{\color{red} H} \end{aligned} a(θi)=[1,e−j2πdsinθi/λ,⋯,e−j(N−1)2πdsinθi/λ]T=[1,ej2πdsinθi/λ,⋯,ej(N−1)2πdsinθi/λ]H=[1,z(θi),⋯,zN−1(θi)]H
结合子空间 U N = [ e M + 1 , e M + 2 , ⋯ , e N ] U_N=\left[ e_{M+1},e_{M+2},\cdots,e_N\right] UN=[eM+1,eM+2,⋯,eN],极大值的谱峰搜索函数可以改写为:
P M U S I C − 1 ( θ ) = f ( z ) = a H ( θ ) U N U N H a ( θ ) = [ 1 , z ( θ i ) , ⋯ , z N − 1 ( θ i ) ] [ e M + 1 , e M + 2 , ⋯ , e N ] [ e M + 1 , e M + 2 , ⋯ , e N ] H [ 1 , z ( θ i ) , ⋯ , z N − 1 ( θ i ) ] H = p H ( z ) U N U N H p ( z ) \begin{aligned} P_{MUSIC}^{-1}(\theta) = f(z) &= \mathbf a^{H}(\theta) {\mathbf U}_{N} {\mathbf U}_{N}^{H}\mathbf a(\theta) \\ &= \left[1,z(\theta_i),\cdots,z^{N-1}(\theta_i) \right] \left[ e_{M+1},e_{M+2},\cdots,e_N\right] \\ &\left[ e_{M+1},e_{M+2},\cdots,e_N\right]^{H} \left[1,z(\theta_i),\cdots,z^{N-1}(\theta_i) \right]^{H} \\ & = \mathbf{p}^H(z) {\mathbf U}_{N} {\mathbf U}_{N}^{H} \mathbf{p}(z) \end{aligned} PMUSIC−1(θ)=f(z)=aH(θ)UNUNHa(θ)=[1,z(θi),⋯,zN−1(θi)][eM+1,eM+2,⋯,eN][eM+1,eM+2,⋯,eN]H[1,z(θi),⋯,zN−1(θi)]H=pH(z)UNUNHp(z)
令 f ( z ) = 0 f(z)=0 f(z)=0,求得该多项式的根即为到达角的信息。但是该多项式存在共轭项 z ∗ z^* z∗,因此修正上式为:
f ( z ) = p H ( z ) U N U N H p ( z ) = z N − 1 p T ( z − 1 ) U N U N H p ( z ) = q ( z ) U N U N H p ( z ) , where q ( z ) = [ z N − 1 , z N − 2 , ⋯ , 1 ] . \begin{aligned} f(z) & = \mathbf{p}^{\color{#F00}H}(z) {\mathbf U}_{N} {\mathbf U}_{N}^{H} \mathbf{p}(z) \\ & = z^{N-1}\mathbf{p}^{\color{#F00}T}(z^{-1}) {\mathbf U}_{N} {\mathbf U}_{N}^{H} \mathbf{p}(z) \\ & = \mathbf{q}(z){\mathbf U}_{N} {\mathbf U}_{N}^{H} \mathbf{p}(z), \\ \end{aligned} \\ \text{where} \quad \mathbf{q}(z) = \left[z^{N-1},z^{N-2},\cdots,1\right]. f(z)=pH(z)UNUNHp(z)=zN−1pT(z−1)UNUNHp(z)=q(z)UNUNHp(z),whereq(z)=[zN−1,zN−2,⋯,1].
基于以上变换,推导 f ( z ) f(z) f(z) 的展开式:
f ( z ) = q ( z ) U N U N H p ( z ) , = q ( e M + 1 e M + 1 ∗ , e M + 2 e M + 2 ∗ , ⋯ , e N e N ∗ ) p ( z ) = [ z N − 1 , z N − 2 , ⋯ , 1 ] [ b 11 ⋱ b N N ] [ 1 z ⋮ z N − 1 ] = [ ( z N − 1 b 11 + z N − 2 b 21 + ⋯ + b N 1 ) , ⋯ , ( z N − 1 b 1 N + z N − 2 b 2 N + ⋯ + b N N ) ] [ 1 z ⋮ z N − 1 ] = ( z N − 1 b 11 + z N − 2 b 21 + ⋯ + b N 1 ) + ⋯ + ( z N − 1 b 1 N + z N − 2 b 2 N + ⋯ + b N N ) z N − 1 = b N 1 + ( b N − 1 , 1 + b N 2 ) z + ⋯ + b 1 N z 2 ( N − 1 ) f(z) = \mathbf{q}(z){\mathbf U}_{N} {\mathbf U}_{N}^{H} \mathbf{p}(z), \\ =\mathbf{q}\left(e_{M+1}e_{M+1}^*,e_{M+2}e_{M+2}^*,\cdots,e_Ne_{N}^* \right) \mathbf{p}(z) \\ = \left[z^{N-1},z^{N-2},\cdots,1\right] \begin{bmatrix} b_{11}&& \\ &\ddots& \\ &&b_{NN} \end{bmatrix} \begin{bmatrix} 1 \\ z \\ \vdots \\ z^{N-1} \end{bmatrix} \\ =\left[ \left(z^{N-1}b_{11}+z^{N-2}b_{21}+\cdots+b_{N1} \right),\cdots, \\ \left(z^{N-1}b_{1N}+z^{N-2}b_{2N}+\cdots+b_{NN} \right) \right] \begin{bmatrix} 1 \\ z \\ \vdots \\ z^{N-1} \end{bmatrix} \\ = \left(z^{N-1}b_{11}+z^{N-2}b_{21}+\cdots+b_{N1} \right)+\cdots \\ +\left(z^{N-1}b_{1N}+z^{N-2}b_{2N}+\cdots+b_{NN} \right) z^{N-1} \\ = \color{red}{b_{N1}+(b_{N-1,1}+b_{N2})z+\cdots+b_{1N}z^{2(N-1)}} f(z)=q(z)UNUNHp(z),=q(eM+1eM+1∗,eM+2eM+2∗,⋯,eNeN∗)p(z)=[zN−1,zN−2,⋯,1]⎣⎡b11⋱bNN⎦⎤⎣⎢⎢⎢⎡1z⋮zN−1⎦⎥⎥⎥⎤=[(zN−1b11+zN−2b21+⋯+bN1),⋯,(zN−1b1N+zN−2b2N+⋯+bNN)]⎣⎢⎢⎢⎡1z⋮zN−1⎦⎥⎥⎥⎤=(zN−1b11+zN−2b21+⋯+bN1)+⋯+(zN−1b1N+zN−2b2N+⋯+bNN)zN−1=bN1+(bN−1,1+bN2)z+⋯+b1Nz2(N−1)
f ( z ) f(z) f(z) 是阶数为 2 ( N − 1 ) 2(N-1) 2(N−1) 次幂的多项式,因此根据代数基本定理:任何一个非零的一元 n n n 次复系数多项式,都正好有 n n n 个复数根。也就是说 f ( z ) f(z) f(z) 有 ( N − 1 ) (N-1) (N−1) 对共轭根,根据定义 z = exp ( j 2 π d sin θ / λ ) z=\exp(j2\pi d \sin \theta/ \lambda) z=exp(j2πdsinθ/λ) 可知,当根满足定义时, p ( z ) \mathbf{p}(z) p(z) 为导向矢量,且根正好在单位圆上(模为1),其中有 M M M 个根正好在单位圆上。因此,对于接近于单位圆上的根进行求解:
θ i = arcsin ( λ 2 π d arg { z ^ } ) , i = 1 , 2 , ⋯ , M . where arg { exp ( j w ) } = w . \boxed{\theta_{i} = \arcsin \left( \frac{\lambda}{2\pi d} \arg\{\hat{z}\} \right), \ \ i=1,2,\cdots,M.\\ \text{where} \quad \arg\{\exp(jw)\}=w.} θi=arcsin(2πdλarg{z^}), i=1,2,⋯,M.wherearg{exp(jw)}=w.
仿真代码如下:
%ROOT_MUSIC ALOGRITHM %DOA ESTIMATION BY ROOT_MUSIC
clc; clear; close all;
K=2; %信源数
M=8; %阵元数
L=200; %信号长度
w=[pi/4 pi/6].'; %信号频率
lamda=((2*pi*3e8)/w(1)+(2*pi*3e8)/w(2))/2; %信号波长
d_lamda=0.5; %阵元间距
snr=20; %信噪比
theta1=[45,60]; %信号入射角
for k=1:K
A(:,k)=exp(-1j*[0:M-1]'*d_lamda*2*pi*sin(theta1(k)*pi/180)); %阵列流型
end
for kk=1:L
s(:,kk)=sqrt(10.^((snr/2)/10))*exp(1j*w*(kk-1)); %仿真信号
end
x=A*s+(1/sqrt(2))*(randn(M,L)+1j*randn(M,L)); %加入高斯白噪声
R=(x*x')/L; %协方差矩阵
%%%%%%第一种方法%%%%%%%%%%
[V,D]=eig(R); %对协方差矩阵进行特征分解
Un=V(:,1:M-K); %取噪声子空间
Gn=Un*Un';
a = zeros(2*M-1,1)'; %找出多项式的系数,并按阶数从高至低排列
for i=-(M-1):(M-1)
a(i+M) = sum(diag(Gn,i));
end
a1=roots(a); %使用ROOTS函数求出多项式的根
a2=a1(abs(a1)<1); %找出在单位圆里且最接近单位圆的N个根
[lamda,I]=sort(abs(abs(a2)-1)); %挑选出最接近单位圆的N个根
f=a2(I(1:K)); %计算信号到达方向角
source_doa=[asin(angle(f(1))/pi)*180/pi,asin(angle(f(2))/pi)*180/pi];
source_doa=sort(source_doa);
disp('source_doa');
disp(source_doa);
%%%%%%%第二种方法%%%%%%%%%
% [V,D]=eig(R);
% Un=V(:,1:M-K); %(4.5.7)
% Un1=Un(1:M,:);
% Un2=Un(K+1:M,:);
% T=[1 0 0 0 0 0]'; %(阵元数-信源数)*1
% c=Un1*inv(Un2)*T; % (K*(M-K))*((M-K)*(M-K))*((M-K)*1)=K*1
% c=[1,c(2,1),c(1,1)]; %(4.5.8)
% f=roots(c);
% source_doa=[asin(angle(f(1))/pi)*180/pi asin(angle(f(2))/pi)*180/pi];
% source_doa=sort(source_doa);
% disp('source_doa');
% disp(source_doa);