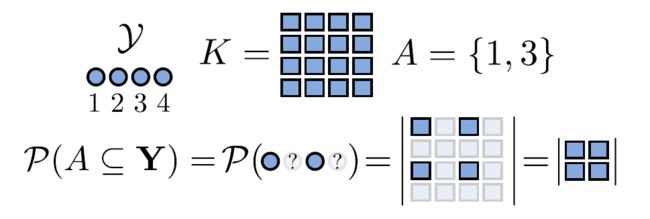Determinantal point process 入门
Determinantal point process 入门
1. 什么是“行列式点过程”
在机器学习(ML)中,子集选择问题的目标是从 ground set 中选择具有高质量但多样化的 items 的子集。这种高质量和多样性的平衡在 ML 问题中经常通过使用行列式点过程(determinantal point process,DPP)来保持,其中 DPP 赋予子集上的分布能够使得选择两个相似项的概率是(反)相关的。
虽然 DPPs 在随机几何(Stochastic Geometry,SG)中已被广泛地用于建模点间斥力(inter-point repulsion)问题,但它们对 ML 应用尤其有益,因为它们的分布参数可以从训练集中有效地学习到。
DPP 包括两个概念
- 行列式过程
- 点过程
行列式点过程 P \mathcal P P 是在一个离散的有限基本点集 Y = { 1 , 2 , ⋯ , N } \mathcal Y=\{1,2,\cdots, N\} Y={1,2,⋯,N} 的幂集 2 Y 2^{\mathcal Y} 2Y(所有子集, 包括空集和全集,构成的集合)上定义的概率分布。
幂集(Power Set):就是原集合中所有的子集(包括全集和空集)构成的集族。 设 X \mathcal X X 是一个有限集, ∣ X ∣ = k |\mathcal X| = k ∣X∣=k,则 X \mathcal X X 的幂集的势为 2 k 2^k 2k。
设 A ⊆ Y A \subseteq \mathcal Y A⊆Y 是一个固定的子集, Y Y Y 是根据 DPP 从 Y \mathcal Y Y 中随机生成的一些点构成的一个子集( Y ∼ P Y \sim \mathcal P Y∼P),则
P ( A ⊆ Y ) = det ( K A ) P(A \subseteq Y) =\det(K_A) P(A⊆Y)=det(KA)
其中 ∣ Y ∣ = N \vert \mathcal Y \vert=N ∣Y∣=N, K K K 是 similarity matrix,是 N × N N \times N N×N 的实对称半正定方阵。 K A K_A KA 是 K K K 的与 A A A 中元素在 Y \mathcal Y Y 中的标号相对应的元素构成子方阵。
一般来说, K K K 不一定需要是对称的。然而,为了简单起见,我们继续使用这个假设,而且这不是一个有影响的限制。
对于任意 A ⊆ Y A \subseteq \mathcal Y A⊆Y, P ( A ⊆ Y ) = det ( K A ) ∈ [ 0 , 1 ] P(A \subseteq Y) =\det(K_A) \in [0,1] P(A⊆Y)=det(KA)∈[0,1],因此 K K K 的所有特征值与主子式都满足处于 [ 0 , 1 ] [0,1] [0,1],由此可知 K K K 半正定( 0 ⪯ K ⪯ I \mathbf 0 \preceq K \preceq \mathbf I 0⪯K⪯I)。
主子式:任选 i i i 行 i i i 列的子方阵。注意区别于顺序主子式。
从上图也可以看出抽象的表示, K K K 也被称为边缘核,因它确定了 DPP 的边缘分布:
P ( A ⊆ Y ) = ∑ Y ′ : Y ′ ⊇ A P ( Y = Y ′ ) P(A \subseteq Y) =\sum_{Y':Y' \supseteq A} P(Y=Y') P(A⊆Y)=Y′:Y′⊇A∑P(Y=Y′)
当 A = { i } A=\{i\} A={i},有 P ( i ∈ Y ) = K i , i P(i \in Y)=K_{i,i} P(i∈Y)=Ki,i。也就是说, K K K 的对角线给出了单个元素包含于 Y Y Y( Y Y Y 中包含有单个元素的子集)的边缘概率。
且我们定义 det ( K ∅ ) = 1 \det(K_{\varnothing}) =1 det(K∅)=1,即任意一个 DPP 生成的随机过程选中的点构成的集合都包含空集。
如果 A = { i , j } A=\{i,j\} A={i,j},那么有
P ( A ⊆ Y ) = ∣ K i , i K i , j K j , i K j , j ∣ = K i , i K j , j − K i , j K j , i = P ( i ∈ Y ) P ( j ∈ Y ) − K i , j 2 \begin{aligned} P(A \subseteq Y)& = \begin{vmatrix} K_{i,i} & K_{i,j} \\ K_{j,i} & K_{j,j} \end{vmatrix} = K_{i,i} K_{j,j} - K_{i,j} K_{j,i} \\ &=P(i \in Y)P(j \in Y)-K_{i,j}^2 \end{aligned} P(A⊆Y)=∣∣∣∣Ki,iKj,iKi,jKj,j∣∣∣∣=Ki,iKj,j−Ki,jKj,i=P(i∈Y)P(j∈Y)−Ki,j2
因此,非对角元素(对称导致了 K j , i = K i , j K_{j,i} = K_{i,j} Kj,i=Ki,j)表示成对元素之间的(反)相关度量: K i , j K_{i,j} Ki,j 值越大,表示 i i i 和 j j j 越不可能同时出现。如果我们把边缘核的项看作是 Y Y Y 中成对元素之间相似性的度量,那么高度相似的元素不太可能同时出现。
相似性度量如下:
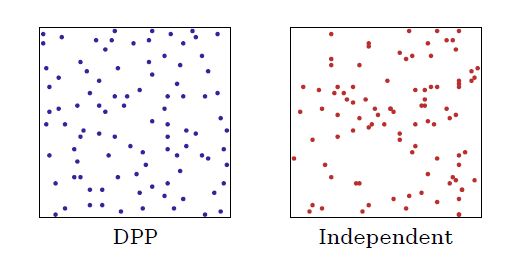
注意 K i , j K_{i,j} Ki,j 的值与点 i i i 和 j j j 之间的距离成反比。这就意味着距离越近的点越不容易成对出现。所以 DPP 采样的点比独立采样覆盖的范围更好。
例如:
例如当 K i , j = K i , i K j , j K_{i,j} = \sqrt{K_{i,i} K_{j,j}} Ki,j=Ki,iKj,j,则有 P ( { i , j } ⊆ Y ) = 0 P(\{i,j\} \subseteq Y)=0 P({i,j}⊆Y)=0 表示 { i , j } \{i,j\} {i,j} 几乎肯定不会同时出现。相反,对角元素表示没有与其他元素的相关性,因此元素独立出现。
以上就是一些大致的 DPP 概念。结合上面的图,可以理解论文中反复强调的一句话:Correlations are always negative in DPPs!
1.1 conditioning
条件概率的推导需要用到矩阵的 Schur Complement(舒尔补)参考链接;参考链接;参考链接:
若矩阵 Σ \Sigma Σ 分块如下
Σ = [ Σ 11 Σ 12 Σ 21 Σ 22 ] \Sigma = \left[ \begin{array}{cc} \Sigma_{11} & \Sigma_{12} \\ \Sigma_{21} & \Sigma_{22} \end{array} \right] Σ=[Σ11Σ21Σ12Σ22]
则存在以下关系
∣ Σ ∣ = ∣ Σ 11 − Σ 12 Σ 22 − 1 Σ 21 ∣ ∣ Σ 22 ∣ ∣ Σ ∣ = ∣ Σ 22 − Σ 21 Σ 11 − 1 Σ 12 ∣ ∣ Σ 11 ∣ \begin{aligned} \begin{vmatrix} \Sigma \end{vmatrix} &=\begin{vmatrix}\Sigma_{11}-\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21}\end{vmatrix} \begin{vmatrix}\Sigma_{22}\end{vmatrix} \\ \begin{vmatrix} \Sigma \end{vmatrix} &=\begin{vmatrix}\Sigma_{22}-\Sigma_{21}\Sigma_{11}^{-1}\Sigma_{12}\end{vmatrix} \begin{vmatrix}\Sigma_{11}\end{vmatrix} \end{aligned} ∣∣Σ∣∣∣∣Σ∣∣=∣∣Σ11−Σ12Σ22−1Σ21∣∣∣∣Σ22∣∣=∣∣Σ22−Σ21Σ11−1Σ12∣∣∣∣Σ11∣∣
这里我们命名
∣ Σ / Σ 22 ∣ = ∣ Σ 11 − Σ 12 Σ 22 − 1 Σ 21 ∣ ∣ Σ / Σ 11 ∣ = ∣ Σ 22 − Σ 21 Σ 11 − 1 Σ 12 ∣ S 22 = Σ 11 − Σ 12 Σ 22 − 1 Σ 21 S 11 = Σ 22 − Σ 21 Σ 11 − 1 Σ 12 \begin{aligned} \begin{vmatrix} \Sigma/\Sigma_{22} \end{vmatrix} &=\begin{vmatrix}\Sigma_{11}-\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21}\end{vmatrix} \\ \begin{vmatrix} \Sigma/\Sigma_{11} \end{vmatrix} &=\begin{vmatrix}\Sigma_{22}-\Sigma_{21}\Sigma_{11}^{-1}\Sigma_{12}\end{vmatrix} \\ S_{22} &= \Sigma_{11}-\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21}\\ S_{11}&=\Sigma_{22}-\Sigma_{21}\Sigma_{11}^{-1}\Sigma_{12} \end{aligned} ∣∣Σ/Σ22∣∣∣∣Σ/Σ11∣∣S22S11=∣∣Σ11−Σ12Σ22−1Σ21∣∣=∣∣Σ22−Σ21Σ11−1Σ12∣∣=Σ11−Σ12Σ22−1Σ21=Σ22−Σ21Σ11−1Σ12
这样,我们就称作 S 11 S_{11} S11 为矩阵 Σ \Sigma Σ 关于 Σ 11 \Sigma_{11} Σ11 的舒尔补。
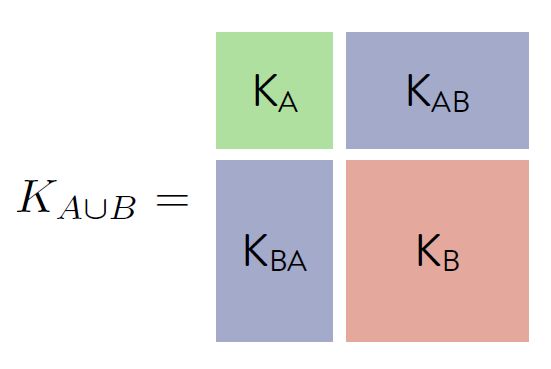
P ( B ⊆ Y ∣ A ⊆ Y ) = P ( A ∪ B ⊆ Y ) P ( A ⊆ Y ) = det ( K A ∪ B ) det ( K A ) = ∣ K B − K B A K A − 1 K A B ∣ ∣ K A ∣ ∣ K A ∣ = det ( K B − K B A K A − 1 K A B ) \begin{aligned} P(B \subseteq Y \vert A \subseteq Y ) &= \frac{P(A\cup B \subseteq Y )}{P( A \subseteq Y )} \\ &=\frac{\det(K_{A \cup B})}{\det(K_A)}= \frac{\begin{vmatrix} K_{B}-K_{BA} K_{A}^{-1} K_{AB}\end{vmatrix} \begin{vmatrix} K_{A}\end{vmatrix} }{\begin{vmatrix} K_{A}\end{vmatrix} } \\ &=\det(K_{B}-K_{BA} K_{A}^{-1} K_{AB}) \end{aligned} P(B⊆Y∣A⊆Y)=P(A⊆Y)P(A∪B⊆Y)=det(KA)det(KA∪B)=∣∣KA∣∣∣∣KB−KBAKA−1KAB∣∣∣∣KA∣∣=det(KB−KBAKA−1KAB)
2. L-ensembles
然而为了对真实数据建模,DPPs 的构造不通过边缘核函数 K K K,而通过 L-ensembles 来定义。L-ensembles 通过一个正的、半定矩阵 L L L 来定义 DPP(说白了,其实就是把 L L L 替换掉 K K K)。
P L ( Y ) ∝ det ( L Y ) P_L(Y) \propto \det(L_Y) PL(Y)∝det(LY)
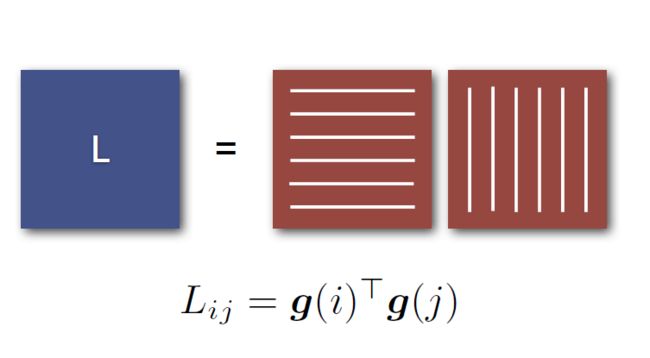
然而上面的公式只能表示一种比例关系,需要进一步归一化才能表征概率。那么怎么归一化?
首先计算
∑ Y ⊆ Y det ( L Y ) \sum_{Y \subseteq \mathcal Y} \det (L_Y) Y⊆Y∑det(LY)
在这里,借助行列式加法性质
∣ a 11 + 1 a 12 a 21 a 22 ∣ = ∣ a 11 a 12 a 21 a 22 ∣ + ∣ 1 a 12 0 a 22 ∣ \begin{aligned} \begin{vmatrix} a_{11}+1 & a_{12} \\ a_{21} & a_{22} \end{vmatrix} = \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix} + \begin{vmatrix} 1 & a_{12} \\ 0 & a_{22} \end{vmatrix} \end{aligned} ∣∣∣∣a11+1a21a12a22∣∣∣∣=∣∣∣∣a11a21a12a22∣∣∣∣+∣∣∣∣10a12a22∣∣∣∣
找到一种推理规律
det ( L + I ) = ∣ L 11 + 1 L 12 L 21 L 22 + 1 ∣ = ∣ L 11 L 12 L 21 L 22 + 1 ∣ + ∣ 1 0 L 21 L 22 + 1 ∣ = ∣ L 11 L 12 L 21 L 22 ∣ + ∣ L 11 L 12 0 1 ∣ + ∣ 1 0 L 21 L 22 ∣ + ∣ 1 0 0 1 ∣ = det ( { 1 , 2 } ) + det ( { 1 } ) + det ( { 2 } ) + det ( ∅ ) \begin{aligned} \det(L+\mathbf I) &= \begin{vmatrix} L_{11}+1 & L_{12} \\ L_{21} & L_{22}+1 \end{vmatrix} = \begin{vmatrix} L_{11} & L_{12} \\ L_{21} & L_{22}+1 \end{vmatrix} + \begin{vmatrix} 1 & 0\\ L_{21} & L_{22}+1 \end{vmatrix} \\ &=\begin{vmatrix} L_{11} & L_{12} \\ L_{21} & L_{22} \end{vmatrix} + \begin{vmatrix} L_{11} & L_{12} \\ 0 & 1 \end{vmatrix}+ \begin{vmatrix} 1 & 0\\ L_{21} & L_{22} \end{vmatrix} + \begin{vmatrix} 1 & 0 \\ 0 & 1 \end{vmatrix}\\ &= \det(\{1,2\})+ \det(\{1\})+ \det(\{2\})+ \det(\varnothing) \end{aligned} det(L+I)=∣∣∣∣L11+1L21L12L22+1∣∣∣∣=∣∣∣∣L11L21L12L22+1∣∣∣∣+∣∣∣∣1L210L22+1∣∣∣∣=∣∣∣∣L11L21L12L22∣∣∣∣+∣∣∣∣L110L121∣∣∣∣+∣∣∣∣1L210L22∣∣∣∣+∣∣∣∣1001∣∣∣∣=det({1,2})+det({1})+det({2})+det(∅)
上面两个元素可以推广到任意 N N N 个元素的情形。所以,得到
∑ Y ⊆ Y det ( L Y ) = det ( L + I ) \sum_{Y \subseteq \mathcal Y} \det (L_Y) = \det(L+\mathbf I) Y⊆Y∑det(LY)=det(L+I)
最终可以得到归一化的概率形式:
P L ( Y = Y ) = det ( L Y ) ∑ Y ⊆ Y det ( L Y ) = det ( L Y ) det ( L + I ) P_L(\mathbf Y=Y) = \frac{\det(L_Y)}{\sum_{Y \subseteq \mathcal Y} \det (L_Y) }= \frac{\det(L_Y)}{ \det(L+\mathbf I) } PL(Y=Y)=∑Y⊆Ydet(LY)det(LY)=det(L+I)det(LY)
回顾边缘核确定的 DPP 的边缘分布:
P ( A ⊆ Y ) = ∑ Y ′ ⊇ A P ( Y = Y ′ ) = det ( K A ) = ∑ Y ′ ⊇ A det ( L Y ′ ) det ( L + I ) = 1 det ( L + I ) ∑ Y ′ ⊇ A det ( L Y ′ ) \begin{aligned} P(A \subseteq \mathbf Y) &=\sum_{Y' \supseteq A} P(\mathbf Y=Y')=\det(K_A) \\ &= \sum_{Y' \supseteq A} \frac{\det(L_{Y'})}{ \det(L+\mathbf I) } = \frac{1}{ \det(L+\mathbf I) } \sum_{Y' \supseteq A} \det(L_{Y'}) \end{aligned} P(A⊆Y)=Y′⊇A∑P(Y=Y′)=det(KA)=Y′⊇A∑det(L+I)det(LY′)=det(L+I)1Y′⊇A∑det(LY′)
从上面的行列式拆分规律可知
∑ Y ′ ⊇ A det ( L Y ′ ) = det ( L + I A ˉ ) \begin{aligned} \sum_{Y' \supseteq A} \det(L_{Y'}) = \det(L+\mathbf I_{\bar A}) \end{aligned} Y′⊇A∑det(LY′)=det(L+IAˉ)
其中 I A ˉ \mathbf I_{\bar A} IAˉ 指的是:如果集合 A A A 包含索引 i i i,则 [ I A ˉ ] i i = 0 [\mathbf I_{\bar A}]_{ii}=0 [IAˉ]ii=0,而对于 i ∈ A ˉ i \in \bar A i∈Aˉ,有 [ I A ˉ ] i i = 1 [\mathbf I_{\bar A}]_{ii}=1 [IAˉ]ii=1。所以这里的 I A ˉ \mathbf I_{\bar A} IAˉ 不是单位阵。举例说明:
det ( L + I ) = ∣ L 11 L 12 L 21 L 22 ∣ + ∣ L 11 L 12 0 1 ∣ + ∣ 1 0 L 21 L 22 ∣ + ∣ 1 0 0 1 ∣ = det ( { 1 , 2 } ) + det ( { 1 } ) + det ( { 2 } ) + det ( ∅ ) i f A = { 1 } ∑ Y ′ ⊇ A det ( L Y ′ ) = det ( { 1 , 2 } ) + det ( { 1 } ) = ∣ L 11 L 12 L 21 L 22 ∣ + ∣ L 11 L 12 0 1 ∣ = ∣ L 11 L 12 L 21 L 22 + 1 ∣ = det ( [ L 11 L 12 L 21 L 22 ] + [ 0 0 0 1 ] ) \begin{aligned} \det(L+\mathbf I) &=\begin{vmatrix} L_{11} & L_{12} \\ L_{21} & L_{22} \end{vmatrix} + \begin{vmatrix} L_{11} & L_{12} \\ 0 & 1 \end{vmatrix}+ \begin{vmatrix} 1 & 0\\ L_{21} & L_{22} \end{vmatrix} + \begin{vmatrix} 1 & 0 \\ 0 & 1 \end{vmatrix}\\ &= \det(\{1,2\})+ \det(\{1\})+ \det(\{2\})+ \det(\varnothing) \\ if \quad A&=\{1\} \\ \sum_{Y' \supseteq A} \det(L_{Y'}) &= \det(\{1,2\})+ \det(\{1\}) \\ &=\begin{vmatrix} L_{11} & L_{12} \\ L_{21} & L_{22} \end{vmatrix} + \begin{vmatrix} L_{11} & L_{12} \\ 0 & 1 \end{vmatrix} =\begin{vmatrix} L_{11} & L_{12} \\ L_{21} & L_{22}+1 \end{vmatrix} \\ &=\det \left( \begin{bmatrix} L_{11} & L_{12} \\ L_{21} & L_{22} \end{bmatrix} + \begin{bmatrix} 0 & 0\\ 0 & 1 \end{bmatrix} \right) \end{aligned} det(L+I)ifAY′⊇A∑det(LY′)=∣∣∣∣L11L21L12L22∣∣∣∣+∣∣∣∣L110L121∣∣∣∣+∣∣∣∣1L210L22∣∣∣∣+∣∣∣∣1001∣∣∣∣=det({1,2})+det({1})+det({2})+det(∅)={1}=det({1,2})+det({1})=∣∣∣∣L11L21L12L22∣∣∣∣+∣∣∣∣L110L121∣∣∣∣=∣∣∣∣L11L21L12L22+1∣∣∣∣=det([L11L21L12L22]+[0001])
所以推导得到:
P ( A ⊆ Y ) = ∑ Y ′ ⊇ A P ( Y = Y ′ ) = det ( K A ) = ∑ Y ′ ⊇ A det ( L Y ′ ) det ( L + I ) = 1 det ( L + I ) ∑ Y ′ ⊇ A det ( L Y ′ ) = det ( L + I A ˉ ) det ( L + I ) = det { ( L + I A ˉ ) ( L + I ) − 1 } \begin{aligned} P(A \subseteq \mathbf Y) &=\sum_{Y' \supseteq A} P(\mathbf Y=Y')=\det(K_A) \\ &= \sum_{Y' \supseteq A} \frac{\det(L_{Y'})}{ \det(L+\mathbf I) } = \frac{1}{ \det(L+\mathbf I) } \sum_{Y' \supseteq A} \det(L_{Y'}) \\ &=\frac{\det(L+\mathbf I_{\bar A})}{ \det(L+\mathbf I) } =\det \bigg\{ (L+\mathbf I_{\bar A}) (L+\mathbf I)^{-1} \bigg\} \end{aligned} P(A⊆Y)=Y′⊇A∑P(Y=Y′)=det(KA)=Y′⊇A∑det(L+I)det(LY′)=det(L+I)1Y′⊇A∑det(LY′)=det(L+I)det(L+IAˉ)=det{(L+IAˉ)(L+I)−1}
当 A A A 等价于 Y \mathcal Y Y 的全集 { 1 , 2 , ⋯ , N } \{1,2,\cdots, N\} {1,2,⋯,N} 时,则有
det ( K ) = det { ( L + 0 ) ( L + I ) − 1 } \det(K)=\det \bigg\{ (L+\mathbf 0) (L+\mathbf I)^{-1} \bigg\} det(K)=det{(L+0)(L+I)−1}
因此得到以下推导:
K = L ( L + I ) − 1 = ( L + I − I ) ( L + I ) − 1 = I − ( L + I ) − 1 I − K = ( L + I ) − 1 ( L + I ) ( I − K ) = I L ( I − K ) + ( I − K ) = I L ( I − K ) = K L = K ( I − K ) − 1 \begin{aligned} K&=L(L+\mathbf I)^{-1} \\ &=(L+\mathbf I -\mathbf I)(L+\mathbf I)^{-1} \\ &=\mathbf I - (L+\mathbf I)^{-1} \\ \mathbf I -K &= (L+\mathbf I)^{-1} \\ (L+\mathbf I) (\mathbf I -K) &= \mathbf I \\ L(\mathbf I -K) +(\mathbf I -K) &=\mathbf I \\ L(\mathbf I -K) &= K \\ L&=K(\mathbf I -K) ^{-1} \end{aligned} KI−K(L+I)(I−K)L(I−K)+(I−K)L(I−K)L=L(L+I)−1=(L+I−I)(L+I)−1=I−(L+I)−1=(L+I)−1=I=I=K=K(I−K)−1
整理得
K = L ( L + I ) − 1 = I − ( L + I ) − 1 L = K ( I − K ) − 1 \boxed{ \begin{aligned} K&=L(L+\mathbf I)^{-1}=\mathbf I - (L+\mathbf I)^{-1} \\ L&=K(\mathbf I -K) ^{-1} \end{aligned} } KL=L(L+I)−1=I−(L+I)−1=K(I−K)−1
在这个基础上,如果存在特征值分解
L = ∑ n λ n v n v n T L=\sum_n \lambda_n \mathbf v_n \mathbf v_n^{T} L=n∑λnvnvnT
则可得到
K = ∑ n λ n λ n + 1 v n v n T K=\sum_n \frac{\lambda_n}{\lambda_n+1} \mathbf v_n \mathbf v_n^{T} K=n∑λn+1λnvnvnT
里面用到了考研常考的知识点:
如果 A A A 是对称阵,则必存在正交阵 P P P 使得
P − 1 A P = P T A P = Λ P^{-1} A P = P^{T} A P = \Lambda P−1AP=PTAP=Λ
因此可知
L = V Λ V − 1 K = L ( L + I ) − 1 = V Λ V − 1 ( V Λ V − 1 + V V − 1 ) − 1 = V Λ V − 1 V ( Λ + I ) − 1 V − 1 = V { Λ ( Λ + I ) − 1 } V − 1 \begin{aligned} L &= V\Lambda V^{-1} \\ K & =L(L+\mathbf I)^{-1} \\ &=V\Lambda V^{-1}(V\Lambda V^{-1}+V V^{-1})^{-1} \\ &=V\Lambda V^{-1} V(\Lambda+\mathbf I)^{-1} V^{-1} \\ &=V \{\Lambda (\Lambda+\mathbf I)^{-1} \} V^{-1} \end{aligned} LK=VΛV−1=L(L+I)−1=VΛV−1(VΛV−1+VV−1)−1=VΛV−1V(Λ+I)−1V−1=V{Λ(Λ+I)−1}V−1
3. Elementary DPPs
定义:如果 K K K 的每个特征值 λ \lambda λ 都在 { 0 , 1 } \{0,1\} {0,1} 中,那么 DPPs 就是 elementary 的。
定义 { v n } n ∈ V \{\mathbf v_n\}_{n \in V} {vn}n∈V 是一组标准正交向量基。具有以下特征值分解的 K K K(有些特征值为 1,有些特征值为 0):
K V = ∑ n ∈ V v n v n T K^V=\sum_{ n \in V} \mathbf v_n \mathbf v_n^{T} KV=n∈V∑vnvnT
我们将具备以上 K V K^V KV 的 DPP 记为 P V \mathcal P^V PV。一般 elementary DPPs 不是 L-ensembles。如果 Y Y Y 是服从 elementary DPPs P V \mathcal P^V PV,那么集合的 cardinality 记作 ∣ Y ∣ \vert Y \vert ∣Y∣。接下来,我们证明 elementary DPPs 具有固定的 cardinality。
首先有以下关系:
E ( ∣ Y ∣ ) = ∑ n I ( i ∈ Y ) = ∑ n K n n V = t r ( K V ) = ∑ n ∈ V ∥ v n ∥ 2 = ∣ V ∣ \begin{aligned} \mathbb E(\vert Y \vert) &=\sum_n \mathbb I(i\in Y)= \sum_n K^V_{nn} \\ &=\mathrm{tr}(K^V) =\sum_{ n \in V} \Vert \mathbf v_n \Vert^2 =\vert V \vert \end{aligned} E(∣Y∣)=n∑I(i∈Y)=n∑KnnV=tr(KV)=n∈V∑∥vn∥2=∣V∣
结合 rank ( K V ) = ∣ V ∣ ⟹ P ( ∣ Y ∣ > ∣ V ∣ ) = 0 \text{rank}(K^V)=\vert V \vert \Longrightarrow P(\vert Y \vert>\vert V \vert)=0 rank(KV)=∣V∣⟹P(∣Y∣>∣V∣)=0,因此可知 P ( ∣ Y ∣ = ∣ V ∣ ) = 1 P(\vert Y \vert=\vert V \vert)=1 P(∣Y∣=∣V∣)=1。
3.1 Sampling lemma
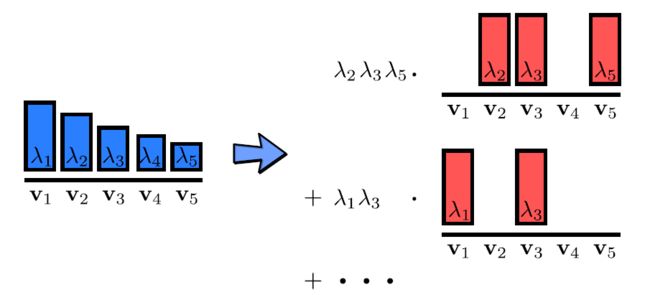
If P L P_L PL is a DPP with eigendecomposition of L L L given by L = ∑ n λ n v n v n T L=\sum_n \lambda_n \mathbf v_n \mathbf v_n^{T} L=∑nλnvnvnT. Then P L P_L PL is a mixture of elementary DPPs:
4. 偏好性-相似性分解
在大多数实际情况下,我们希望 diversity 与 Y \mathcal Y Y 中对 different items 的一些基本偏好相平衡。因此对 DPP 进行分解。这里称为 quality-diversity decomposition(偏好性-相似性分解)。
在这里 DPP kernel L L L 可以写成 Gramian 矩阵(Gram 矩阵 ;参考)的形式:
L = B T B B i = q i ϕ i L=B^T B\\ B_i=q_i \phi_i L=BTBBi=qiϕi
- q i ∈ R + q_i \in \mathbb R^{+} qi∈R+ 表示 quality,用以作为衡量 item i i i 的 “goodness” 程度。
- ϕ i ∈ R D \phi_i \in \mathbb R^{D} ϕi∈RD 表示 diversity feature vector。且 ∥ ϕ i ∥ 2 = 1 \Vert \phi_i \Vert^2=1 ∥ϕi∥2=1。虽然 D = N D = N D=N 可以分解任意的 DPP,但由于在实际中我们可能希望使用高维特征向量,所以 D D D 是任意的。
- B ∈ R D × N B \in \mathbb R^{D \times N} B∈RD×N
- S ∈ R N × N S \in \mathbb R^{N \times N} S∈RN×N
L i , j = q i ϕ i T ϕ j q j = q i S i , j q j L_{i,j}=q_i \phi_i^T \phi_j q_j =q_i S_{i,j} q_j Li,j=qiϕiTϕjqj=qiSi,jqj
- ϕ i T ϕ i = S i , i = 1 \phi_i^T \phi_i = S_{i,i} =1 ϕiTϕi=Si,i=1
- L i , i = q i ϕ i T ϕ i q i = q i S i , i q i = q i 2 L_{i,i}=q_i \phi_i^T \phi_i q_i =q_i S_{i,i} q_i=q_i^2 Li,i=qiϕiTϕiqi=qiSi,iqi=qi2
S i , j = q i ϕ i T ϕ j q j q i q j = L i , j L i , i L j , j ∈ [ − 1 , 1 ] S_{i,j}=\frac{q_i \phi_i^T \phi_j q_j }{q_i q_j }= \frac{L_{i,j} }{\sqrt{L_{i,i} L_{j,j}} } \in[-1,1] Si,j=qiqjqiϕiTϕjqj=Li,iLj,jLi,j∈[−1,1]
由于 ∥ ϕ i ∥ 2 = 1 \Vert \phi_i \Vert^2=1 ∥ϕi∥2=1,因此内积 ϕ i T ϕ j \phi_i^T \phi_j ϕiTϕj 表示两个向量的夹角余弦。
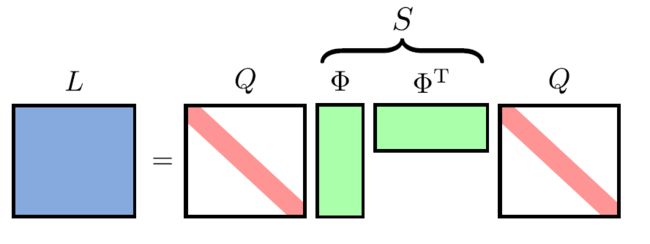
可以直接推出
P L ( Y ) ∝ det ( S Y ) ⎵ d i v e r s i t y ∏ i ∈ Y q i 2 ⎵ q u a l i t y P_L(Y) \propto \underbrace{\det(S_Y)}_{\rm diversity } \underbrace{\prod_{i \in Y} q_i^2}_{\rm quality} PL(Y)∝diversity det(SY)quality i∈Y∏qi2
4.1 对偶表示
大多数 DPP 算法需要通过 inversion、eigendecomposition 等方法对 L L L ( N × N N \times N N×N 矩阵)进行处理。然而,当 N N N 很大时,计算效率很低。因此,我们可以通过以下对偶的表示:
C = B B T C=B B^T C=BBT
在这里 C C C 是 D × D D \times D D×D 矩阵。
- C C C 和 L L L 有相同的非零特征值。
- C C C 和 L L L 的特征向量线性相关。
命题:
C C C 存在以下特征值分解
C = ∑ n = 1 D λ n v ^ n v ^ n T C=\sum_{n=1}^{D} \lambda_n \hat\mathbf v_n \hat\mathbf v_n^{T} C=n=1∑Dλnv^nv^nT
当且仅当 L L L 存在以下特征值分解
L = B T B = B T ( ∑ n = 1 D v ^ n v ^ n T ) B = ∑ n = 1 D λ n [ 1 λ n B T v ^ n ] [ 1 λ n v ^ n T B ] = ∑ n = 1 D λ n [ 1 λ n B T v ^ n ] [ 1 λ n B T v ^ n ] T \begin{aligned} L&=B^TB=B^T\left(\sum_{n=1}^{D} \hat\mathbf v_n \hat\mathbf v_n^{T}\right)B \\ &= \sum_{n=1}^{D} \lambda_n \left[\frac{1}{\sqrt{ \lambda_n}} B^T\hat\mathbf v_n \right] \left[\frac{1}{\sqrt{ \lambda_n}} \hat\mathbf v_n^{T} B\right] \\ &= \sum_{n=1}^{D} \lambda_n \left[\frac{1}{\sqrt{ \lambda_n}} B^T\hat\mathbf v_n \right] \left[\frac{1}{\sqrt{ \lambda_n}} B^T\hat\mathbf v_n\right]^T \end{aligned} L=BTB=BT(n=1∑Dv^nv^nT)B=n=1∑Dλn[λn1BTv^n][λn1v^nTB]=n=1∑Dλn[λn1BTv^n][λn1BTv^n]T
当 D D D 也特别大时,采用投影到低维( d ≪ D d \ll D d≪D)空间:
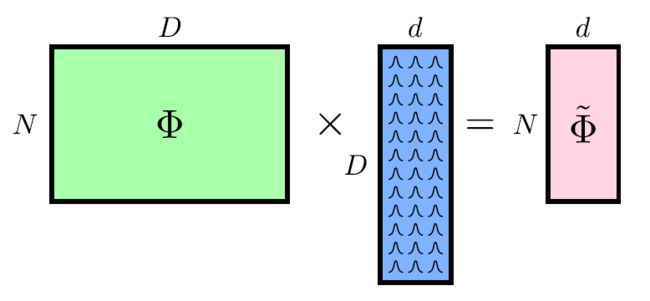
Random projections are known to approximately preserve distances [Johnson and Lindenstrauss, 1984].
5. Conditional-DPP
在很多实际问题中,固定的 ground set Y \mathcal Y Y 是不够用的。例如在 document summarization problems 中。
解决方法是找到一种取决于输入变量 X X X 的 Y ( X ) \mathcal Y(X) Y(X)。因此可以得到定义:
一种 Conditional-DPP P ( Y = Y ∣ X ) \mathcal P(\mathbf Y=Y \vert X) P(Y=Y∣X) 是一种在每一种子集 Y ⊆ Y ( X ) Y \subseteq \mathcal Y(X) Y⊆Y(X) 上的分布
P ( Y = Y ∣ X ) ∝ det ( L Y ( X ) ) \mathcal P(\mathbf Y=Y \vert X) \propto \det\Big(L_Y(X)\Big) P(Y=Y∣X)∝det(LY(X))
其中 L ( X ) L(X) L(X) 是取决于 X X X的 半正定核。利用 quality-diversity decomposition:
L i , j ( X ) = q i ( X ) ϕ i T ( X ) ϕ j ( X ) q j ( X ) = q i ( X ) S i , j ( X ) q j ( X ) L_{i,j}(X)=q_i(X) \phi_i^T(X) \phi_j(X) q_j (X)=q_i (X)S_{i,j}(X) q_j(X) Li,j(X)=qi(X)ϕiT(X)ϕj(X)qj(X)=qi(X)Si,j(X)qj(X)
在这里 Supervised learning 可以用来确定联系 X X X 与 q i q_i qi 和 ϕ i \phi_i ϕi 的隐函数。
6. k-DPP
如果我们只需要 k k k 个 diverse items 呢?
- 一个最简单的思路就是将 DPP 调整到集合 cardinality k k k:
P L k ( Y ) = det ( L Y ) ∑ ∣ Y ′ ∣ = k det ( L Y ′ ) \mathcal P^k_L( Y ) = \frac{\det(L_Y)}{\sum_{\vert Y'\vert =k} \det (L_{Y'}) } PLk(Y)=∑∣Y′∣=kdet(LY′)det(LY)
引入 k k k-th elementary symmetric polynomial:
e k ( λ 1 , λ 2 , ⋯ , λ N ) = ∑ J ⊆ { 1 , ⋯ , N } ∣ J ∣ = k ∏ n ∈ J λ n e_k(\lambda_1, \lambda_2, \cdots, \lambda_N)=\sum_{ { J \subseteq \{1,\cdots,N \} \atop \vert J \vert =k } } \prod_{n\in J} \lambda_n ek(λ1,λ2,⋯,λN)=∣J∣=kJ⊆{1,⋯,N}∑n∈J∏λn
举例说明:
e 1 ( λ 1 , λ 2 , λ 3 ) = λ 1 + λ 2 + λ 3 e 2 ( λ 1 , λ 2 , λ 3 ) = λ 1 λ 2 + λ 1 λ 2 + λ 2 λ 3 e 2 ( λ 1 , λ 2 , λ 3 ) = λ 1 λ 2 λ 3 \begin{aligned} e_1(\lambda_1, \lambda_2, \lambda_3) &= \lambda_1+\lambda_2+\lambda_3 \\ e_2(\lambda_1, \lambda_2, \lambda_3) &= \lambda_1\lambda_2+\lambda_1 \lambda_2+ \lambda_2 \lambda_3 \\ e_2(\lambda_1, \lambda_2, \lambda_3) &= \lambda_1\lambda_2 \lambda_3 \end{aligned} e1(λ1,λ2,λ3)e2(λ1,λ2,λ3)e2(λ1,λ2,λ3)=λ1+λ2+λ3=λ1λ2+λ1λ2+λ2λ3=λ1λ2λ3
因此归一化的分母为
∑ ∣ Y ′ ∣ = k det ( L Y ′ ) = e k ( λ 1 , λ 2 , ⋯ , λ N ) \sum_{\vert Y'\vert =k} \det (L_{Y'}) =e_k(\lambda_1, \lambda_2, \cdots, \lambda_N) ∣Y′∣=k∑det(LY′)=ek(λ1,λ2,⋯,λN)