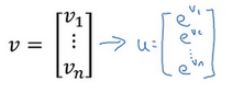【深度学习】计算的向量化(Vectorization),实现简化代码,加速计算(CPU/GPU并行计算)
当我们 应用深度学习算法,实现 大网络(网络的参数量 n n n 很大),多样本(样本数量 m m m 很大) 情形下的 大规模 计算处理时,通过 向量化 的方式,将 高度重复的计算组织成 并行的向量运算,对于 简化代码,加速运算 有着非常重要的作用。
P.S.: 本文用到的数学符号(Notation)可以参考【深度学习符号表示】
向量化简介
拿逻辑回归中 z = w T x + b z=w^Tx+b z=wTx+b 的计算举例, w w w、 x x x都是列向量,维度为 n x n_x nx。如果你有很多的特征,那么就会有一个非常大的向量。
非向量化(for循环逐个计算)做法
如果按照正常的非向量化的编程逻辑,实现思路如下(Python)。
z = 0
for i in range(n_x):
z += w[i] * x[i]
z += b
向量化做法
作为对比, w T x w^Tx wTx 的向量化计算能够非常直接地实现。
z = np.dot(w, x) + b
除了能够代码简化,向量化还能够通过并行化计算提高计算效率,我们看下面的例子。
import time # 导入时间库
import numpy as np # 导入numpy库
a = np.array([1, 2, 3, 4]) # 创建一个数据a
print(a)
# [1 2 3 4]
a = np.random.rand(1000000)
b = np.random.rand(1000000) # 通过round随机得到两个一百万维度的数组
tic = time.time() # 现在测量一下当前时间
# 向量化的版本
c = np.dot(a, b)
toc = time.time()
print(c)
print("Vectorized version:" + str(1000 * (toc - tic)) + "ms") # 打印一下向量化的版本的时间
# 继续增加非向量化的版本
c = 0
tic = time.time()
for i in range(1000000):
c += a[i] * b[i]
toc = time.time()
print(c)
print("For loop:" + str(1000 * (toc - tic)) + "ms") # 打印for循环的版本的时间
运行结果如下图:
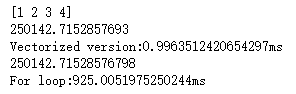
上面我们使用了向量化和非向量化两种方式进行了相同的计算,向量化版本花费了 0.996 毫秒,而非向量化版本的 for 循环花费了 925 毫秒,非向量化版本花费的时间是向量化的 900 多倍。这意味着如果向量化方法需要花费一分钟去运行的数据,使用 for 循环将会花费 15 个小时去运行。
由此可见,向量化计算有多快。
向量化计算为什么快?
你可能听过很多类似这样的话,“大规模的深度学习使用了 GPU 或者图像处理单元实现”。实际上面的示例只用了 CPU 去实现。
事实上,CPU 和 GPU 都有并行化的指令,他们有时候会叫做 SIMD 指令,这个代表了一个单独指令处理多维数据(GPU 更加擅长 SIMD 计算,CPU 虽不及 GPU,不过事实上也不是太差)。
通过调用 numpy库 或者 TensorFlow / PyTorch 等深度学习框架 中的 向量运算(线性运算)函数,我们能够让 python 充分利用 CPU 或者 GPU 的并行化计算能力。
numpy库有很多向量函数,比如
np.log() # 按元素计算对数函数
np.abs() # 按元素取绝对值
np.maximum() # 计算元素中的最大值
np.maximum(v, 0) # 计算每个元素和0相比的最大值
v ** 2 # 计算每个元素的平方
1 / v # 计算每个元素的倒数
向量化实例
① 对向量中每个元素进行数学运算
非向量化方法:初始化向量 u = n p . z e r o s ( n , 1 ) u=np.zeros(n,1) u=np.zeros(n,1),然后通过循环依次计算每个元素 v i v^{i} vi
u = np.zeros((n, 1))
for i in range(n):
u[i] = math.exp(v[i])
向量化方法:通过 python 的 numpy 内置函数 np.exp()
import numpy as np
u = np.exp(v)
② 逻辑回归的前向传播
假设我们需要对 m 个训练样本进行前向传播运算。
非向量化的做法:挨个样本进行计算,首先要对第一个样本进行预测, z ( 1 ) = w T x ( 1 ) + b z^{(1)}=w^{T}x^{(1)}+b z(1)=wTx(1)+b,计算激活函数 a ( 1 ) = σ ( z ( 1 ) ) a^{(1)}=\sigma (z^{(1)}) a(1)=σ(z(1)),再计算第一个样本的预测值 y y y。然后对第二个样本进行预测,第三个样本,依次类推。 m m m 个训练样本,就需要这样重复做 m m m 次。
向量化的做法:我们可以将训练输入定义成一个 n x n_x nx 行 m m m 列的矩阵 X X X 的形式,即一个 ( n x , m ) ( n_x,m) (nx,m)形状的numpy数组。同样,我们构建一个 1 × m 1×m 1×m 的行向量 Z Z Z 用来存储 [ z ( 1 ) , z ( m ) , . . . , z ( m ) ] [z^{(1)},z^{(m)},...,z^{(m)}] [z(1),z(m),...,z(m)],然后 Z Z Z 就可以通过下面的方式求得。
![]()
以上操作就可以通过 Z = np.dot(w.T, X) + b 一句 numpy 命令来实现。
同样的,从 Z Z Z 到 A = [ a ( 1 ) , a ( m ) , . . . , a ( m ) ] A=[a^{(1)},a^{(m)},...,a^{(m)}] A=[a(1),a(m),...,a(m)] 我们也可以使用向量方式 A = 1.0 / (1.0 + np.exp(-Z)) 来实现统一的 sigmoid函数 运算。

③ 逻辑回归的梯度下降
那么,要如何同时计算 m m m 个数据的梯度?
根据 w w w 和 b b b 的梯度计算公式:
d w = 1 m ∑ i = 1 m x ( i ) d z ( i ) dw=\frac{1}{m}\sum_{i=1}^{m}{x^{(i)}dz^{(i)}} dw=m1∑i=1mx(i)dz(i)
d b = 1 m ∑ i = 1 m d z ( i ) db=\frac{1}{m}\sum_{i=1}^{m}{dz^{(i)}} db=m1∑i=1mdz(i)
其中, d z ( 1 ) = a ( 1 ) − y ( 1 ) dz^{(1)}=a^{(1)}-y^{(1)} dz(1)=a(1)−y(1) , d z ( 2 ) = a ( 2 ) − y ( 2 ) dz^{(2)}=a^{(2)}-y^{(2)} dz(2)=a(2)−y(2)…
那么,我们可以将所有的 d z dz dz 按列堆叠(横向排列),定义一个 1 × m 1×m 1×m 形状的新的变量
d Z = [ d z ( 1 ) , d z ( 2 ) . . . d z ( m ) ] dZ=[dz^{(1)} ,dz^{(2)} ... dz^{(m)}] dZ=[dz(1),dz(2)...dz(m)]。
再定义 Y = [ y ( 1 ) , y ( 2 ) . . . y ( m ) ] Y=[y^{(1)} ,y^{(2)} ... y^{(m)}] Y=[y(1),y(2)...y(m)],则 d Z = A − Y dZ=A-Y dZ=A−Y 。
那么很容易就能得到 d b db db 的向量化代码,db = (1 / m) ∗ np.sum(A - Y)
对于 d w dw dw,为了更直观,我们先将其展开,得到
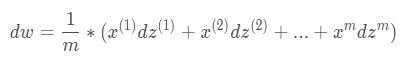
则 d w dw dw 的向量化形式, d w = 1 m ∗ X ∗ Z T dw=\frac{1}{m}*X*Z^T dw=m1∗X∗ZT,对应代码 dw = (1 / m) ∗ X * dZ.T
最终我们得到高度向量化的,高效的逻辑回归的实现
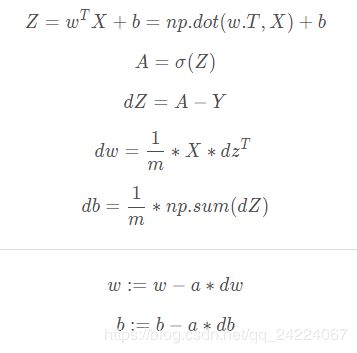
前五个公式完成前向和后向传播,后两个公式进行梯度下降更新参数。
P.S.:如果你觉得梯度的向量化计算比较困难,建议是写出一个很小很明确的向量化例子,在纸上演算梯度,然后对其一般化,得到一个高效的向量化操作形式。
吴恩达 DeepLearning.ai