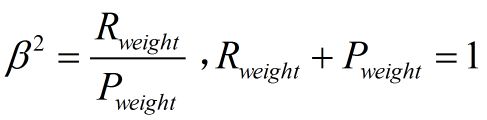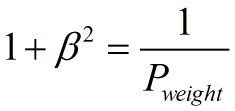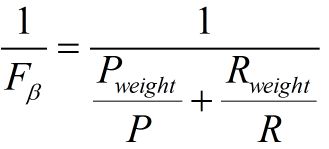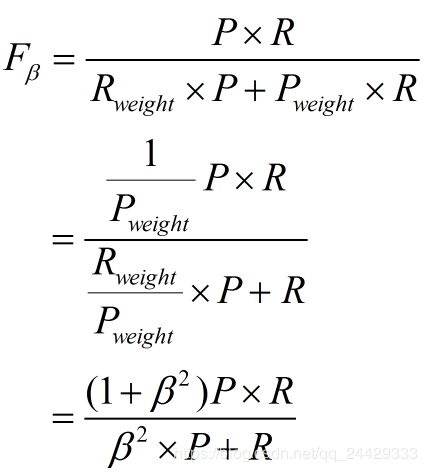机器学习---回归模型和分类模型的评价指标体系

回归模型评价体系

• SSE(误差平方和)：
• R-square(决定系数)
• Adjusted R-square：

分类模型评价体系
一 ROC曲线和AUC值

二 KS曲线

三 GINI系数

四 Lift , Gain

五 模型稳定度指标PSI

1.回归模型评价体系

回归模型的几个评价指标
对于回归模型效果的判断指标经过了几个过程，从SSE到R-square再到Ajusted R-square, 是一个完善的过程：

SSE(误差平方和)：The sum of squares due to error
R-square(决定系数)：Coefficient of determination
Adjusted R-square：Degree-of-freedom adjusted coefficient of determination
下面我对以上几个名词进行详细的解释下，相信能给大家带来一定的帮助！！

2.分类模型评价体系

模型建立之后，必须对模型的效果进行评估，因为数据挖掘是一个探索的过程，评估-优化是一个永恒的过程。在分类模型评估中，最常用的两种评估标准就是KS值和GINI, AUC值.

可能有人会问了，为什么不直接看正确率呢？你可以这么想，如果一批样本中，正样本占到90%，负样本只占10%，那么我即使模型什么也不做，把样本全部判定为正，也能有90%的正确率咯？所以，用AUC值够保证你在样本不均衡的情况下也能准确评估模型的好坏，而KS值不仅能告诉你准确与否，还能告诉你模型对好坏客户是否有足够的区分度。

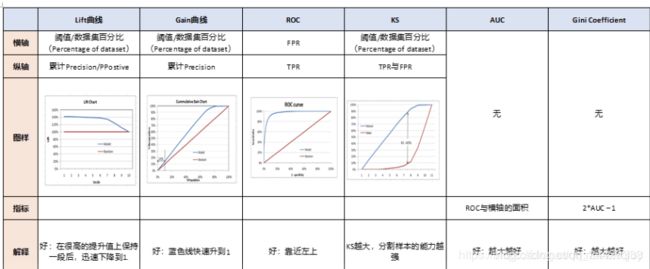
分类模型的评判指标光是图就有好多，ROC，AUC，GINI，KS，Lift，Gain，MSE，这些有些是图有些是指标，放在一起乱七八糟搞得人分不清东南西北。所以这里我先整体给大家一个直观的介绍。省的以后再遇上这么多图的时候完全分不清是谁是谁。
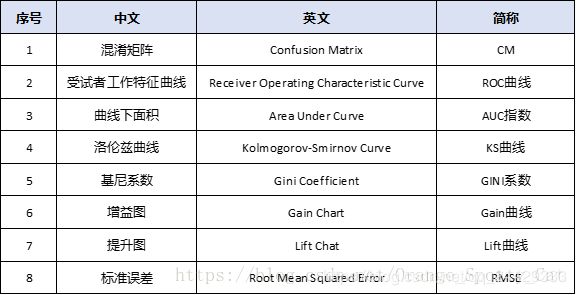
中文，英文，简称
在介绍之前，我们先重新明确一下这些图表的名称，中文、英文、简称，全部来熟悉一下：

三句话概括版本：

Confusion Matrix -> Lift，Gain，ROC。

ROC -> AUC，KS -> GINI。

MSE独立出来。

拟人化概括
其实，这些图之间的关系不是很复杂。我尝试着用一个小故事概括一下8位登场人物之间的关系。

故事是这样的：

首先，混淆矩阵是个元老，年龄最大也资历最老。创建了两个帮派，一个夫妻帮，一个阶级帮。

之后，夫妻帮里面是夫妻两个，一个Lift曲线，一个Gain曲线，两个人不分高低，共用一个横轴。

再次，阶级帮里面就比较混乱。
       1. 帮主是ROC曲线。

       2. 副帮主是KS曲线，AUC面积

       3. AUC养了一个小弟，叫GINI系数。

最后，MSE是世外高人，游离在整个帮派系统之外。

好了，现在咱们应该比较清楚谁跟谁关系好，哪些曲线指标应该抱成一团儿了吧。

原文：https://blog.csdn.net/Orange_Spotty_Cat/article/details/82425113

记住这个之后，我们来理解一下他们之间的关系。

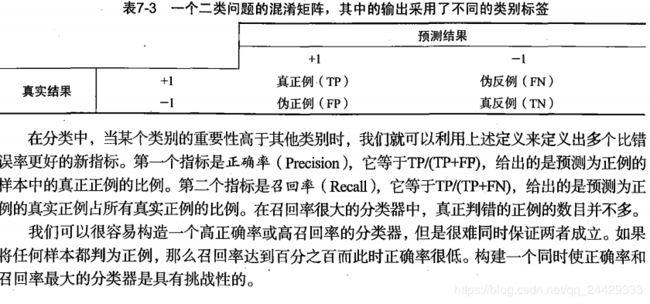
2.1， 混淆矩阵—Confision matrix

TP（实际为正预测为正），FP（实际为负但预测为正），TN（实际为负预测为负），FN（实际为正但预测为负）

• 查全率（召回率，recall）：
  样本中的正例有多少被预测准确了，衡量的是查全率，预测对的正例数占真正的正例数的比率：

  查全率＝检索出的相关信息量 / 系统中的相关信息总量 = TP / (TP+FN)

• 查准率（精准率，Precision）

针对预测结果而言，预测为正的样本有多少是真正的正样本，衡量的是查准率，预测正确的正例数占预测为正例总量的比率：
查准率＝正确预测到的正例数/实际正例总数 = TP / (TP+FP)

• 准确率：反映分类器统对整个样本的判定能力，能将正的判定为正，负的判定为负的能力，计算公式
  Accuracy=(TP+TN) / (TP+FP+TN+FN)

• 阴性预测值：可以理解为负样本的查准率，阴性预测值被预测准确的比例，计算公式：
  NPV=正确预测到的负例数/实际负例总数=TN / (TN+FN)

查准率和查全率通常是一对矛盾的度量，通常一个高，另外一个就低。两个指标都很重要，我们应该如何综合考虑这两个指标呢？
主要有两种办法

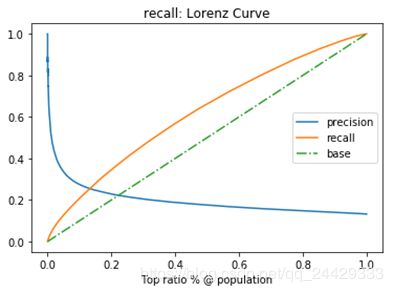
1. "平衡点“ Break-Even Point, BEP
   查准率=查全率的点，过了这个点，查全率将增加，查准率将降低。如下图，蓝色和橘黄色的交叉点就是“平衡点”
   
2. F1度量—查准率和查全率的加权调和平均数
   （1）当认为查准率和查全率一样重要时，权重相同时：（1）当认为查准率和查全率一样重要时，权重相同时：
   这个2应该没有

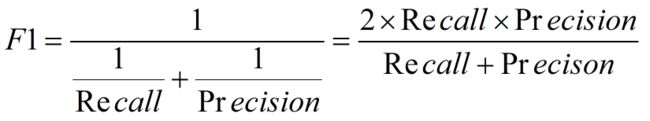
（2）当查准率查全率的重要性不同时，即权重不同时：
通常，对于不同的问题，查准率查全率的侧重不同。比如，对于商品推荐系统，为了减少对用户的干扰，查准率更重要；逃犯系统中，查全率更重要。因此，F1度量的一般形式：

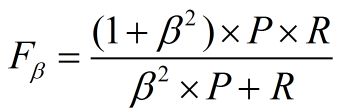
其中β表示查全率与查准率的权重，很多参考书上就只给出了这个公式，那么究竟怎么推导来的呢？
两个指标的设置及其关系如下，因为只考虑这两个指标，所以二者权重和为1，即

可以推导得到

带权重的调和平均数公式如下


因此

1. β=1，查全率的权重=查准率的权重，就是F1
2. β>1，查全率的权重>查准率的权重
3. β<1，查全率的权重<查准率的权重

那么问题又来了，如果说我们有多个二分类混淆矩阵，应该怎么评价F1指标呢？
多个二分类混淆矩阵可能有以下几种情况：多次训练/测试，多个数据集上进行训练/测试，多分类任务的两两类别组合等
这里介绍两种做法：

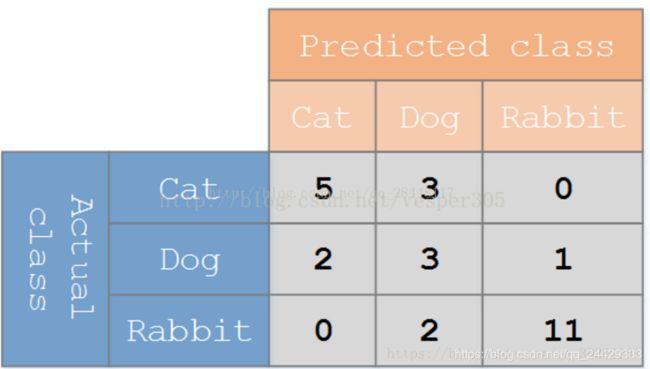
假设有一个用来对猫（cats）、狗（dogs）、兔子（rabbits）进行分类的系统，混淆矩阵就是为了进一步分析性能而对该算法测试结果做出的总结。假设总共有
27 只动物：8只猫， 6条狗， 13只兔子。结果的混淆矩阵如上图：

在这个混淆矩阵中，实际有8只猫，但是系统将其中3只预测成了狗；对于6条狗，其中有1条被预测成了兔子，2条被预测成了猫。从混淆矩阵中我们可以看出系统对于区分猫和狗存在一些问题，但是区分兔子和其他动物的效果还是不错的。所有正确的预测结果都在对角线上，所以从混淆矩阵中可以很方便直观的看出哪里有错误，因为他们呈现在对角线外面。
在预测分析中，混淆表格（有时候也称为混淆矩阵），是由false positives，falsenegatives，true positives和true negatives组成的两行两列的表格。它允许我们做出更多的分析，而不仅仅是局限在正确率，对于上面的矩阵，可以表示为下面的表格：

（1）宏F1
设有n个混淆矩阵，计算出查全率和查准率的平均值，在计算F1即可，这种做法认为每一次的混淆矩阵（训练）是同等权重的

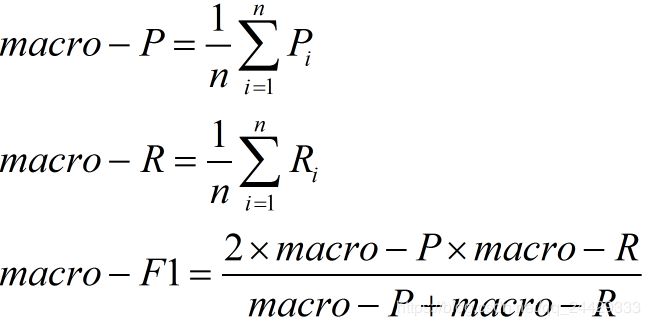
（2）微F1
设有n个混淆矩阵，计算出混淆矩阵对应元素（TP，FP，FN，TN）的平均值，再计算查全率、查准率，F1

这种做法认为每一个样本的权重是一样的

分类器产生的结果通常是一个概率值不是直接的0/1变量，通常数值越到，代表正例的可能性越大。
根据任务的不同也会采取不同的“截断点”，大于则为正例，小于则为反例。如重视查全率，则阈值可以设置低一些；而重视查准率，阈值可以设置高一些。
如果设定了截断点或明确了任务，那么我们根据混淆矩阵就可以知道分类器的效果好坏。

2.2 ROC曲线， AUC ----评价学习器性能，检验分类器对客户进行正确排序的能力

但是在未设定截断点（任务不明确）情况下，我们如何评价一个分类模型的效果的好坏或者比较不同分类模型效果？
我们可以观察这个学习器利用所有可能的截断点（就是所有样本的预测结果）对样本进行分类时的效果，注意要先对所有可能的截断点进行排序，方便对比观察。

ROC曲线描绘的是不同的截断点时，并以FPR和TPR为横纵坐标轴，描述随着截断点的变小，TPR随着FPR的变化。
纵轴：TPR=正例分对的概率 = TP/(TP+FN)，其实就是查全率
横轴：FPR=负例分错的概率 = FP/(FP+TN) 0–错误预测率

如果是随机分类，没有进行任何学习器，FPR=TPR，即正例分对和负例分错概率相同，预测出来的正例负例和正例负例本身的分布是一致的，所以是一条45°的直线。因此，ROC曲线越向上远离这条45°直线，说明用了这个学习器在很小的代价（负例分错为正例，横轴）下达到了相对较大的查全率（TPR）

作图步骤：

1. 根据学习器的预测结果（注意，是正例的概率值，非0/1变量）对样本进行排序（从大到小）-----这就是截断点依次选取的顺序
2. 按顺序选取截断点，并计算TPR和FPR—也可以只选取n个截断点，分别在1/n，2/n，3/n等位置
3. 连接所有的点（TPR，FPR）即为ROC图

例图：因为样本有限，通常不是平滑曲线

可以看到，TPR也就是我们所说的召回率，那么只要给定一个决策边界阈值t，我们可以得到一个对应的TPR和FPR值，然而，我们不从这个思路来简单的得到TPR和FPR，而是反过来得到对应的t，我们检测大量的阈值clip_image002[7]，从而可以得到一个TPR-FPR的相关图，如下图所示
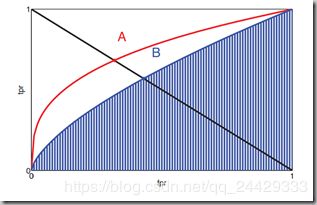
图中的红色曲线和蓝色曲线分别表示了两个不同的分类器的TPR-FPR曲线，曲线上的任意一点都对应了一个阈值。该曲线就是ROC曲线（receiver operating characteristic curve）。

该曲线具有以下特征：

一定经过（0,0）点，此时t，没有预测为P的值，TP和FP都为0
一定经过（1,1）点，此时t，全都预测为P
最完美的分类器（完全区分正负样例）：（0,1）点，即没有FP，全是TP
曲线越是“凸”向左上角，说明分类器效果越好
随机预测会得到（0,0）和（1,1）的直线上的一个点 曲线上离（0,1）越近的点分类效果越好，对应着越合理的t
从图中可以看出，红色曲线所代表的分类器效果好于蓝色曲线所表示的分类器

判断标准：

1. 一个ROC曲线完全”包住“另一个ROC曲线—>第一个学习器效果更好
2. 两个ROC曲线相交—>利用ROC曲线下的面积（AUC，area under ROC curve，是一个数值)进行比较
   利用ROC的其他评估标准
   AUC(area under thecurve)，也就是ROC曲线的下夹面积，越大说明分类器越好，最大值是1，图中的蓝色条纹区域面积就是蓝色曲线对应的 AUC
   而AUC比这三者更为常用。因为一般在分类模型中，预测结果都是以概率的形式表现，如果要计算准确率，通常都会手动设置一个阈值来将对应的概率转化成类别，这个阈值也就很大程度上影响了模型准确率的计算。AUC能很好描述模型整体性能的高低。从一定程度上讲,它可以描述预测结果中正例排在负例前面的概率。

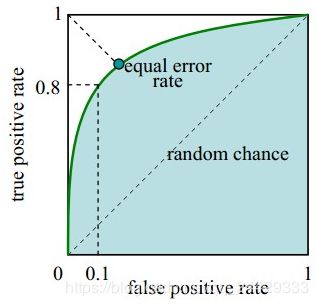
EER（equal error rate），也就是FPR=FNR的值，由于FNR=1-TPR，可以画一条从（0,1）到（1,0）的直线，找到交点，图中的A、B两点。EER是（一个分类器的）ROC曲线（接受者操作特性曲线）中错分正负样本概率相等的点（所对应的错分概率值）。这个点就是ROC曲线与ROC空间中对角线（[0,1]-[1,0]连线）的交点.RR 是 Bayesian决策中最佳阈值对应的错误率，此时False acceptance 和 False rejection是相等的，
ERR可以用来衡量算法的错误率，ERR越小表示算法错误率越低

ROC曲线有个很好的特性：当测试集中的正负样本的分布变换的时候，ROC曲线能够保持不变。在实际的数据集中经常会出现样本类不平衡，即正负样本比例差距较大，而且测试数据中的正负样本也可能随着时间变化

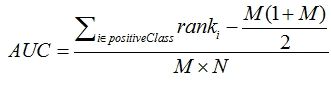
所有的 M×N(M为正类样本的数目，N为负类样本的数目)个正负样本对中, 它也是首先对score从大到小排序，然后令最大score对应的sample 的rank为n，第二大score对应sample的rank为n-1，以此类推。然后把所有的正类样本的rank相加，再减去M-1种两个正样本组合的情况。得到的就是所有的样本中有多少对正类样本的score大于负类样本的score。然后再除以M×N

3. KS曲线，和Gini系数

KS值—学习器将正例和反例分开的能力，确定最好的“截断点” KS曲线和ROC曲线都用到了TPR，FPR。KS曲线是把TPR和FPR都作为纵坐标，而样本数作为横坐标。KS值—学习器将正例和反例分开的能力，确定最好的“截断点” KS曲线和ROC曲线都用到了TPR，FPR。KS曲线是把TPR和FPR都作为纵坐标，而样本数作为横坐标。

作图步骤：

1. 根据学习器的预测结果（注意，是正例的概率值，非0/1变量）对样本进行排序（从大到小）-----这就是截断点依次选取的顺序
2. 按顺序选取截断点，并计算TPR和FPR —也可以只选取n个截断点，分别在1/n，2/n，3/n等位置
3. 横轴为样本的占比百分比（最大100%），纵轴分别为TPR和FPR，可以得到KS曲线
4. TPR和FPR曲线分隔最开的位置就是最好的”截断点“，最大间隔距离就是KS值，通常>0.2即可认为模型有比较好偶的预测准确性
   例图：
   
   风控分类模型种类（决策、排序）比较与模型评估体系（ROC/gini/KS/lift）
   区分度指标（KS）是度量具体模型下正常样本和违约样本分布的最大差距，首先按照样本的信用分数或预测违约率从小到大进行排序，然后计算每一个分数或违约率下好坏样本的累计占比。正常和违约样本的累计占比差值的最大值即为区分度指标（KS）。区分度指标（KS）的示意如图2所示。区分度指标（KS）小于0.2代表模型准确性差，超过0.75则代表模型准确性高。

实际上是就是你建立好模型后，按照评分从大到小排列后：检验你所谓的好客户和坏客户两类客户分布的差异性，即模型区分度。分布根据好坏两个客户评分的累积密度分布曲线，画出来的：比如好坏客户共100个，按照评分排序后前百分之十的客户即10个，其中好的客户有8个，坏的客户有2个（总体样本中好客户80个，坏客户20个），那么前10%的客户的累积密度为：好客户10%，坏客户10%。同理前20%的客户中其中好的客户有15个，坏的客户有5个那么前20%的客户的累积密度为：好客户18.75%，坏客户25%
以此类推可以得出前30%，40%。。。。100%的累积密度。以10%，20%，30%。。。100%为横坐标，以两类客户累积密度为纵坐标，即可画出KS曲线图。

KS值表示了模型将+和-区分开来的能力。值越大，模型的预测准确性越好。一般，KS>0.2即可认为模型有比较好的预测准确性。
KS值一般是很难达到0.6的，在0.2~0.6之间都不错。一般如果是如果负样本对业务影响极大，那么区分度肯定就很重要，此时K-S比AUC更合适用作模型评估，如果没什么特别的影响，那么用AUC就很好了。
笔记︱风控分类模型种类（决策、排序）比较与模型评估体系（ROC/gini/KS/lift）
https://blog.csdn.net/sinat_26917383/article/details/51725102
GINI系数:也是用于模型风险区分能力进行评估。
GINI统计值衡量坏账户数在好账户数上的的累积分布与随机分布曲线之间的面积，好账户与坏账户分布之间的差异越大，GINI指标越高，表明模型的风险区分能力越强。

GINI系数的计算步骤如下：

1. 计算每个评分区间的好坏账户数。
2. 计算每个评分区间的累计好账户数占总好账户数比率（累计good%）和累计坏账户数占总坏账户数比率(累计bad%)。
3. 按照累计好账户占比和累计坏账户占比得出下图所示曲线ADC。
4. 计算出图中阴影部分面积，阴影面积占直角三角形ABC面积的百分比，即为GINI系数。

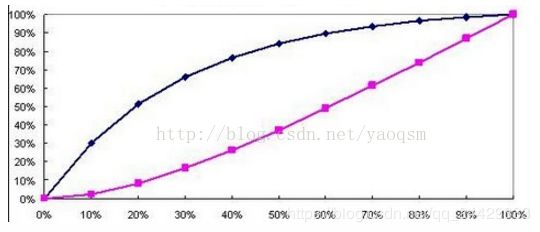
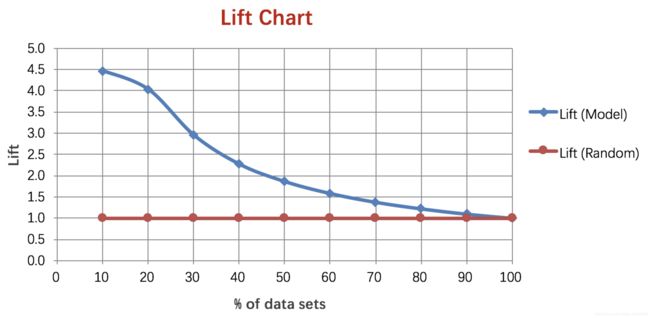
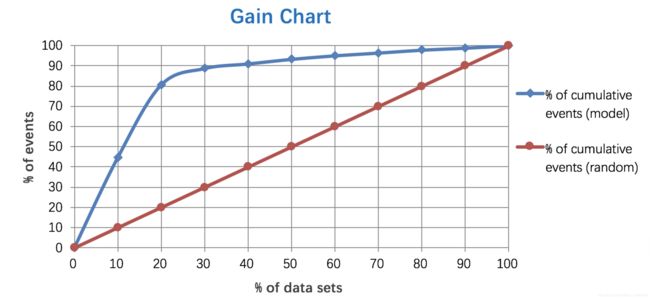
4. Lift 和Gain图

*个人认为前三个指标应用场景更多一些。
Lift图衡量的是，与不利用模型相比，模型的预测能力“变好”了多少，lift(提升指数)越大，模型的运行效果越好。
Gain图是描述整体精准度的指标。 和查准率一样

*
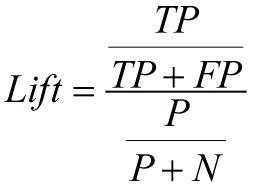
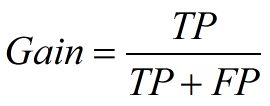
作图步骤：

1. 根据学习器的预测结果（注意，是正例的概率值，非0/1变量）对样本进行排序（从大到小）-----这就是截断点依次选取的顺序
2. 按顺序选取截断点，并计算Lift和Gain —也可以只选取n个截断点，分别在1/n，2/n，3/n等位置
   例图：
   
   

模型稳定度指标PSI

群体稳定性指标PSI(Population Stability Index)是衡量模型的预测值与实际值偏差大小的指标。

PSI = sum（（实际占比-预期占比）* ln（实际占比/预期占比））

举例：

比如训练一个logistic回归模型，预测时候会有个概率输出p。
测试集上的输出设定为p1吧，将它从小到大排序后10等分，如0-0.1,0.1-0.2,…。
现在用这个模型去对新的样本进行预测，预测结果叫p2，按p1的区间也划分为10等分。
实际占比就是p2上在各区间的用户占比，预期占比就是p1上各区间的用户占比。
意义就是如果模型跟稳定，那么p1和p2上各区间的用户应该是相近的，占比不会变动很大，也就是预测出来的概率不会差距很大。

一般认为PSI小于0.1时候模型稳定性很高，0.1-0.25一般，大于0.25模型稳定性差，建议重做。

PS：除了按概率值大小等距十等分外，还可以对概率排序后按数量十等分，两种方法计算得到的psi可能有所区别但数值相差不大。

原文：https://blog.csdn.net/zwqjoy/article/details/84859405

https://blog.csdn.net/shy19890510/article/details/79501582
https://blog.csdn.net/Orange_Spotty_Cat/article/details/82425113